mientos uniformes que, por impulsiones sucesivas, se producen unos a otros. Representémonos de nuevo nuestra mesa y establezcamos que la bola debe recibir a cada brevísimo tiempo t, un choque de la misma cantidad y dirección (fig. 26). Si la bola parte del punto o con una velocidad inicial cualquiera, llegará en t sec. a un punto 1, en donde le alcanza el primer choque; de aquí corre en otra dirección con otra velocidad, durante t sec, hasta que en el punto 2 recibe un nuevo choque que la desvía, etc. Cada una de las desviaciones es determinable por la ley de impulsión; por lo tanto, puede construirse todo el proceso del movimiento y se ve que el punto de partida, la dirección inicial y la velocidad inicial determinan enteramente el posterior curso. En este movimiento de retroceso tenemos una imagen grosera del movimiento de una bola sobre un plano inclinado; y la imagen coincidirá tanto mejor con el proceso, en realidad continuo, cuanto más pequeño sea el intervalo de tiempo que se haya elegido entre los choques.
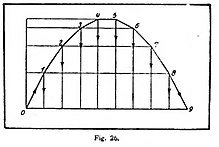
Lo que aquí se ha conseguido por construcción lo realiza el cálculo integral en el caso de fuerzas continuamente activas. También aquí permanecen enteramente arbitrarios el punto de partida y la velocidad inicial en cantidad y dirección; pero si éstos son dados, queda perfectamente determinado el ulterior curso del movimiento. Una y la misma ley de fuerza puede, pues, producir infinitos movimientos, según la elección de las condiciones iniciales; así, la inmensa muchedumbre de los movimientos de caída y de proyección dependen todos de una y

