métricas, y expresarlo todo en las palabras del lenguaje corriente; pero el libro resultaría entonces tan voluminoso y falto de claridad, que no habría editor que lo imprimiese ni lector que lo estudiase.
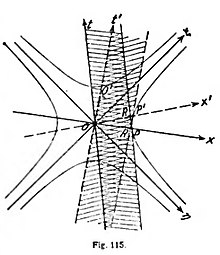
Emplearemos primero nuestra figura en el plano xt, para resolver el problema de determinar la longitud de la vara en los dos sistemas S y S' (fig. 115).
La vara está inmóvil en el sistema S(x, t); por lo cual la línea universal de su punto inicial es el eje t, y la de su punto terminal, la paralela a aquélla a la distancia 1; ésta toca a la curva en el punto P. La vara queda, pues, representada, para todos los tiempos, por la franja entre esas dos rectas.
Ahora debemos determinar su longitud en el sistema S'(x't'), que se mueve con respecto a S; el eje t' está inclinado con respecto al eje t. Encontramos el correspondiente eje x', trazando, por el punto Q' de intersección entre el eje t' y la curva, la tangente a ésta, y por el punto O la paralela a esta tangente, OP'. La distancia OP' es la unidad de longitud en el eje x'. La longitud de la vara unidad, que se halla en reposo en el sistema S, es determinada, si se mide en el sistema S', por la distancia OR', que, en la franja de paralelas representante de la vara, recorta el eje x'; pero esta distancia es evidentemente más corta que OP' y, por lo tanto, es OR' más pequeño que 1: la vara aparece disminuida en el sistema S' en movimiento.
Es ésta exactamente la contracción ideada por Fitz-Gerald y Lorentz para explicar el experimento de Michelson,

