Página:La teoría de la relatividad de Einstein.djvu/68

---

60

La teoría de la relatividad de Einstein.

---

cantidad cualquiera que depende del movimiento y varia de momento en momento. En un pequeño espacio de tiempo t, la cantidad E varia en e; entonces habremos de decir que la relación ${\tfrac {e}{t}}$ es la velocidad de variación de E, y al hacerlo, desde luego pensamos que el espacio de tiempo t debe tomarse siempre lo más pequeño posible—como antes hicimos al definir la velocidad v y la aceleración b—. Si la cantidad E no cambia en el tiempo, es naturalmente su velocidad de variación cero, e inversamente. Ahora vamos a calcular la variación de la expresión anterior E en el tiempo t; durante este tiempo la altura de la caída x disminuye de vt y la velocidad v aumenta de w= bt. Por lo cual E una vez transcurrido el tiempo t, tendrá el valor de

$E'={\frac {m}{2}}(v+w)^{2}+G(x-vt)$.

fig30

Pero sabemos que

$(v+w)^{2}=v^{2}+w^{2}+2vw$

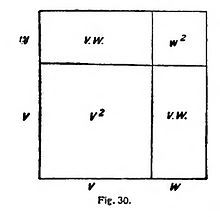
lo cual quiere decir que el cuadrado levantado sobre las dos distancias sucesivas v y w puede dividirse en un cuadrado cuyo lado sea v, en otro cuyo lado sea w y en dos rectángulos iguales cuyos lados sean v y w (figura 30).

Por donde resulta:

$E'={\frac {m}{2}}v^{2}+{\frac {m}{2}}w^{2}+mvw+Gx-Gvt$

Si se substrae ahora el antiguo valor de E, tendremos como variación

$e=E'-E={\frac {m}{2}}w^{2}+mvw-Gvt$,