Almagesto: Libro XII - Capítulo 03
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
{Demostración de los [Movimientos] Retrógrados de Júpiter}
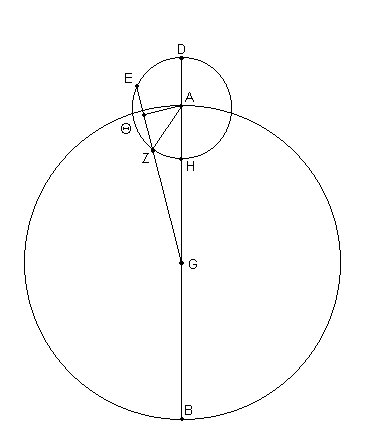
Para Júpiter [ver Fig. 12.9], de acuerdo a nuestros cálculos, para la distancia media,
ΘZ / GZ = 1 / 10;51,29 [1],
y EG / ZG = 12;51,29 / 10;51,29,
entonces EG * ZG = 139;37,39 [2].
Además GA / AD = 60 / 11;30
y GD / GH = 71;30 / 48;30,
entonces GD * GH = 3467;45.
Dividiendo [3467;45 por 139;37,39] tenemos 24;50,9, cuya raíz cuadrada [es], 4;59,1, [valor que lo] multiplicamos por la proporción anterior de ΘZ / GZ, y tomamos, en términos de los tamaños dados de GA y AZ [por ej. 60 y 11;30],
ΘZ = 4;59,1p
y GZ = 54;6,44p en las mismas unidades,
y, por suma, GΘ = 59;5,45p.
Por consiguiente, expresado en unidades donde las hipotenusas AZ y AG son de 120p [respectivamente].
ΘZ = 52;0,10p
y GΘ = 118;11,30p,
y los arcos correspondientes [3] son:
arco ZΘ = 51;21,41º
y arco GΘ = 160;4,55º.
Por consiguiente calculamos el ^ ZAΘ ≈ 25;40,50º
y el ^ GAΘ ≈ 80;2,28º,
y, por sustracción [del ^ GAΘ de los 90º], el ^ ZGA, que representa el [Movimiento] Retrógrado debido a la velocidad del planeta, es de 9;57,32º, el ^ ZAH, que representa el [movimiento] aparente en anomalía, es de [^ GAΘ - ^ ZAΘ =] 54;21,38º. A esto último le corresponden 5;1,24º en movimiento longitudinal, de acuerdo a la proporción de arriba [de 1 / 10;51,29] [4]. Así
| la mitad del [movimiento] retrógrado es de | 4;56,8º y alrededor de 60 ½ días, |
| y el [movimiento] retrógrado total es de | 9;52,16º y 121 días. |
La distancia en una Elongación de alrededor de 5º desde el apogeo o desde el perigeo [respectivamente] es insignificantemente más pequeña que la máxima distancia e insignificantemente mayor que la mínima distancia.
De acuerdo a nuestros cálculos, para la máxima distancia, la ecuación [correspondiente a 1º] para la corrección [de las velocidades] es de 5 ⅙ minutos [5]. Por lo tanto
ΘZ / GZ = 0;54,50 / 10;56,39
y EG / GZ = 12;46,19 / 10;56,39,
y EG * GZ = 139;46,42.
Además, GA / AD = 62;45 / 11;30,
DG / GH = 74;15 / 51;15,
y DG * GH = 3805;18,45.
Dividiendo [3805;18,45 por 139;46,42], tomamos 27;13,26, cuya raíz cuadrada [es], 5;13,4, cuando multiplicado por la proporción de ΘZ / GZ, da, en términos de los tamaños dados de GA y AZ [por ej. 62;45 y 11;30]
ZΘ = 4;46,6p,
GZ = 57;6,19p [6],
y, por suma, GΘ = 61;52,25p.
Por consiguiente, expresado en unidades donde las hipotenusas AZ y AG son [respectivamente] de 120p,
ZΘ = 49;45,23p
y GΘ = 118;19,27p,
y los arcos correspondientes son:
arco ZΘ = 48;59,34º
arco GΘ = 160;49,36º.
Por consiguiente, el ^ ZAΘ = 24;29,47º
y el ^ GAΘ = 80;24,48º.
Y, por sustracción, el ^ ZGA, que representa el [movimiento] retrógrado debido a la velocidad del planeta, es de [90º - ^ GAΘ =] 9;35,12º, y el ^ ZAH, que representa el [movimiento] aparente en anomalía, es de [^ GAΘ - ^ ZAΘ =] 55;55,1º. A esto último le corresponden 4;40,35º en movimiento longitudinal corregido [7], y 5;6,35° en movimiento medio [longitudinal], de acuerdo a la proporción [de las velocidades] en el apogeo. Por lo tanto
| la mitad del [movimiento] retrógrado es de | [9;35,12º - 4;40,35º =] 4;54,37º y alrededor de 61 ½ días, |
| y el [movimiento] retrógrado total es de | 9;49,14º y 123 días. |
De acuerdo con nuestros cálculos, para la mínima distancia, la ecuación [correspondiente al 1º] para la corrección [de las velocidades] es hallada ser de 5 ⅔ minutos [8]. Por lo tanto
ΘZ / ZG = 1;5,40 / 10;45,49,
EG / GZ = 12;57,9 / 10;45,49,
y EG * ZG = 139;24,56.
Además, GA / AD = 57;15 / 11;30,
DG / GH = 68;45 / 45;45,
y DG * GH = 3145;18,45.
Dividiendo [lo último por 139;24,56], tomamos 22;33,39, cuya raíz cuadrada [es], 4;45, multiplicado por la proporción de arriba de ΘZ / GZ, da, en términos de los tamaños de arriba de GA y AZ [por ej. 57;15 y 11;30],
ΘZ = 5;11,55p,
ZG = 51;7,38p,
y, por suma, GΘ = 56;19,33p.
Por lo tanto, expresado en unidades donde las hipotenusas ZA y AG son [respectivamente] de 120p,
ZΘ = 54;14,47p
y GΘ = 118;3,46p,
y los arcos correspondientes
arco ZΘ = 53;45,4º
y arco GΘ = 159;22,40º.
Por consiguiente el ^ ZAΘ = 26;52,32º
y el ^ GAΘ = 79;41,20º.
Y, por sustracción, el ^ ZGA, que representa el [movimiento] retrógrado debido a la velocidad del planeta, es de [90º - ^ GAΘ =] 10;18,40º, y el ^ ZAH, que representa el [movimiento] aparente en anomalía, es de [^ GAΘ - ^ ZAΘ =] 52;48,48º. A esto último le corresponden 5;21,20º en movimiento longitudinal corregido [9], y 4;54,20º en movimiento medio [longitudinal], de acuerdo a la proporción [de las velocidades] en el perigeo. Por lo tanto
| la mitad del [movimiento] retrógrado es de | [10;18,40º - 5;21,20º =] 4;57,20º y alrededor de 59 días, |
| y el [movimiento] retrógrado total es de | 9;54,40º y 118 días. |
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Libro XII |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 |
Notas de referencia
- ↑ Tomando los tres primeros lugares (redondeados) de los movimientos medios diarios desde Libro IX Capítulo 4 (cf. Libro XII Capítulo 2 nota de referencia nro. 4), uno toma 0;54,9,3 / 0;4,59,14 = 10;51,28,29...
- ↑ Ptolomeo ha cometido un error de cálculo: el [valor] correcto es 139;36,48, e incluso este es hallado en el manuscrito Ger (Gerardo de Cremona), sin dudas derivado del tipo de corrección marginal encontrada en el manuscrito D² (139;36,48,32). Los cálculos posteriores muestran que el error es de Ptolomeo (en H474,5 (en el manuscrito Ger - Gerardo de Cremona - se lee 24;50,17, nuevamente de acuerdo con el manuscrito D² y con la cantidad anterior, aunque la raíz cuadrada debería ser 4;59,2, mientras que en toda la tradición esta de acuerdo con 4;59,1, que es confirmado por los siguientes cálculos).
- ↑ Leer ' en H474,16 (en todos los manuscritos) en cambio de la corrección de Heiberg ' . También el genitivo es normal en el Almagesto en las expresiones del tipo ZΘ , el dativo (nombre y pronombre) después de es perfectamente bien del Griego, y es explicable aquí como para evitar la ambigüedad de los dos plurales genitivos referidos a diferentes cosas. He restaurado las lecturas de los manuscritos en pasajes similares en H476,9 y en H477,18.
- ↑ De hecho 54;21,38 / 10;51,29 = 5;0,23º. Pero el número en el texto esta confirmado por los siguientes cálculos.
- ↑ Leer seg. ' (en los manuscritos L y Ger - Gerardo de Cremona) en H475,14 en cambio de seg. seg. (5;6). La corrección fue hecha por Manitius, quien señala que, en la tabla de la anomalía, para un argumento de 6º le corresponde una Ecuación del Centro de 0;31º, por lo tanto, para 1º, 0;5,10º.
- ↑ Más exacto podría ser 57;6,15, que es la lectura en el manuscrito D y esta dada como una alternativa en los manuscritos A, B y C. Pero el texto esta garantizado por los siguientes cálculos.
- ↑ Cf. Libro XII Capítulo 2, nota de referencia nro. 16. Cálculo: 55;55,1º * 1 / 10;56,39 = 5;6,33º, que le corresponde una ecuación de 0;26,24º ≈ 26'. [Luego] 55;55,1º - 0;26º = 55;29,1º. Esto multiplicado por 1 / 10;51,29 = 5;6,35º [por lo tanto en el texto; [es] exactamente 5;6,36]. [Finalmente] 5;6,35º - 0;26 = 4;40,35º.
- ↑ En la Tabla de la Anomalía, para un argumento de [180º - 3º =] 177º le corresponde una ecuación de 0;17º, por consiguiente para 1º cerca del perigeo le corresponde 5 ⅔'.
- ↑ Libro XII Capítulo 2 nota de referencia nro. 16. Cálculo: 52;48,48º * 1 / 10;45,49 = 4;54,24º, que le corresponde una ecuación de 27' [entonces en el texto: el [valor] preciso podría ser 29']. [Luego] 52;48,48º + 0;27º = 53;15,48º, que multiplicado por 1 / 10;51,29 da 4;54,20º [de manera precisa 4;54,19º]. [Finalmente] 4;54,20º + 0;27º = 5,21,20º.
