Almagesto: Libro XII - Capítulo 02
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
{Demostración de los [Movimientos] Retrógrados de Saturno}
Habiendo establecido lo anterior, seguidamente expondremos los cálculos de los [Movimientos] Retrógrados para cada uno de los planetas, de acuerdo con las hipótesis [previamente] demostradas, [y] comenzando con Saturno. El método es el siguiente.

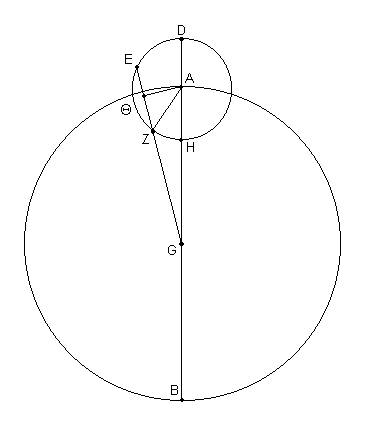
[Ver Fig. 12.6] [1] Sea AB el círculo transportando el centro del Epiciclo sobre el diámetro AGB, sobre el cuál G representa el centro de la Eclíptica, por ej. nuestro punto de vista. Describir el epiciclo DEZH sobre el centro A, y dibujar la línea GZE de tal modo que, cuando la perpendicular AΘ es eliminada sobre él, la proporción de la mitad de EZ (por ej. ΘZ) hasta ZG es aquella de la velocidad del epiciclo sobre la velocidad del planeta. Supongamos, primero, que el epiciclo esta situado en la distancia media: por lo tanto los movimientos medios en longitud y en anomalía son aproximadamente los mismos como las movimientos [en longitud y en anomalía] tomados con respecto al centro de la eclíptica [2].
Ahora para Saturno, como demostramos en el (Libro XI Capítulo 6), donde la distancia media GA es de 60p, el radio del epiciclo AD = 6 ½p.
Así, por adición, DG = 66;30p,
y, por sustracción, GH = 53;30p en las mismas unidades.

En consecuencia su producto [3] es [igual a] 3557;45p.
Pero (DG * GH) = (EG * GZ),
Entonces (EG * GZ) = 3557;45p en las mismas unidades.
Además (de acuerdo con los movimientos medios), donde la velocidad del epiciclo (por ej. ΘZ) es de 1p, la velocidad del planeta (por ej. ZG) es alrededor de 28;25,46p [4].
Por lo tanto, por adición, EG [= ZG + 2 * ΘZ] = 30;25,46p,
y EG * GZ = 865;5,32p en las mismas unidades.
Entonces si dividimos [5] 3557;45 por 865;5,32, que da un cociente de 4;6,45, tomar la raíz cuadrada de esto último, 2;1,40, y multiplicando este factor por ΘZ (= 1p) y por ZG (= 28;25,46p) separadamente, tomamos
ΘZ = 2;1,40p donde (EG * GZ) = 3557;45p
y ZG = 57;38,55p donde (EG * GZ) = 3557;45p.
Por lo tanto si unimos AZ, donde AZ = 6;30p,
ZΘ = 2;1,40p,
entonces donde AZ = 120p, ZΘ = 37;26,9p.
Por lo tanto, en el círculo alrededor del triángulo rectángulo AZΘ,
arco ΘZ = 36;21,15º [6],
Entonces el ^ ZAΘ = 36;21;15ºº donde 2 ángulos rectos = 360ºº
Entonces el ^ ZAΘ ≈ 18;10,38º donde 4 ángulos rectos = 360º.
Además, donde la hipotenusa [del triángulo rectángulo AGΘ] GHA = 60p,
por suma, GZΘ [= 57;38,55p + 2;1,40p] = 59;40,35p,
entonces donde GHA = 120p, GZΘ = 119;21,10p.
Entonces, en el círculo alrededor del triángulo rectángulo AGΘ,
arco GΘ = 168;5,39º.
En consecuencia el ^ GAΘ = 168;5,39ºº donde 2 ángulos rectos = 360ºº
En consecuencia el ^ GAΘ ≈ 84;2,50º donde 4 ángulos rectos = 360º.
Por consiguiente tomamos ^ AGΘ = 5;57,10º (complementario),
y el ^ ZAH = ^ GAΘ - ^ ZAΘ = 65;52,12º.
Entonces, dado que el planeta es observado a lo largo de la línea GZ en la primera [Posición] Estacionaria, y a lo largo de GH en la Oposición [media], esta claro que, si el centro del epiciclo no tuvo un movimiento hacia atrás [durante ese intervalo], el arco ZH del epiciclo, comprendiendo 65;52,12º, podría producir un movimiento retrógrado por la cantidad del ^ AGZ, de 5;57,10º. Pero dado que, de acuerdo con la proporción anterior de la velocidad del epiciclo sobre la velocidad del planeta, esta anomalía de 65;52,12º corresponde aproximadamente en longitud [7] a 2;19º, tomamos un movimiento retrógrado de:
| desde ambas [posiciones] estacionarias hasta la oposición | 3;38,10º y 69 días [8] |
(esto último es aproximadamente el tiempo que toma el planeta en moverse 2;19º en longitud media),
| y un [movimiento] retrógrado total de | 7;16,20º y 138 días. |
Seguidamente investigaremos las cantidades [correspondientes] cerca de la máxima distancia bajo las mismas condiciones, a saber cuando la oposición a mitad de camino entre las [dos posiciones] estacionarias lleva el centro del epiciclo precisamente hasta el apogeo de la Excéntrica, y, obviamente, lleva a cada una de las dos [posiciones] estacionarias hasta una distancia en longitud corregida desde la oposición (por ej. desde el apogeo) [9] que es cercana a los 2;19º [y] que fue derivada [anteriormente] desde la proporción entre los movimientos [medios]. En esta ubicación AG, que representa la distancia en ese momento, es insignificantemente diferente de la máxima distancia [10], y por consiguiente se obtiene vía los teoremas previamente desarrollados, y para 1º de longitud le corresponde una ecuación de alrededor de 6;30' [11]. Por lo tanto la proporción del [movimiento en] longitud corregida sobre el [movimiento en] anomalía corregida, por ej. de la velocidad aparente del epiciclo en ese momento sobre la velocidad aparente del planeta, es de 0;53,30 / 28;32,16 [12].
Luego, repitiendo la misma figura [Fig. 12.7], donde el radio del epiciclo DA es de 6;30p, GA (que es insignificantemente diferente de la máxima distancia) es de 63;25p.
Por consiguiente, por suma, DG es calculada como de 69;55p,
y, por sustracción, GH = 56;55p.
Y DG * GH (= EG * EZ) = 3979;25,25p.
Y, por hipótesis, donde ZΘ (representando la velocidad del epiciclo) es de 0;53,30p, GZ (que representa la velocidad del planeta) es de 28;32,16p;
entonces, por adición, EG [= GZ + 2 * ZΘ] = 30;19,16p,
y EG * GZ = 865;17,50p.
Entonces, nuevamente, dividiendo 3979;25,25 por 865;17,50, que da 4;35,56, [y] tomando la raíz cuadrada de esto último, [nos da] 2;8,40, y multiplicando este factor por ΘZ (= 0;53,30p) y ZG (= 28;32,16p) separadamente, tomamos
ΘZ = 1;54,44p donde AZ = 6;30p y AG = 63;25p
y GZ = 61;11,52p donde AZ = 6;30p y AG = 63;25p.
Y, por suma, GΘ = 63;6,36p en las mismas unidades.
Por lo tanto donde la hipotenusa AZ [del triángulo rectángulo AZΘ] = 120p,
ΘZ = 35;18,9p,
y donde la hipotenusa GA [del triángulo rectángulo AGΘ] = 120p,
GΘ = 119;25,11p.
Por lo tanto, en el círculo alrededor del triángulo rectángulo AZΘ,
arco ΘZ = 34;13,4º,
y, en el círculo alrededor del triángulo rectángulo AGΘ,
arco GΘ = 168;43,38º.
En consecuencia el ^ ZAΘ = 34;13,4ºº donde 2 ángulos rectos = 360ºº
y el ^ GAΘ = 168;43,38ºº donde 2 ángulos rectos = 360ºº.
En consecuencia el ^ ZAΘ = 17;6,32º donde 4 ángulos rectos = 360º
Y el ^ GAΘ = 84;21,49º donde 2 ángulos rectos = 360º.
Por consiguiente, por sustracción [desde los 90º], el ^ AGΘ (que representa la cantidad del [movimiento] retrógrado [13] que allí ocurre en ambas [posiciones] estacionarias y en la oposición, si el epiciclo no tuviera [14] un movimiento hacia adelante) es de 5;38,11º, y, por sustracción [del ^ ZAΘ desde el ^ GAΘ], el ^ ZAH (que representa el movimiento aparente sobre el epiciclo [15] en la misma distancia [inalterable]) es de 67;15,17º.
Ahora, de acuerdo a la proporción de las velocidades en el apogeo, sobre esta última cantidad [67;15,17°] corresponden a 2;6,6º en longitud corregida [16], entonces tomamos,
| para la mitad del [movimiento] retrógrado total | [5;38,11º - 2;6,6º =] 3;32,5º y 70 ⅓ días, |
(esto último es aproximadamente el tiempo que el planeta le toma en recorrer 2;21,25º en longitud media, que es la cantidad correspondiente a los 2;6,6º anteriores en longitud corregida);
| y el [movimiento] retrógrado total es de | 7;4,10° y 140 ⅔ días. |

Nuevamente, investigaremos las cantidades [correspondientes] cerca de la mínima distancia, utilizando la misma figura [Fig. 12.8] y bajo las condiciones similares, por ej. cuando la oposición a medio camino entre [las dos posiciones] estacionarias, esta precisamente en el perigeo de la excéntrica, y ambas [posiciones] estacionarias están en la distancia en longitud anterior [por alrededor de 2;19º] desde la oposición (por ej. desde el perigeo).
En esta situación la distancia AG en este instante, es hallada por el mismo camino [como en la máxima distancia], dado que esta es insignificantemente diferente desde la mínima distancia.
Y para 1º de longitud corresponde una ecuación de alrededor de 7;20 minutos [17]. Entonces aquí la velocidad aparente del epiciclo / la velocidad aparente del planeta = 1;7,20 / 28;18,26 [18].
Por consiguiente, donde ΘZ= 1;7,20p, GZ = 28;18,26p,
y, por suma, EG = 30;33,6p [19],
y EG * GZ = 864;49,58p [20].
Pero donde el radio del epiciclo, DA = 6;30p,
AG es de 56;35p (que es insignificantemente diferente de la mínima distancia);
Por consiguiente, por adición, DG = 63;5p,
y, por sustracción, GH = 50;5p,
y DG * GH (= EG * GZ) = 3159;25,25p.
Por lo tanto si, como antes, dividimos 3159;25,25p por 864;49,58p, que da 3;39,12p, tomamos la raíz cuadrada de esto, [siendo igual a] 1;54,41 [21], y multiplicamos separadamente este último factor por ΘZ (= 1;7,20p) y por ZG (= 28;18,26p), tenemos
ΘZ = 2;8,43p
donde el radio del epiciclo, AZ = 6;30p, y la distancia en el momento, AG = 56;35p;
y GZ = 54;6,22p en las mismas unidades.
Por consiguiente, por suma, GΘ = 56;15,5p en las mismas unidades.
Por lo tanto, donde la hipotenusa AZ = 120p, ΘZ = 39;36,18p,
y, donde la hipotenusa GA = 120p, GΘ = 119;17,46p [22].
Por consiguiente, en el círculo alrededor del triángulo AZΘ,
arco ZΘ = 38;32,34º,
Y, en el círculo alrededor del triángulo rectángulo AGΘ,
arco GΘ = 167;34,54º.
En consecuencia el ^ ZAΘ = 38;32,24ºº donde 2 ángulos rectos = 360ºº
y el ^ GAΘ = 167;34,54ºº donde 2 ángulos rectos = 360ºº.
Y el ^ ZAΘ = 19;16,17º donde 4 ángulos rectos = 360º
Y el ^ GAΘ = 83;47,27º donde 4 ángulos rectos = 360º.
Por lo tanto, por sustracción [desde 90º], tomamos el ^ AGΘ, que representa el [movimiento] retrógrado (debido a la velocidad del planeta) entre ambas [posiciones] estacionarias y la oposición, como de 6;12,33º,
y, nuevamente, por sustracción [del ^ ZAΘ desde el ^ GAΘ], el ^ ZAH, que representa el movimiento aparente sobre el epiciclo en la misma distancia [inalterable], como de 64;31,10º.
De acuerdo a la proporción de las velocidades en el perigeo, sobre esta última cantidad corresponden 2;33,28º en longitud corregida [23]. Por consiguiente,
| tomamos la mitad del [movimiento] retrógrado total, | [6;12,33º - 2;33,28º =] 3;39,5º y 68 días |
(esto último es aproximadamente el tiempo que toma el planeta en recorrer, a velocidad media, 2;16,45º, que es la cantidad en longitud media correspondiente a los anteriores 2;33,28º de la longitud corregida).
| [Por consiguiente el movimiento] retrógrado total es de | 7;18,10º y 136 días |
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Libro XII |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 |
Notas de referencia
- ↑ Ptolomeo utiliza una figura idéntica simplificada (Figs. 12.6 - 12.12), en la que el observador, G, esta representado, para todas las ubicaciones, en el centro del círculo. La actual ubicación esta descrita en la Fig. Q (copiada de Manitius), donde los subíndices 1, 2 y 3 representan las ubicaciones en la distancia media, máxima y mínima respectivamente.
- ↑ Por ej. dado que el centro del epiciclo esta a la misma distancia desde el observador como lo podría estar en el modelo simple tratado en el capítulo 1 (de este libro), uno puede asimilar la ubicación para este, y utilizar los movimientos medios sin modificar. Como Ptolomeo dice, esto involucra una aproximación, ya que el centro del movimiento no es el observador, sino el punto de la Ecuante. Sin embargo, para pequeñas excentricidades esto es insignificante.
- ↑ Literalmente "el rectángulo contenido por ellas".
- ↑ Tomando los movimientos medios diarios tabulados en Libro IX Capítulo 4 uno encuentra la proporción de la longitud sobre la anomalía como de 1 / 28;25,55... Ptolomeo pudo haber tomado [estos] números redondeados 0;57,7,43º/d y 0;2,0,34º/d, que dan lugar a 28;25,48.
- ↑ , literalmente "medirlo colocándolo junto a".
- ↑ Precisamente, 36;21,20º.
- ↑ 65;52,12 / 28;25,46 = 2;19,1.
- ↑ 5;57,10º - 2;19º = 3;38,10º. En 69 días el planeta se ha movido en longitud 2;18,39º, por ej. aquí (y durante toda [la demostración]) Ptolomeo lo redondea muy próximo al día o a la fracción conveniente de un día.
- ↑ Dado que este debe ser el significado, uno tiene que corregir la puntuación de Heiberg en H468,3, eliminando la coma después de , e insertando una coma después de .
- ↑ Dado que el centro del epiciclo esta en el apogeo de la excéntrica a mitad de camino entre las [posiciones] estacionarias, en la actual [posición] estacionaria el epiciclo esta un poco antes o un poco después del apogeo: por lo tanto "insignificantemente diferente".
- ↑ En la tabla de la Anomalía para Saturno (Libro XI Capítulo 11), para los 6º corresponde una Ecuación del Centro de 39': por consiguiente para 1' corresponde exactamente 6 ½'.
- ↑ Por ej. 1º - 0;6,30º y 28;25,46º + 0;6,30º (cf. nota de referencia anterior nro. 4). Ver HAMA 193-4 sobre la justificación de este procedimiento.
- ↑ Leer (en los manuscritos C² y D) en cambio de en H470,6. Cf. H473,1. Corregido por Manitius.
- ↑ Leer en H470,8 reemplazándolo por . No hay autoridad (firmeza) en el manuscrito para mi corrección, aunque es necesaria para este sentido. Como consecuencia de la corrupción de en cambio de justamente arriba, se asumió que fue conectado con , por consiguiente fue cambiado a de acuerdo con él.
- ↑ Por "movimiento aparente" Ptolomeo da a entender "contado desde el perigeo epicíclico verdadero [y no desde el medio]".
- ↑ Uno podría suponer a partir de lo que él dice aquí que Ptolomeo calcula (67;15,17º * 0;53,30) / 28;32,16. Este [cálculo] deriva a 2;6,5º. El presente método de cálculo es explicado al final del Libro XII Capítulo 6 (Fig. R). Siendo el siguiente: (67;15,17º * 1) / 28;32,16 = 2;21,24º. Para esto último corresponde una ecuación de 0;15,19º, que, sustraída desde los 67;15,17º, nos da alrededor de 67º. Entonces (67º * 1) / 28;25,46 = 2;21,25º. 2;21,25º - 0;15,19º = 2;6,6º.
- ↑ Para un argumento de 177º (= 180º - 3º) corresponde una Ecuación del Centro de 0;22º (Tabla Libro XI Capítulo 11). Por consiguiente 1º cerca del perigeo corresponde 0;7,20º.
- ↑ Por ej. 1 + 0;7,20 y 28;25,46 - 0;7,20.
- ↑ Eliminar en H471,18-19 (en los manuscritos D y Ar).
- ↑ Leer seg. en cambio de seg. (error de impresión en Heiberg) en H471,20.
- ↑ Leer seg. en H462,5 en cambio de seg. (1;54,42). Lo último no tiene autoridad (firmeza) en el manuscrito, aunque es la corrección de Heiberg para seg. (45) o para seg. (49) en los manuscritos Griegos. '41' es la lectura del manuscrito de Ger (Gerardo de Cremona) (en todos los otros manuscritos Árabes que he visto tienen '49'), y es demostrado ser el correcto no solo porque es la raíz cuadrada de 3;39,12 (con una precisión a dos lugares sexagesimales = 1;54,40.93), sino porque (más abajo) 1;54,41 * 28;18,26 ≈ 54;6,22 (de acuerdo con el texto), considerando 1;54,42 * 28;18,26 ≈ 54;6,50.
- ↑ 119;17,45p podría ser un resultado más exacto, y corresponde mejor al arco de 167;34,54º dado más abajo. Pero en la ausencia de alguna autoridad del manuscrito, insisto en cambiarlo.
- ↑ Cf. nota de referencia anterior nro. 16. Cálculos de: 64;31,10º * 1 / 28;18,26 = 2;16,45º. Ecuación para 180º - 2;16,45º es 0;16,43º * 64;31,10º + 0;16;43º = 64;47,53º. Lo último multiplicado por 1 / 28;25,46 da 2;16,45º, y 2;16,45 + 0;16,43 = 2;33,28º.
