Almagesto: Libro XII - Capítulo 01
| Ir al Libro XI - Capítulo 12 | Contenidos | Capítulo Siguiente |
{Sobre las preliminares para los [Movimientos] Retrógrados}
Ahora que hemos demostrado lo anterior, la secuela apropiada sería examinar los [movimientos] retrógrados máximos y mínimos asociados con cada uno de los 5 planetas, y demostrar que los tamaños de esos, [calculados] desde las hipótesis anteriormente [descritas], se encuentren en tan estrecho acuerdo como fuera posible con aquellos hallados [a partir] de las observaciones.
En la determinación de este tipo de problema, hay un Lema preliminar (para una única anomalía, que se relaciona con el Sol) demostrado por un número de matemáticos, en particular por Apolonio de Perge, en los siguientes términos.
[1] Si [la anomalía sinódica] esta representada por la Hipótesis del Epiciclo, en la que el Epiciclo realiza el movimiento [medio] en longitud sobre el círculo concéntrico con la Eclíptica hacia atrás [por ej. en el orden] de los signos, y el planeta realiza [uniformemente] el movimiento en anomalía sobre el epiciclo con respecto a su centro, hacia atrás a lo largo del arco cerca del apogeo, y si una línea es dibujada desde nuestro punto de vista intersecando el epiciclo en tal sentido que la proporción de la mitad de este segmento de la línea interceptada dentro del epiciclo hasta el segmento interceptado entre el observador y el punto donde la línea interseca el epiciclo más cercano a su perigeo es igual a la proporción de la velocidad del epiciclo sobre la velocidad del planeta, entonces el punto sobre el arco del epiciclo más cerca del perigeo determinado por la línea entonces dibujada es el límite entre el Movimiento hacia Adelante [Directo] y el [Movimiento] Retrógrado, así que cuando el planeta alcanza este punto crea la apariencia de Estacionario.
[2] Si la anomalía relacionada con el Sol esta representada por la Hipótesis de la Excéntrica (que es una hipótesis viable solo para los tres planetas [exteriores] los cuales pueden alcanzar alguna elongación desde el Sol) [2], en la que el centro de la Excéntrica se mueve [uniformemente] alrededor del centro de la eclíptica con la velocidad media del Sol hacia atrás [por ej. en orden] de los signos, mientras los planetas se mueven sobre la excéntrica hacia adelante [por ej. en el orden inverso] de los signos con una velocidad [uniforme] con respecto al centro de la excéntrica e igual al movimiento [medio] en anomalía, y si una línea es dibujada en la excéntrica a través del centro de la eclíptica (por ej. del observador) en tal sentido que la proporción de la mitad de toda la línea sobre el más pequeño de los dos segmentos de la línea formada por [la posición del] observador es igual a la proporción de la velocidad de la excéntrica sobre la velocidad del planeta, entonces, cuando el planeta llega al punto en el que la línea anterior corta el arco de la excéntrica cerca del perigeo, [se] producirá la apariencia de estacionario.
También conseguimos el resultado requerido por un método el cual, pensado resumidamente, es sin embargo el más conveniente: empleamos una demostración que contiene ambas hipótesis combinadas en una [figura en] común, para demostrar también su conformidad y similitud en esas propias proporciones [3].
Sea ABGD [Fig. 12.1] el epiciclo sobre el centro E y diámetro AEG, que esta prolongado hasta Z, el centro de la eclíptica (por ej. nuestro punto de vista). Cortar arcos iguales, GH, GΘ, a ambos lados del perigeo G, y dibujar ZHB y ZΘD desde Z a través de los punto H y Θ. Unir DH y BΘ hasta intersectarse (cortarse) uno con el otro en el punto K, que se ubicará, obviamente, sobre el diámetro AG.
Decimos, primero, que
AZ / ZG = AK / KG.
[Demostración:] Unir AD, DG, y dibujar LGM a través de G paralelo a AD. Entonces LGM será, obviamente, perpendicular a DG (dado que el ^ ADG es recto).
Entonces, dado que el ^ GDH = ^ GDΘ [en arcos iguales, Euclides III 27,]
GL = GM [en triángulos congruentes LDG y MDG].

En consecuencia AD / GL = AD / GM.
Pero AD / GM = AZ / ZG [triángulo ADZ ||| triángulo GMZ]
y AD / LG = AK / KG [triángulo ADK ||| triángulo GLK].
En consecuencia AZ / ZG = AK / KG.
Así que, si imaginamos el epiciclo ABGD como la actual excéntrica en la Hipótesis de la Excéntrica, el punto K será el centro de la eclíptica, y el diámetro AG estará dividido por él por la misma proporción como [las cantidades correspondientes] en la Hipótesis Epicíclica. Para ello hemos demostrado que la proporción de la máxima distancia AZ en la hipótesis epicíclica, sobre la mínima distancia ZG, es la misma como la [proporción] de la máxima distancia AK en la [hipótesis de la] excéntrica, sobre la mínima distancia, KG.
[Segundo], también decimos que
DZ / ZΘ = BK / KΘ.
[Demostración:] En el diagrama similar [Fig. 12.2] unir la línea BND (obviamente, será perpendicular al diámetro AG), y dibujar ΘX paralela a ella [BND] desde Θ. Luego, dado que

BN = ND,
BN / XΘ = ND / XΘ.
Pero ND / XΘ = DZ / ZΘ [triángulo ZND ||| triángulo ZXΘ]
y BN / XΘ = BK / KΘ [triángulo BNK ||| triángulo ΘXK].
En consecuencia DZ / ZΘ = BK / KΘ.
Entonces, componendo,
(DZ + ZΘ) / ZΘ = BΘ / ΘK.
Y, eliminando las perpendiculares EO y EP, y dividendo, [tomamos],
OZ / ZΘ = PΘ / KΘ [4].
Y, dividendo una vez más,
OΘ / ZΘ = PK / KΘ.
Por lo tanto, si, en la Hipótesis de la Epiciclo, DZ es dibujado en tal sentido que la proporción de OΘ sobre ZΘ es igual a la proporción de la velocidad del epiciclo sobre la velocidad del planeta, en la Hipótesis de la Excéntrica, PK / KΘ tendrá aquella misma proporción.
El razonamiento, que en este caso [por ej. en la hipótesis de la excéntrica] no utilizamos esa proporción obtenida dividendo (a saber PK / KΘ) para tomar las [posiciones] estacionarias, sino más bien la proporción indivisible (a saber PΘ / KΘ), es que la velocidad del epiciclo es, en la misma proporción sobre la del planeta, (sólo) como el movimiento [medio] en longitud sobre el movimiento [medio] en anomalía, mientras la proporción de la velocidad de la excéntrica sobre la del planeta es la misma como aquella la del movimiento medio del Sol (por ej. la suma del movimiento [medio] del planeta en longitud y en anomalía) sobre el movimiento en anomalía. Por lo tanto, por ej. para Marte,
(velocidad del epiciclo / velocidad del planeta) ≈ 42 / 37
(dado que, aproximadamente, es la proporción que, como demostramos, [se] mantiene entre los movimientos [medios] en longitud y en anomalía) [5].
Por lo tanto esta también es la proporción de OΘ / ΘZ.
Pero la (velocidad de la excéntrica / velocidad del planeta) ≈ [42 + 37 =] (79 / 37),
por ej. es la misma como la proporción obtenida componendo, PΘ / ΘK,
dado que encontramos que proporción dividida, PK / KΘ, es igual a OΘ / ΘZ (por ej. 42 / 37).
Sea lo anterior suficiente para nosotros como teoremas preliminares. Resta probar que cuando uno toma las líneas [correspondientes a ZD y a BΘ] divididas en la proporción descrita, entonces en ambas hipótesis H y Θ representan los puntos en los cuales [las posiciones] estacionarias parecen tomar lugar, y [por lo tanto] el arco HGΘ debe ser retrógrado, y el resto [del círculo] poseyendo un movimiento hacia adelante. [Para este propósito,] Apolonio de Perge propone el siguiente Lema preliminar.
[Ver Fig. 12.3] En el triángulo ABG, en el que
BG > AG,
si cortamos [en GB] GD >= AG [6], entonces
GD / BD > (^ ABG / ^ BGA).
Su demostración es la siguiente.
(Él dice) completar el paralelogramo ADGE, y sean BA y GE prolongadas hasta encontrarse en Z. Entonces, dado que
AE [= GD] >= AG,
el círculo dibujado en el centro A con radio AE pasará tanto a través de G o más allá de G. Sea HEG dibujado para pasar a través de G. Luego, dado que
triángulo AEZ > sector AEH
y triángulo AEG < sector AEG,
(triángulo AEZ / triángulo AEG) > (sector AEH / sector AEG).
Pero (sector AEH / sector AEG) = (^ EAZ / ^ EAG)

y (triángulo AEZ / triángulo AEG) = (ZE / EG) (bases) [7].
En consecuencia ZE / EG > (^ ZAE / ^ EAG).
Pero ZE / EG = [ZA / AB =] GD / DB.
Y el ^ ZAE = ^ ABG
y el ^ EAG = ^ BGA.
En consecuencia GD / DB > (^ ABG / ^ AGB).
Y es obvio que si es supuesto GD (= AE), no es igual a AG, sino mayor, la diferencia en las proporciones incluso será mayor.
Ahora que hemos establecido este lema preliminar, sea ABGD [Fig. 12.4] el epiciclo con centro en E y diámetro AEG. Prolongar AEG hasta Z, [representando] nuestro punto de vista, así que
EG / GZ > (velocidad del epiciclo / velocidad del planeta) [8].
En consecuencia será posible dibujar una línea ZHB [9] de tal manera que
½ * (BH / HZ) = (velocidad del epiciclo / velocidad del planeta).
Entonces, por lo que hemos provisto previamente, si cortamos el arco AD igual al arco AB, y unimos DΘH, el punto Θ representará nuestro punto de vista en la Hipótesis de la Excéntrica, y
½ * (DH / ΘH) = (velocidad del epiciclo / velocidad del planeta).
Decimos, entonces, que en ambas hipótesis, cuando el planeta alcanza el punto H, este producirá la apariencia de estacionario, y si cortamos los arcos, no obstante muy pequeños, tanto de un lado como del otro de H, encontraremos que el arco interceptado hacia el apogeo será un arco de movimiento hacia adelante y el arco hacia el perigeo será retrógrado.
[Demostrar:] Primero, cortar arbitrariamente un arco KH hacia el apogeo, dibujar ZKL y KΘM, y unir BK y DK, y también EK y EH.
Entonces dado que, en el triángulo BKZ,
BH > BK [10],
BH / HZ > (^ HZK / ^ HBK) [cf. anterior].
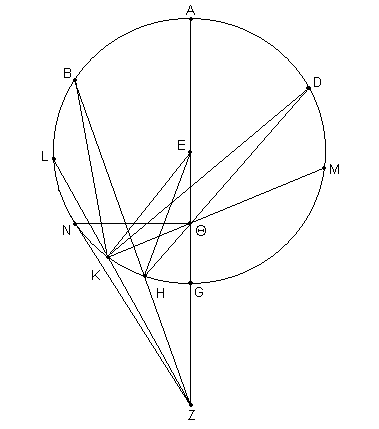
En consecuencia ½ * (BH / HZ) > (^ HZK / (2 * ^ KBH)) = (^ HZK / ^ KEH)
Pero ½ * (BH / HZ) = (velocidad del epiciclo / velocidad del planeta).
En consecuencia (^ HZK / ^ KEH) < (velocidad del epiciclo / velocidad del planeta).
Por lo tanto el ángulo que tiene la misma proporción para el ^ KEH tal como la proporción (velocidad del epiciclo / velocidad del planeta) es mayor que el ^ HZK. Sea este el ángulo ^ HZN. Entonces, en el tiempo que el planeta toma en atravesar el arco KH del epiciclo, el centro del epiciclo se ha movido en dirección opuesta por una cantidad igual a la distancia [angular] desde ZH hasta ZN. Por lo tanto esta claro que el arco KH del epiciclo ha movido el planeta hacia delante a través de un ángulo (el ^ HZK), [vértice] en nuestro ojo, que es menor que el ángulo (el ^ HZN) a través del cual [el movimiento del] epiciclo mismo lo ha movido hacia atrás durante el mismo espacio de tiempo. Por lo tanto el planeta ha experimentado un movimiento hacia delante [por la cantidad] del ^ KZN.
Similarmente, para realizar el razonamiento como si el círculo [ABGD] fuese una excéntrica [11]:
Dado que BH / HZ > (^ HZK / ^ HBK),
componendo, BZ / ZH > [^ HZK + ^ HBK =] (^ BKL / ^ HBK).
Pero BZ / ZH = DΘ / ΘH [12].
Y el ^ BKL = ^ DKM [13]
y el ^ HBK = ^ HDK.
En consecuencia DΘ / ΘH > (^ DKM / ^ HDK).
Entonces, componendo, DH / HΘ > [^ DKM + ^ HDK =] (^ HΘK / ^ HDK).
Por lo tanto, dividendo, ½ * (DH / HΘ) > ^ (HΘK / (2 * ^ HDK)) = (^ HΘK / ^ HEK).
Pero ½ * (DH / ΘH) = (velocidad de la excéntrica / velocidad del planeta).
En consecuencia (^ HΘK / ^ HEK) < (velocidad de la excéntrica / velocidad del planeta).
Por lo tanto el ángulo que mantiene la misma proporción al ^ HEK como la velocidad de la excéntrica mantiene la velocidad del planeta, es mayor que el ^ HΘK. Sea, nuevamente, el ^ HΘN. Entonces, dado que el planeta, en su movimiento propio a lo largo de KH, ha recorrido hacia adelante a través del ^ KEH, y en el mismo espacio de tiempo ha sido transportado por el movimiento de la excéntrica hacia atrás a través del ^ HΘN, que es mayor que el ^ KΘH, esta claro que, por esta [hipótesis] también, el planeta parecerá haber experimentado un movimiento hacia delante [por la cantidad] del ^ KΘN.
Es fácil de ver que, por el mismo método puede ser utilizado para probar el caso opuesto [14], si en la misma figura [Fig. 12.5] suponemos que
½ * (LK / KZ) = (velocidad del epiciclo / velocidad del planeta)
y por consiguiente ½ * (MK / ΘK) = (velocidad de la excéntrica / velocidad del planeta);
e imaginar el arco KH cortado hacia el lado del perigeo de la línea LZ.
Así que, si unimos LH para producir [(crear)] el triángulo LZH, en el que allí es cortado ZK > ZH, entonces
LK / KZ < (^ HZK / ^ HLK).
En consecuencia ½ * (LK / KZ) < (^ HZK / (2 * ^ HLK)) = (^ HZK / ^ KEH),
que es lo opuesto de lo que fue probado anteriormente [15].
Y, por el mismo razonamiento, uno llegará a una conclusión opuesta [según lo anterior, a saber] que
(^ KEH / ^ HZK) < (velocidad del planeta / velocidad del epiciclo)
y (^ KEH / ^ HΘK) < (velocidad del planeta / velocidad de la excéntrica).
Entonces, el ángulo que tiene la misma proporción [al ^ HZK o al ^ HΘK como la velocidad del planeta la tiene sobre la velocidad del epiciclo o de la excéntrica] resulta ser mayor que el ^ KEH, y el [componente del] movimiento retrógrado resultante es mayor que el de hacia adelante [(movimiento directo)].
Además, esta claro que para las distancias en las que
EG / GZ <= (velocidad del epiciclo / velocidad del planeta)
será imposible dibujar otra línea [hasta el círculo la cuál sea cortada] en una proporción igual a aquella [de las velocidades del epiciclo y del planeta], y el planeta no parecerá estacionario o retrógrado.
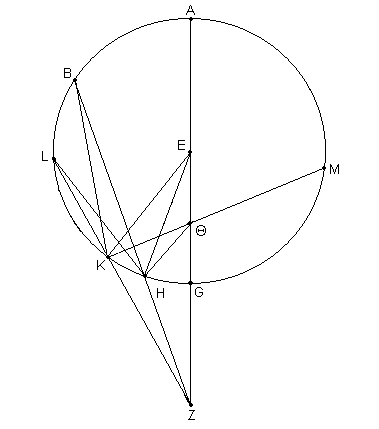
Porque dado que, en el triángulo EKZ, EG ha sido cortado y es [igual a, por ej.] no menor que EK,
(^ GZK / ^ GEK) < EG / GZ.
Pero EG / GZ <= (velocidad del epiciclo / velocidad del planeta).
En consecuencia (^ GZK / ^ GEK) < (velocidad del epiciclo / velocidad del planeta).
Por lo tanto, ya que hemos demostrado [Fig. 12.4] que, donde esto ocurre, el planeta ha experimentado un movimiento hacia adelante, [y] no encontraremos un arco, tanto sobre el epiciclo o sobre la excéntrica, sobre el cual parecerá retrógrado.
| Ir al Libro XI - Capítulo 12 | Contenidos | Capítulo Siguiente |
| Libro XII |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 |
Notas de referencia
- ↑ Sobre los capítulos del 1 al 6 [de este libro] ver HAMA 190-201, Pedersen 331-49.
- ↑ Este tipo de modelo excéntrico es de hecho aplicable también a los planetas interiores, siempre que, para la velocidad del centro de la excéntrica, uno utiliza, no la velocidad media del Sol, sino la suma de las velocidades del Sol medio con la anomalía del planeta (cuya suma es la misma como aquella del movimiento medio heliocéntrico moderno). No entiendo porque Ptolomeo no reconoce esto.
- ↑ "en esos....también" se refiere a las demostraciones más antiguas de la equivalencia de las hipótesis en el Libro III Capítulo 3 y Libro IV Capítulo 5. Notar que Ptolomeo opone su demostración () a aquellas de los primeros matemáticos, notablemente [como la] de Apolonio de Perge (, H450,9). Esto cuenta contra la suposición de Neugebauer (HAMA 264) de que Ptolomeo ha tomado de Apolonio de Perge este elegante teorema equivalente, a pesar de su relación con [su obra:] Cónicas III 37-40 y con Plane Loci II 8 ("Círculo de Apolonio").
- ↑ Dado que DZ + ZQ = 2 * OZ, y BΘ = 2 * PΘ (Euclides III 3). En consecuencia 2 * (OZ / ZQ) = 2 * (PΘ / ΘK). En consecuencia (OZ / ZΘ) = (PΘ / ΘK). Este es el último paso que es descrito como dividendo (). Ver Introducción "(i) Geométricos" para los dos sentidos de este término.
- ↑ Al principio del Libro IX Capítulo 3. 37 vueltas en anomalía corresponden alrededor de 42 vueltas en longitud y 79 años.
- ↑ Literalmente "no menor que AG".
- ↑ Euclides VI 1: los triángulos con la misma altura son proporcionales a sus bases.
- ↑ La situación donde (EG / GZ) = (velocidad del epiciclo / velocidad del planeta) es la situación límite para que el [movimiento] retrógrado ocurra: ver en este capítulo luego de la Fig. 12.4.
- ↑ Debido a Euclides III 8, que prueba que todas las líneas dibujadas hasta un círculo desde un punto fuera de él, la que atraviesa el centro, es la menor.
- ↑ Euclides III 15.
- ↑ Leer (en el manuscrito C² y en el D) en cambio de ("como sobre el círculo de la excéntrica") en H460,13.
- ↑ Esto fue probado en este capítulo [en Fig. 12.2 (DZ / ZΘ) = (BK / KΘ)].
- ↑ Euclides III 27: ángulos que subtienden arcos iguales son iguales. Por ej. Ptolomeo asume que el arco BL = arco DM. Esto se deduce del hecho que Θ es un punto fijo para un Z dado (cf. HAMA 264-5). Cf. Fig. 12.1, donde es demostrado que (AZ / ZG) = (AK / KG), por consiguiente K (aquí correspondiendo a Θ) es un punto fijo.
- ↑ Por ej. el planeta estará en [movimiento] retrógrado sobre el otro lado del punto definido por la proporción de las velocidades.
- ↑ Fig. 12.4, donde ½ * (BH / HZ) > (^ HZK / ^ KEH).
