La teoría de la relatividad de Einstein/III

III

EL SISTEMA DEL UNIVERSO SEGUN NEWTON

1. El espacio absoluto y el tiempo absoluto.

Los principios de la mecánica, tales como aquí los hemos expuesto, los encontró Newton en los trabajos de Galileo en una parte y los creó él mismo en otra parte. A él le debemos principalmente las fórmulas determinadas de las definiciones y leyes con generalidad tal, que parecen ya sin relación alguna con el experimento terrestre y pueden trasladarse a los procesos en el espacio cósmico.

Para esto hubo Newton de principiar haciendo determinadas afirmaciones sobre el espacio y el tiempo, antes de entrar propiamente en los principios mecánicos. Sin esas determinaciones, carece de sentido aun la más sencilla ley de la mecánica, la ley de inercia. Según ella, un cuerpo sobre el cual no actúa ninguna fuerza, debe moverse en linea recta uniformemente. Representémonos la mesa, sobre la cual hemos hecho experimentos con la bola. Si la bola rueda sobre la mesa en línea recta, un observador que observe su trayectoria y la mida desde otro planeta, habrá de afirmar que esa trayectoria relativamente a su punto de vista no es exactamente rectilínea. Pues la Tierra misma tiene un movimiento de rotación; y es claro que un movimiento que parece rectilíneo al observador, movido también con la Tierra, porque deja sobre la mesa un rastro en linea recta, tiene que parecer curvilíneo a otro observador que no verifique la rotación de la Tierra. Esto puede demostrarse groseramente del siguiente modo:

Un disco circular de cartón blanco es fijado a un eje, de manera que pueda hacerse girar sobre el eje por medio de una manivela; ante el disco se coloca una regla A B. Désele vueltas al disco con la mayor posible regularidad, y pásese el lápiz por junto a la regla con velocidad constante, de manera que la punta del lápiz señale su camino sobre el disco. Este camino no será, naturalmente, una recta sobre el disco, sino una curva, la cual, para mayores velocidades de rotación, puede adoptar incluso la forma de un lazo. Así, pues, el mismo movimiento, que un observador inmóvil con la regla, señala como rectilíneo y uniforme, sería considerado como circular (y no uniforme) por otro observador que estuviera en movimiento con el disco. Este movimiento puede construirse por puntos, como muestra intuitivamente el dibujo fácilmente inteligible de la figura 31.

fig31

Este ejemplo muestra claramente que la ley de inercia no tiene sentido determinado mas que si el espacio o, mejor dicho, el sistema de referencia en que debe valer la rectiliniedad está exactamente fijado.

Al sistema cósmico de Copérnico no le corresponde, naturalmente, considerar la Tierra como el sistema de referencia para el cual vale la ley de inercia, sino que éste será otro, afianzado en algún lugar del espacio cósmico. En experimentos terrestres, como el de la bola que rueda sobre la mesa, la trayectoria del cuerpo en libre movimiento no es realmente recta, sino un poco curvada. Si esto escapó y tenía que escapar a la observación primitiva, es a causa de la exigüidad de las dimensiones usadas en el experimento, en comparación con las dimensiones del globo terrestre. Aquí, como muchas veces sucede en la ciencia, contribuye la inexactitud de la observación al descubrimiento de una gran conexión; si Galileo hubiera podido hacer observaciones tan finas y exactas como los siglos posteriores, la confusión de los fenómenos hubiese dificultado grandemente el descubrimiento de la ley. Quizá no hubiese Keplero desenmarañado los movimientos planetarios, si en su tiempo se hubiesen conocido las trayectorias con la exactitud con que hoy se observan; pues las elipses de Keplero no son sino aproximaciones, de las cuales se alejan notablemente las verdaderas trayectorias, en espacios de tiempo largos. En la física actual ha sucedido cosa semejante; por ejemplo, en las regularidades del espectro; la muchedumbre del material exacto de observación ha dificultado grandemente el descubrimiento de relaciones sencillas.

Newton hubo, pues, de plantearse el problema de buscar el sistema de referencia, en que valieran la ley de inercia y los demás principios de la mecánica. Si hubiere elegido el Sol, la cuestión no hubiese quedado resuelta, sino solamente diferida; pues algún día podría descubrirse que el Sol se mueve, como es el caso efectivamente hoy.

Por estos motivos llegó Newton a la convicción de que un sistema de referencia empírico, establecido por medio de cuerpos materiales, no podía ser nunca fundamento de una ley con el contenido ideal de la ley de inercia. La ley misma parece, empero, por su estrecha relación con la teoría euclidiana del espacio, cuyo elemento es la linea recta, el punto de partida natural de la dinámica del espacio cósmico. Justamente por la la ley de inercia se manifiesta el espacio euclidiano fuera del limitado mundo terrestre. Otro tanto sucede con el tiempo, cuyo transcurso se expresa en el movimiento uniforme de la ley de inercia.

Y así llegó Newton a la concepción de que hay un espacio absoluto y un tiempo absoluto. Vamos a citar sus propias palabras. Sobre el tiempo dice:

«I. El tiempo absoluto, verdadero y matemático transcurre en sí y por su naturaleza uniformemente, y sin referencia a ningún objeto exterior. También es designado con el nombre de duración.»

«El tiempo relativo, aparente y ordinario es una medida sensible y exterior, exacta o desigual, de la duración, de la cual se usa corrientemente en lugar del verdadero tiempo; tales son hora, día, mes, año.»

«...Los días naturales, que generalmente son tenidos por iguales, como medida del tiempo, son, en realidad, desiguales. Esta desigualdad corrígenla los astrónomos midiendo el movimiento de los astros según el tiempo exacto. Es posible que no exista ningún movimiento uniforme por el cual sea posible medir el tiempo exactamente; todos los movimientos pueden ser acelerados o retrasados; sólo el transcurso del tiempo absoluto no puede ser alterado. La misma duración y la misma permanencia verificase para la existencia de todas las cosas, ya sean los movimientos veloces, lentos o nulos.»

Sobre el espacio, manifiesta Newton iguales concepciones. Dice:

«II. El espacio absoluto permanece siempre igual e inmóvil, merced a su naturaleza y sin referencia a un objeto exterior.»

«El espacio relativo es una medida o una parte móvil del primero que es caracterizada por nuestros sentidos mediante su posición respecto a otros cuerpos, y generalmente se toma por el espacio inmóvil.»

«... Así empleamos, no sin razón, en las cosas humanas, el lugar y movimientos relativos en vez del absoluto; en cambio, en la teoría de la naturaleza hay que hacer abstracción de los sentidos. En efecto, puede darse el caso de que no exista ningún cuerpo inmóvil en realidad al cual puedan referirse los lugares y movimientos.»

La expresa declaración que hace, tanto en la definición del tiempo absoluto como en la del espacio absoluto, de que éstos existen «sin referencia a un objeto exterior», parece extraña en un investigador del tipo espiritual de Newton. Este, en efecto, acentúa con gran frecuencia su propósito de no investigar sino los hechos, lo determinable por observaciones. Hypotheses non fingo; tales son sus palabras claras y contundentes. Pero algo que existe «sin relación con un objeto exterior» no es determinable, no es un hecho. Es éste, evidentemente, un caso en que representaciones de la conciencia ingenua son trasladadas sin crítica al mundo objetivo. Más tarde dedicaremos a estas cuestiones una exacta investigación.

Nuestro inmediato problema es ahora exponer cómo Newton concibió las leyes del Cosmos y en qué consiste el progreso de sus teoría.

2. Ley newtoniana de la atracción.

La idea de Newton es la concepción dinámica de las trayectorias planetarias o, como decimos hoy, la fundamentación de la mecánica celeste. Para ello era necesario aplicar a los movimientos de los astros el concepto de fuerza establecido por Galileo. Pero Newton ha descubierto la ley según la cual los astros actúan unos sobre otros, no estableciendo audaces hipótesis, sino siguiendo el camino exacto, sistemático, del análisis de los hechos conocidos sobre los movimientos planetarios. Estos hechos hallábanse expresados en las tres leyes de Keplero, que resumían todas las observaciones de aquella época por modo maravillosamente conciso e intuitivo. Vamos a dar aquí las leyes de Keplero en forma detallada.

Dicen así:

1.ª Los planetas se mueven en elipses alrededor del Sol, que ocupa uno de los focos (fig. 32).

2.ª El radio vector trazado desde el Sol a un planeta describe, en tiempos iguales, iguales superficies del espacio.

3.ª Los cubos de los ejes mayores son como los cuadrados de los tiempos de revolución.

fig32

Ahora bien; la ley fundamental de la mecánica establece una relación entre la aceleración b del movimiento y la fuerza K que ocasiona el movimiento. La aceleración b está determinada íntegramente por el curso del movimiento, y, conocido éste, puede calcularse b. Newton reconoció que la determinación de la trayectoria dada por las leyes de Keplero es bastante para calcular la aceleración; por donde resulta también conocida la fuerza activa, por la ley

$K=mb$

La matemática de la época no hubiera bastado a Newton para hacer ese cálculo; tuvo que crearse él mismo los necesarios auxilios matemáticos. Así nacieron en Inglaterra el cálculo diferencial y el cálculo integral, las raíces de toda la matemática moderna, como producto subalterno de la investigación astronómica. Al mismo tiempo, en el continente, Leibnitz (1684), partiendo de muy distintos puntos de vista, descubrió el mismo método.

Como en este libro no queremos hacer uso del cálculo infinitesimal, no podemos dar al lector una representación de la grandeza que encierran las conclusiones de Newton. Sin embargo, el pensamiento fundamental puede exponerse claramente sobre un caso sencillo.

Las trayectorias planetarias son elipses poco excéntricas, casi círculos. Será permitido admitir aproximadamente que los planetas giran alrededor del Sol describiendo círculos, como aun suponía Copérnico. Como los círculos son elipses de excentricidad igual a cero, resulta que, admitiendo eso, se cumple en todo caso la primera ley de Keplero.

Mas luego dice la segunda ley que todo planeta recorre su círculo con velocidad constante. Ahora bien; conocemos la aceleración en estos movimientos circulares, según II, 4; se dirige hacia el punto medio y, según la fórmula [3], página 39, tiene el valor

$b={\frac {v^{2}}{r}}$

siendo v la velocidad y r el radio del circulo.

Si T es el tiempo de revolución, queda determinada la velocidad como relación entre la longitud de la circunferencia 2πr (π=3,1415....) y el tiempo T. Tenemos, pues:

$v={\frac {2\pi r}{T}}$;[15]

de suerte que

$b={\frac {4\pi ^{2}r^{2}}{rT^{2}}}={\frac {4\pi ^{2}r}{T^{2}}}$

Ahora acudamos a la tercera ley de Keplero, la cual, en el caso de un círculo, dice evidentemente que la relación entre el cubo del radio, r³, y el cuadrado del tiempo de revolución, T², tiene, para todos los planetas, el mismo valor C:

${\frac {r^{3}}{T^{2}}}=C$, o sea ${\frac {r}{T^{2}}}={\frac {C}{r^{2}}}$[16]

Incluyamos esto en la fórmula anterior y tendremos:

$b={\frac {4\pi ^{2}C}{r^{2}}}$;[17]

Según esto, la cantidad de aceleración centrípeta depende solamente de la distancia que separe el planeta del Sol, y es inversamente proporcional al cuadrado de esa distancia; pero es totalmente independiente de las propiedades del planeta; verbigracia, de la masa; pues la cantidad C es la misma para todos los planetas, según la tercera ley de Keplero, y sólo tendrá algo que ver con la naturaleza del Sol, pero no con la del planeta.

Lo notable es que la misma ley, exactamente, se deriva para las trayectorias elípticas, claro que por medio de un cálculo algo más penoso. La aceleración está siempre dirigida al Sol, que se encuentra en uno de los focos y tiene la cantidad dada por la fórmula [17].

3. La gravitación universal.

La ley de la aceleración, descubierta así, tiene una importante propiedad que le es común con la gravedad terrestre: es completamente independiente de la naturaleza del cuerpo en movimiento. Si por la aceleración se calcula la fuerza, ésta es también dirigida hacia el Sol; es, pues, una atracción y tiene el valor

$K=mb=m{\frac {4\pi ^{2}C}{r^{2}}}$;[18]

es proporcional a la masa del cuerpo en movimiento, exactamente lo mismo que el peso

$G=mg$

de un cuerpo en la Tierra.

Este hecho sugiere la idea de que ambas fuerzas tienen un mismo origen. Hoy la tradición, vieja ya de varios siglos, ha dado a esa idea tal evidencia que apenas podemos representarnos la audacia y la grandeza de Newton al concebirla. ¡Cuánta fantasía no es necesaria para concebir el movimiento de los planetas alrededor del Sol, o el de la Luna alrededor de la Tierra, como una «caída» que se verifica según las mismas leyes y por la acción de la misma fuerza que la caída de una piedra que yo suelto de mi mano! Si los planetas o la Luna no van realmente a tropezar contra el cuerpo central, es porque lo impide la ley de inercia, que se manifiesta aquí como fuerza centrífuga; ya tendremos ocasión de volver a hablar de esto.

Newton comprobó primeramente sobre el ejemplo de la Luna esta ley de la pesantez o gravitación universal. La distancia de la Luna a la Tierra era conocida por mediciones de ángulos.

Esta comprobación es tan importante que vamos a insertar aquí el sencillísimo cálculo, para robustecer así el hecho de que todas las ideas físicas adquieren su validez y su valor por la concordancia de valores numéricos calculados y medidos.

El cuerpo central es ahora la Tierra. La Luna ocupa el lugar del planeta. La letra r significa el radio de la trayectoria lunar; T, el tiempo de la revolución lunar. Sea a el radio de la esfera terrestre; si la fuerza de la gravedad sobre la Tierra ha de tener el mismo origen que la atracción que la Luna experimenta por la Tierra, entonces la aceleración g de la gravedad deberá expresarse, según la ley de Newton contenida en la fórmula [17], de esta manera:

$g={\frac {4\pi ^{2}C}{a^{2}}}$,

teniendo C el mismo valor que para la Luna; a saber, según la fórmula [16]:

$C={\frac {r^{2}}{T^{2}}}$

Pónese este valor y se obtiene:

$g={\frac {4\pi ^{2}r^{2}}{T^{2}a^{2}}}$;[19]

Ahora bien; el tiempo de la revolución «sidérea» de la Luna, es decir, el tiempo que transcurre entre dos posiciones tales que la línea que une la Tierra a la Luna tenga la misma dirección hacia el cielo de las estrellas fijas, es de:

T = 27 días, 7 horas, 43 minutos y 12 segundos.
T = 2.360.592 segundos.

Es costumbre en la física no escribir más cifras que las que hayan de usarse en el cálculo posterior; las demás se expresan en potencias de 10. En este caso escribiremos:

T=2,36·10⁶

La distancia de la Luna al centro de la Tierra es unas 60 veces el radio terrestre; más exactamente,

r = 60,1 a.

El radio terrestre es fácil de obtener, puesto que el sistema métrico está en una relación sencilla con él. Es, en efecto, 1m. = 100 cm. la diezmillonésima parte del cuadrante de la Tierra; es decir, la 40 millonésima, o cuatro veces la 10⁷esima parte de la circunferencia terrestre 2πa:

$100={\frac {2\pi a}{4\cdot 10^{7}}}$

o sea:

$a=6,36\cdot 10^{8}$ cm.[20]

Incluyese todo esto en la fórmula [12] y se obtiene:

$g={\frac {2\pi ^{2}\cdot 60,1^{2}\cdot 6,37\cdot 10^{8}}{2,36^{2}\cdot 10^{1}2}}=981{\text{cm.}}/{\text{sec.}}^{2}$.[21]

Este valor, empero, coincide exactamente con el que se obtiene por medio de observaciones del péndulo en la Tierra.

La gran importancia de este resultado es que significa la relativización de la gravedad. Para los antiguos significaba el peso un tiro hacia el «abajo» absoluto, que experimentan todos los cuerpos terrestres. El descubrimiento de la forma esférica de la Tierra trajo consigo la relativización de la dirección de la gravedad terrestre; fué concebida como un tiro o atracción hacia el centro de la Tierra.

Ahora ha quedado demostrada la identidad entre la pesantez y la fuerza de atracción que obliga a la Luna a girar, y como no cabe duda alguna de que ésta es esencialmente igual a la fuerza que obliga a la Tierra y a los demás planetas a recorrer su trayectoria en torno al Sol, surge de aquí la representación de que los cuerpos no son pesados en absoluto, sino relativamente unos a otros. La Tierra, como planeta, es atraída hacia el Sol; pero, a su vez, atrae a la Luna. Evidentemente es ésta una descripción aproximada del verdadero estado de cosas, que consiste en que el Sol, la Tierra y la Luna se atraen recíprocamente. Desde luego, para la trayectoria de la Tierra en torno al Sol, éste puede considerarse con gran aproximación como inmóvil, porque su enorme masa impide que se produzcan notables aceleraciones, y, recíprocamente, la Luna, por su pequeñez, no entra notablemente en consideración. Pero una teoría exacta tendrá que tomar en cuenta estas influencias, llamadas «perturbaciones».

Antes de considerar más de cerca esta concepción, que significa el progreso principal de la teoría newtoniana, vamos a dar su forma definitiva a la ley de Newton. Hemos visto que un planeta que se encuentra a la distancia r del Sol sufre una fuerza de atracción hacia el Sol de cantidad determinada por la fórmula [18]:

$K=m{\frac {2\pi ^{2}C}{r^{2}}}$,

siendo C una constante que depende de las propiedades del Sol, no del planeta. Según la nueva concepción de la atracción recíproca, tiene el planeta que atraer igualmente al Sol; si M es la masa del Sol, c una constante que sólo depende de la naturaleza del planeta, tendrá la fuerza de atracción del planeta sobre el Sol la expresión

$K'=M{\frac {2\pi ^{2}c}{r^{2}}}$,

Ahora bien; anteriormente, cuando introdujimos el concepto de fuerza, hubimos de hacer uso del principio de la acción reciproca (acción = reacción), que es una de las leyes más sencillas y seguras de la mecánica. Apliquémoslo ahora. Tendremos que poner $K=K'$, o sea:

$m{\frac {2\pi ^{2}C}{r^{2}}}=M{\frac {2\pi ^{2}c}{r^{2}}}$;

de donde se sigue:

$mC=Mc$;

o sea:

${\frac {C}{M}}={\frac {c}{m}};$

esto es, que esta relación tiene para ambos cuerpos—Sol y planeta—, y por tanto para todos los cuerpos en general, el mismo valor. Designemos este valor con ${\tfrac {k}{4\pi ^{2}}}$ y podremos escribir:

$4\pi ^{2}C=kM,\qquad 4\pi ^{2}c=km$.[22]

El factor de proporcionalidad k llámase constante de gravitación.

Entonces la ley newtoniana de la gravitación universal recibe la forma simétrica siguiente:

$K=k{\frac {mM}{r^{2}}};$[23]

o, dicha en palabras:

Dos cuerpos se atraen uno a otro con una fuerza que es directamente proporcional a la masa de cada uno de los cuerpos e inversamente proporcional al cuadrado de su distancia.

4. La mecánica del cielo.

Sólo en esta acepción general representa la ley de Newton un progreso real para el cálculo de las trayectorias planetarias. Pues en la primitiva forma fué derivada por cálculo de las leyes de Keplero, y no significaba mas que un brevísimo y exacto compendio de esas leyes. Puede demostrarse recíprocamente que el movimiento de un cuerpo alrededor de otro cuerpo central inmóvil que le atrae, según la ley de Newton, es necesariamente un movimiento elíptico kepleriano. Pero algo nuevo surge si primero consideramos ambos cuerpos como en movimiento y luego añadimos otros cuerpos más.

Nace entonces el problema matemático de los tres o más cuerpos, que corresponde exactamente a las relaciones efectivas en el sistema planetario (fig. 33). En efecto; los planetas no son atraídos solamente por el Sol, ni la Luna solamente por su planeta, sino que todo cuerpo, ya sea sol, planeta, satélite, cometa, atrae a los demás. Entonces aparecen las leyes de Keplero como valederas sólo aproximativamente, porque la atracción del Sol, dada la gran masa de éste, supera con mucho la acción recíproca de todos los demás cuerpos del sistema planetario. Pero en largos periodos de tiempo han de poderse notar esas acciones recíprocas como desviaciones de las leyes de Keplero; hablaré, pues, como ya hemos dicho, de anomalías o perturbaciones.

fig33

Ya en la época de Newton eran conocidas tales anomalías, y los siglos posteriores han amontonado un enorme material de hechos, merced al refinamiento en los métodos de observación. La teoría newtoniana de la atracción tenía que dominarlo y explicarlo. Lo ha conseguido, y es éste uno de los más grandes triunfos del espíritu humano.

No es nuestro objeto aquí exponer la evolución de la mecánica celeste desde Newton hasta nuestros días, ni explicar los métodos matemáticos que se han inventado para calcular las trayectorias «anómalas». Los más sutiles matemáticos de todos los países han colaborado en la teoría de las anomalías, y si el problema de los tres cuerpos no ha encontrado todavía una solución perfectamente satisfactoria, se puede, sin embargo, calcular con seguridad los movimientos a cientos de miles o millones de años en el futuro o en el pasado. Innumerables casos han comprobado, pues, la teoría de Newton por nuevas experiencias, y hasta ahora nunca ha fallado— salvo en un caso de que ahora nos vamos a ocupar—. La astronomía teórica, tal como Newton la había fundado, pasaba, pues, como modelo de las ciencias exactas. Realiza la que ha sido siempre aspiración del hombre: descorrer el velo que se tiende sobre el futuro, dando a sus discípulos el don de la profecía. Y si el objeto de las predicciones astronómicas es poco importante, indiferente para la vida humana, tornóse, empero, en un símbolo de la liberación del espíritu que rompe las barreras de la limitación terrestre; también nosotros, como los pueblos de todos los tiempos, miramos a los astros con admiración respetuosa, porque ellos nos descubren la ley del universo.

fig34

Pero la ley del universo no admite excepción. Y, sin embargo, hay un caso, ya lo hemos indicado, en que la teoría de Newton ha fallado. Aun cuando el error es pequeño, no vale negarlo. Trátase del planeta Mercurio, el mas próximo de todos al Sol. La trayectoria de todo planeta puede concebirse como un movimiento elíptico kepleriano, que es perturbado por los demás planetas; es decir: la posición del plano de la trayectoria, la situación del eje máximo de la elipse, su excentricidad, en suma, los elementos de la trayectoria experimentan poco a poco variaciones. Cuando se calculan éstas según la ley de Newton y se incluyen en la trayectoria observada, tiene ésta que transformarse en un movimiento kepleriano exacto, en una elipse situada en determinado plano, con un eje máximo de determinada dirección y longitud, etc. Tal es el caso, efectivamente, en todos los planetas; pero en Mercurio queda un pequeño residuo. La dirección del eje máximo, esto es, la linea que une el Sol con el mas próximo punto de la trayectoria, el perihelio (fig. 34), no queda fijo después de computadas todas las perturbaciones, sino que verifica un lentísimo movimiento de rotación, progresando 43 segundos de arco en un siglo. El astrónomo Leverrier (1845)—el mismo que predijo la existencia del planeta Neptuno, fundándose en cálculos de anomalías o perturbaciones—fué el primero que calculó ese movimiento, que está establecido con gran seguridad. Pues bien; resulta inexplicable por la atracción newtoniana de las masas planetarias que conocemos. Se ha acudido al recurso de admitir masas hipotéticas, cuya atracción habría de producir el movimiento del perihelio de Mercurio; así, por ejemplo, se puso en relación con la anomalía de Mercurio la luz del zodíaco, que procedería de una materia poco densa, a manera de nube en torno al Sol. Esta y otras muchas hipótesis tienen todas un defecto, y es el de estar inventadas expresamente para el caso, sin que las compruebe ninguna otra observación.

El hecho de que la única desviación de las leyes de Newton que haya sido establecida con certeza se refiera precisamente a Mercurio, el planeta más próximo al Sol, parece indicar que puede haber aquí un defecto de principio en la ley de Newton. Pues la fuerza de atracción es máxima en las inmediaciones del Sol y, por lo tanto, aquí es donde serán más notables cualesquiera desviaciones de la ley del cuadrado inverso de la distancia. Se ha intentado introducir modificaciones en la ley de Newton; pero, por ser inventadas caprichosamente, sin que pueda comprobarlo ningún otro hecho, no puede su exactitud demostrarse por sólo que expongan y traduzcan el movimiento del perihelio de Mercurio. Si la teoría de Newton exige realmente un perfeccionamiento, hay que desear que, sin la introducción de constantes caprichosas, se derive de un principio que supere a la teoría en generalidad y verosimilitud interna.

Einstein es quien lo ha conseguido, poniendo a la base de las leyes naturales la relatividad general como postulado supremo. En el último capitulo volveremos sobre su explicación del movimiento del perihelio de Mercurio.

5. El principio de relatividad de la mecánica clásica.

Sumidos en los grandes problemas del Cosmos, casi hemos olvidado su punto de partida terrestre. Las leyes de la dinámica, encontradas sobre la Tierra, han sido trasladadas al espacio cósmico que la Tierra surca con poderosa velocidad en su trayectoria alrededor del Sol. ¿Cómo es que nosotros advertimos tan poca cosa de ese viaje por el espacio? ¿Cómo es que Galileo pudo encontrar, sobre la Tierra en movimiento, leyes que, según Newton, sólo podían valer estrictamente en el espacio absolutamente inmóvil? Ya hemos aludido antes a este problema, cuando tratamos de las concepciones newtonianas del espacio y del tiempo. Dijimos entonces que la trayectoria de una bola que rueda sobre una mesa es, al parecer, recta; pero que, en realidad, a causa de la rotación de la Tierra, tiene que ser algo curva, pues no es recta con relación a la Tierra que gira, sino con relación al espacio absoluto; si no se advierte esa curvatura, es por la brevedad del camino y del tiempo de observación, durante el cual la Tierra ha girado muy poco sobre sí. Convengamos en esto; pero aun queda el movimiento alrededor del Sol, que se verifica con la enorme velocidad de unos 30 kilómetros por segundo. ¿Por qué no advertimos nada de éste?

Este movimiento alrededor del Sol es, sin duda, una rotación también, y tiene que observarse en los movimientos terrestres, del mismo modo que la rotación de la Tierra sobre su eje, aunque más débilmente, porque la curvatura de la trayectoria de la Tierra es pequeñísima. Pero nuestra pregunta se refiere, no a ese movimiento de rotación, sino al movimiento de traslación, que, en el curso de un día, es prácticamente rectilíneo y uniforme.

De hecho verifícanse todos los procesos mecánicos sobre la Tierra como si ese poderoso movimiento de avance no existiera; y esta ley tiene una validez general para todo sistema de cuerpos, que realiza un movimiento uniforme y rectilíneo por el espacio absoluto de Newton. Este se llama principio de relatividad de la mecánica clásica; puede formularse de diferentes modos; provisionalmente damos el siguiente:

Las leyes de la mecánica formúlanse igualmente, ya sean referidas a un sistema de coordenadas en movimiento rectilíneo y uniforme por el espacio absoluto, ya sean referidas a un sistema de coordenadas inmóvil en el espacio absoluto.

Para comprender la exactitud de este principio, basta fijar la atención en la ley fundamental de la mecánica, la ley de la impulsión, y en los conceptos que contiene. Sabemos que un choque produce una variación de velocidad; pero esta variación es en absoluto independiente de que las velocidades antes y después del choque, v₁ y v₂, sean juzgadas con referencia al espacio absoluto o a un sistema de referencia que se mueva con la velocidad constante a. Si el cuerpo en movimiento va por el espacio con la velocidad v₁ = 5 cm./sec, antes del choque o impulso, un observador que se mueva en la misma dirección con la velocidad a = 2 cm./sec, no medirá más que la velocidad relativa

$v_{1}=v_{1}-a=5-2=3$.

Si ahora el cuerpo recibe, en la dirección del movimiento, un choque o impulso que aumenta su velocidad a v₂=7 cm./sec, entonces el observador en movimiento medirá la velocidad final de

$v_{2}=v_{2}-a=7-2=5$.

La variación de velocidad producida por el choque es, pues, en el espacio inmóvil:

$w=v_{2}-v_{1}=v_{1}=7-5=2$.

En cambio, el observador en movimiento determina el siguiente aumento de velocidad:

$w'=v'_{2}-v'_{1}=(v_{2}-a)-(v_{1}-a)=v_{2}-v_{1}=w=5-3=2$.

Ambos son iguales.

Lo mismo ocurre en las fuerzas continuas y en las aceleraciones que ellas producen. Pues la aceleración b quedó definida como relación entre la variación de velocidad, w y el tiempo necesario para ello, t; y como w es independiente del movimiento traslativo rectilíneo y uniforme que tenga el sistema de referencia usado para la medición, resulta que lo mismo vale para b.

El fundamento de esta ley es, sin duda alguna, la ley de inercia, según la cual un movimiento de traslación se verifica sin fuerzas; un sistema de cuerpos moviéndose todos por el espacio con la misma velocidad constante, no sólo está en quietud relativa geométricamente, sino que no se produce, a consecuencia del movimiento, ningún efecto de fuerzas en los cuerpos del sistema. Pero si los cuerpos del sistema ejercen fuerzas unos sobre otros, los movimientos así producidos se verificarán relativamente, tal como si no existiera el movimiento de traslación común. El sistema, pues, para un observador que vaya arrastrado en su movimiento, no es discernible de un sistema que se hallare en quietud absoluta.

La experiencia diaria, mil veces repetida, de que no advertimos nada del movimiento de traslación de la Tierra, es una palpable demostración de esta ley. Mas lo mismo sucede en movimientos que se verifican en la Tierra; pues cuando un movimiento sobre la Tierra es rectilíneo y uniforme relativamente a ésta, lo es también relativamente al espacio, si en el movimiento de la Tierra prescindimos de la rotación. Todo el mundo sabe que en un barco o en un vagón de ferrocarril, cuando se mueve uniformemente, los procesos mecánicos suceden de la misma manera que en la Tierra inmóvil; sobre el barco que se mueve cae, por ejemplo, una piedra verticalmente, esto es, a lo largo de una recta vertical que se mueve con el barco. Si la navegación fuese perfectamente uniforme y sin sacudidas, los pasajeros nada notarían del movimiento, mientras no observasen nada de lo que rodea al barco.

6. El espacio absoluto «limitadamente».

El principio de la relatividad de los procesos mecánicos es el punto de partida para todas nuestras consideraciones ulteriores. Su importancia obedece a que está en estrechísima conexión con las concepciones de Newton sobre el espacio absoluto, y a que desde un principio limita esencialmente la realidad física de ese concepto.

Hemos fundado antes la necesidad de admitir el espacio absoluto y el tiempo absoluto, en la consideración de que, sin ello, la ley de inercia carece de sentido. Ahora ya debemos meditar la cuestión de hasta qué punto conviene a esos conceptos la nota de «realidad» en el sentido de la física. Un concepto tiene realidad física sólo cuando en el mundo de los fenómenos le corresponde algo determinable por medio de mediciones. No es ésta ocasión de describir el concepto filosófico de realidad. En todo caso, es lo cierto que el criterio de realidad que acabamos de indicar corresponde exactamente al caso de las ciencias físicas; un concepto que no le satisfaga, queda poco a poco excluído del sistema de la física.

Vemos inmediatamente que, en tal sentido, un determinado lugar en el espacio absoluto de Newton no es nada real; pues es, en principio, imposible encontrar de nuevo en el espacio un lugar.

Ello se infiere sin dificultad del principio de relatividad. Suponiendo que hubiésemos llegado por algún método a admitir que en el espacio descansa un determinado sistema de referencia, siempre podrá considerarse con el mismo derecho, como inmóvil, un sistema de referencia que, relativamente al primero, se mueva con movimiento uniforme y rectilíneo. Los procesos mecánicos en ambos se verifican con perfecta igualdad, y ninguno de los sistemas es privilegiado con respecto al otro. Un determinado cuerpo, que aparece inmóvil en uno de los dos sistemas de referencia, describe, visto desde el otro, un movimiento rectilíneo uniforme; y si alguien quisiera sostener que el tal cuerpo señala un lugar en el espacio absoluto, otra persona podría negarlo, con igual derecho, y decir que el cuerpo está en movimiento.

Pero con esto el espacio absoluto de Newton pierde ya una parte importante de su existencia algo desazonadora; un espacio en donde no hay lugar alguno que pueda determinarse por medios físicos es, en todo caso, algo bien sutil, y no ya sólo un cajón en donde se amontonan las cosas materiales.

Debemos, pues, ahora variar un poco la fórmula del principio de relatividad, porque en ella se habla de un sistema de coordenadas inmóvil en el espacio absoluto, lo que evidentemente carece de sentido físico. Para llegar a una expresión clara, hase introducido el concepto de sistema inercial, por el cual entiéndese un sistema de coordenadas en donde se verifica la ley de inercia en su acepción primitiva; no hay un solo sistema de referencia inmóvil en el espacio absoluto de Newton, sino infinitos, en que eso sucede, y todos son igualmente legítimos; mas como no se puede hablar de «muchos» espacios en movimiento unos con respecto de otros, prefiérese, en lo posible, evitar la palabra espacio. Entonces el principio de relatividad recibe la siguiente forma:

Hay infinitos sistemas en movimiento de traslación unos relativamente a otros, y todos igualmente legítimos; en esos sistemas inerciales son válidas las leyes de la mecánica en su forma sencilla, clásica.

Se ve claramente cómo el problema del espacio está en estrechísima relación con la mecánica. No es el espacio el que existe e imprime su «forma» a las cosas, sino las cosas y sus leyes físicas son las que determinan el espacio. Luego veremos cómo esta concepción va imponiéndose con creciente claridad y amplitud, hasta alcanzar su máximo valor en la teoría general de la relatividad de Einstein.

7. Transformaciones de Galileo.

Aun cuando todas las leyes de la mecánica son las mismas en todos los sistemas inerciales, no por eso se sigue que las coordenadas y las velocidades de los cuerpos con respecto a dos sistemas inerciales en movimiento uno relativamente al otro, sean las mismas. Pues si, por ejemplo, un cuerpo está inmóvil en un sistema S, tendrá una velocidad constante con respecto al otro sistema S', que se mueve relativamente a S. Las leyes generales de la mecánica no contienen mas que las aceleraciones, y éstas son, como hemos visto, iguales para todos los sistemas inerciales; pero para las coordenadas y las velocidades no es lo mismo.

De aquí se origina el problema siguiente: dadas la posición y la velocidad de un cuerpo en un sistema inercial S, hallarlas para otro sistema inercial S'.

fig35

Trátase, pues, del tránsito de un sistema de coordenadas a otro que se mueve con relación al primero. Debemos hacer aquí algunas observaciones en general sobre los sistemas de coordenadas igualmente legítimos y sobre las leyes del cálculo para pasar de uno a otro, las llamadas ecuaciones de transformación.

fig36

El sistema de coordenadas es, en geometría, un medio de fijar cómodamente las posiciones relativas de un cuerpo con respecto a otro. Para lograrlo se imagina el sistema de coordenadas fijo en uno de los cuerpos, y entonces las coordenadas de los puntos del otro cuerpo determinan íntegramente la posición relativa. Naturalmente, es indiferente que el sistema de coordenadas sea rectangular o de ángulo agudo, polar o más general aún; también es indiferente la orientación con respecto al primer cuerpo. Ahora bien; o hay que determinar esa orientación, o, si ésta cambia, hay que indicar exactamente cómo el sistema de coordenadas forma campo con respecto al cuerpo. Si, por ejemplo, se opera en el plano con coordenadas rectangulares, puede elegirse, en lugar del sistema S primeramente elegido, un segundo sistema S' que esté detrás del primero (figura 35), o que sea resultado de un giro en torno al primero (figura 36); pero habrá que decir exactamente la cantidad que vale la distancia o el giro que separan a ambos. Dados estos datos, puede calcularse luego qué valor tendrán, en el nuevo sistema S', las coordenadas de un punto P, que en el viejo sistema S tenían los valores x é y. Si llamamos a esos valores x' é y', se obtienen fórmulas que permiten calcular x' é y' por medio de x é y. Vamos a desarrollar esto para el caso más sencillo, a saber: cuando S' se origina de S corriendo el eje de las y paralelamente sobre el eje de las x a una distancia del punto cero igual a a (fig. 37). En este caso, la nueva coordenada x' de un punto P es igual a su anterior coordenada x disminuida de la distancia a; en cambio, la coordenada y es la misma en los dos sistemas. Tenemos, pues:

fig37

$x'=x-a,\quad y'=y$.[24]

Semejantes, si bien más complicadas, fórmulas de transformación valen para otros casos. Más tarde habremos de hablar detenidamente de ellas. Importante es conocer que toda magnitud que tiene en sí una significación geométrica debe ser independiente de la elección del sistema de coordenadas y, por lo tanto, expresarse homogéneamente en sistemas de coordenadas homogéneos.

Se dice que tal magnitud es invariante con respecto a la referida transformación de coordenadas. Tomemos, por ejemplo, la transformación explicada más arriba en la fórmula [24], que expresa un desplazamiento paralelo del eje de las y a lo largo del de las x; es evidente que la diferencia de las coordenadas x de dos puntos P y Q, x₂—x₁ no varia; en realidad, es (fig. 38):

$x'_{2}-x'_{1}=(x_{2}-a)-(x_{1}-a)=x_{2}-x_{1}.$

En el caso más general de que el sistema de coordenadas se desplace, y también gire, será invariante la distancia entre dos puntos P y Q. Las invariantes son especialmente importantes, porque expresan relaciones geométricas en sí mismas, sin referencia a la elección contingente del sistema de coordenadas. En lo que sigue habrán de tener un papel importante.

fig38

Dejemos esta digresión geométrica y volvamos al punto de partida. Hemos de contestar la pregunta: ¿cuáles son las leyes de transformación para el tránsito de un sistema inercial a otro?

Hemos definido el sistema inercial como un sistema de coordenadas en que rige la ley de inercia. Lo esencial aquí es el estado de movimiento, a saber: la ausencia de aceleraciones respecto del espacio absoluto. En cambio, la especie y posición del sistema de coordenadas es inesencial. Si se elige éste, como generalmente se hace, rectangular, sigue siendo libre su posición; puede tomarse un sistema retraído o detenido en un proceso giratorio, como se quiera, con tal de que tenga el mismo estado de movimiento. En las páginas precedentes hemos empleado la expresión de sistema de referencia, cuando lo importante era el estado de movimiento y no la especie y posición del sistema de coordenadas; de aquí en adelante usaremos sistemáticamente esa expresión.

Si el sistema inercial S' se mueve en línea recta con respecto a S con la velocidad v, podemos elegir en ambos sistemas de referencia coordenadas rectangulares; de tal suerte que la dirección del movimiento sea el eje de las x y, respectivamente, de las x'. Podemos admitir, además, que en el tiempo t=0 coinciden los puntos-cero de ambos sistemas. Luego el punto-cero del sistema S' ha corrido en el tiempo t una distancia a = vt en la dirección x; en este momento, los dos sistemas tienen, pues, la misma situación exactamente que fué estudiada antes desde un punto de vista puramente geométrico; valen, pues, las ecuaciones de la fórmula [24], en las que hay que poner a=vt. Obtiénense, pues, las ecuaciones de transformación siguientes:

$x'=x-vt,\quad y'=y,\quad z'=z,$[25]

fórmula en que hemos incluido la coordenada z invariable. Llámase a esta ley transformación de Galileo, en honor del fundador de la mecánica.

Ahora puede el principio de la relatividad expresarse como sigue:

Las leyes de la mecánica son invariantes respecto de las transformaciones de Galileo.

Esto proviene de que las aceleraciones son invariantes, como ya hemos visto antes, al considerar la variación de velocidad de un cuerpo relativamente a dos sistemas inerciales.

Ya hemos explicado que la teoría del movimiento, o cinemática, puede considerarse como una geometría en el espacio de cuatro dimensiones x,y, z, t, en el universo de Minkowski. Por eso no carece de interés el meditar lo que significan en esta geometría cuatridimensional los sistemas inerciales y las transformaciones de Galileo. Esto no es difícil, pues las coordenadas y y z no entran en la transformación; basta, pues, operar en el plano xt.

Representemos un sistema inercial S por un sistema rectangular de coordenadas xt (fig 39). A un segundo sistema inercial S' corresponde entonces otro sistema de coordenadas x't', y se trata de saber cómo es éste y cómo está situado con respecto al primero. Ante todo, la medida del tiempo del segundo sistema S' es exactamente la misma que en el primero, a saber: el tiempo uno, absoluto, t =t'; así, pues, el eje x, en el cual t = 0, coincide con el eje x', en que t' = 0. Por consiguiente, el sistema S' no puede ser sino un sistema de coordenadas en ángulo agudo. El eje t' es la línea universal del punto x'=0, esto es, del punto 0 del sistema S'; la coordenada x de este punto, que se mueve con la velocidad v, relativamente al sistema S, es en este sistema, en el tiempo t, igual a vt. Para un punto universal cualquiera P, da la figura la fórmula de la transformación de Galileo

$x'=x-vt$.

fig39

A cualquier sistema inercial le corresponde otro sistema acutangular de coordenadas xt, con el mismo eje x, pero un eje t inclinado diferentemente. El sistema rectangular de que partimos no tiene, entre todos esos sistemas acutangulares, ninguna preferente posición. La unidad de tiempo es cortada en todos los ejes t de los diferentes sistemas de coordenadas por la misma paralela al eje x; es en cierto modo la «curva tipo» del plano xt con respecto al tiempo.

Resumen del resultado:

En el plano xt, la elección de la dirección del eje t es totalmente contingente. En todo sistema acutangular de coordenadas xt, con el mismo eje x, rigen las leyes fundamentales de la mecánica.

Desde un punto de vista geométrico, esa multiplicidad de sistemas de coordenadas, igualmente válidos, es muy extraña y desacostumbrada; particularmente es notable la posición firme o invariancia del eje x. Cuando en geometría se opera con coordenadas acutangulares, no hay generalmente fundamento alguno para mantener fija la posición de un eje. Pero esto físicamente es exigido por el principio newtoniano del tiempo absoluto. Todos los sucesos que se verifican simultáneamente, con el mismo valor de t, quedan representados por una paralela al eje x; puesto que, según Newton, el tiempo corre en absoluto y sin referencia a ningunos objetos, habrán de corresponder en todos los sistemas de coordenadas admisibles los mismos puntos universales a los sucesos simultáneos.

Ya veremos que esta asimetría en el comportamiento de las coordenadas universales 'x y t, que aquí sólo calificamos de defecto de belleza, no existe en realidad. Einstein la ha reducido, por medio de su relativización, del concepto de tiempo.

8. Fuerzas de inercia.

Después que ya hemos conocido que a los lugares, en el espacio absoluto de Newton, no les corresponde en ningún caso realidad física alguna, habremos de preguntar qué es lo que resta, en general, de ese concepto. Ahora bien; el tal concepto se hace notable con fuerza y claridad, porque la resistencia de todos los cuerpos a las aceleraciones debe, en el sentido de Newton, interpretarse como un efecto del espacio absoluto. La locomotora que pone el tren en movimiento ha de vencer la resistencia de inercia; el cañonazo que arruina una pared toma de la inercia su fuerza destructiva. Surgen efectos de inercia dondequiera que se verifican aceleraciones, y éstas no son sino variaciones de velocidad en el espacio absoluto; puede emplearse aquí esta palabra, pues una variación de velocidad tiene el mismo valor en todos los sistemas inerciales. Los sistemas de referencia, que son acelerados respecto de los sistemas inerciales, no son, pues, de igual valor que éstos, ni tampoco entre sí; es posible, sin duda, referir a ellos las leyes de la mecánica; pero éstas adoptan entonces una nueva forma, más complicada. La trayectoria de un cuerpo abandonado a sí mismo no es, en un sistema acelerado, rectilínea y uniforme (véase III, 1, pág. 67); esto puede también expresarse así: en un sistema acelerado actúan, además de las fuerzas propiamente tales, otras fuerzas aparentes: las fuerzas de inercia; un cuerpo sobre el cual no actúa ninguna fuerza real está sometido, sin embargo, a esas fuerzas de inercia, y su movimiento, por tanto, no es, en general, ni uniforme ni rectilíneo. Sistema acelerado es, por ejemplo, un vagón al arrancar o al frenar; todo el mundo conoce la sacudida que el tren da al arrancar y al detenerse; ésta no es otra cosa que la fuerza de inercia de que acabamos de hablar.

Vamos a considerar los fenómenos en particular para un sistema S, movido en línea recta y cuya aceleración es constantemente igual a k. Si medimos la aceleración b de un cuerpo con respecto a ese sistema en movimiento S, resultará que la aceleración respecto del espacio absoluto es, evidentemente, mayor, y éste exceso tiene el valor de k. Por eso dice la ley dinámica fundamental, referida al espacio:

$m(b+k)=K$.

Si se escribe ahora en la forma:

$mb=K-mk$,

podrá decirse que en el sistema acelerado S rige, a su vez, una ley de movimiento con la forma newtoniana

$mb=K'$

habiendo de ponerse para K' la suma

$K'=K-mk$,

siendo K la fuerza real y —mk la fuerza aparente o de inercia.

Ahora bien; si no hay ninguna fuerza real; si, pues, K=0, la fuerza total es igual a la fuerza de inercia,

$K'=-mk$.[26]

Esta actúa, pues, en un cuerpo abandonado a sí mismo. Puede conocerse su efecto por la reflexión siguiente: ya sabemos que la gravedad terrestre, el peso» está determinada por la fórmula G=mg, siendo g la constante aceleración de la gravedad. La fuerza de inercia K' = -mk actúa, pues, lo mismo que la gravedad. El signo menos significa que la fuerza es de dirección opuesta a la aceleración del sistema de referencia S que nos sirve de base; la cantidad de la aparente aceleración de la gravedad k es igual a la aceleración del sistema de referencia S. Así, pues, el movimiento de un cuerpo abandonado a sí mismo en el sistema S es, simplemente, un movimiento de caída o de proyección.

Esta conexión entre las fuerzas de inercia en los sistemas acelerados y la gravedad aparece aquí enteramente contingente; en realidad, han pasado dos siglos sin que nadie la advierta. Pero desde ahora queremos decir que constituye el fundamento de la teoría de la relatividad de Einstein.

9. Las fuerzas centrífugas y el espacio absoluto.

En la concepción de Newton, la aparición de las fuerzas de inercia en sistemas acelerados demuestra la existencia del espacio absoluto, o mejor dicho la posición privilegiada de los sistemas inerciales. Las fuerzas de inercia manifiéstanse con especial claridad en los sistemas giratorios de referencia, bajo la forma de fuerzas centrífugas. En éstas apoyaba Newton principalmente su teoría del espacio absoluto. Citaremos sus propias palabras:

«Las causas eficientes, por las cuales son diferentes uno de otro el movimiento absoluto y el relativo, son las fuerzas centrífugas que se apartan del eje del movimiento. En un movimiento circular meramente relativo no existen esas fuerzas; pero son más pequeñas o mayores según la relación de la magnitud del movimiento (absoluto).»

«Cuélguese, por ejemplo, un vaso de una cuerda muy larga y désele vueltas constantemente, hasta que la cuerda se ponga muy rígida por la rotación (fig. 40); llénese luego de agua y manténgase la cuerda inmóvil. Si de pronto una fuerza activa produce un movimiento giratorio en sentido opuesto y éste dura bastante tiempo, mientras que la cuerda se deslía, la superficie del agua es al principio plana, como antes del movimiento del vaso; y luego, cuando la fuerza poco a poco actúa sobre el agua, el vaso es causa de que ésta empiece a girar notablemente. Aléjase poco a poco del centro, y sube por las paredes del vaso hacia lo alto, en donde adopta una forma hueca. (Este experimento lo he hecho yo mismo.)»

fig40

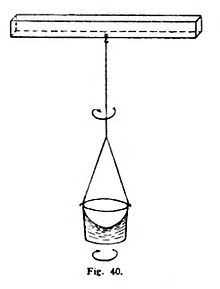
«... Al principio, cuando el movimiento relativo del agua en el vaso (respecto de las paredes) era máximo, no ocasionaba ninguna tendencia a alejarse del eje. El agua no intentaba acercarse a la extensión, subiendo por las paredes, sino que permanecía plana, y el verdadero movimiento circular no había comenzado todavía. Pero luego, cuando disminuyó el movimiento relativo del agua, empezó a subir por las paredes del vaso, manifestando así su tendencia a alejarse del eje, y esta tendencia la mostró el verdadero movimiento circular, siempre creciente, del agua; hasta que llega este movimiento a ser máximo, cuando el agua misma estaba relativamente inmóvil en el vaso.»

«... Conocer los verdaderos movimientos de los cuerpos particulares y distinguirlos de los aparentes es, por lo demás, cosa muy difícil, porque las partes de ese espacio inmóvil en que los cuerpos se mueven verdaderamente no pueden ser conocidas por los sentidos.»

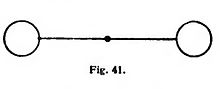
«... Pero la cosa no es enteramente desesperada. Ofrécense, en efecto, los medios necesarios, en parte por los movimientos aparentes, que son la distinciones de los verdaderos, y en parte también por las fuerzas que como causas eficientes sirven de fundamento a los movimientos verdaderos. Si dos bolas, por ejemplo, a distancia dada una de otra, se unen por un hilo y se les da vueltas alrededor del punto de gravedad (fig. 41), se reconoce por la tensión del hilo la tendencia de las bolas a alejarse del eje del movimiento, y por esto puede conocerse la cantidad del movimiento circular. De esa manera podría hallarse no sólo la cantidad, sino también la dirección de ese movimiento circular en cualquier espacio vacío infinitamente grande, aunque no se encontrase en él nada exterior y cognoscible con que las bolas pudieran compararse.»

fig41

Estas palabras indican el sentido clarísimo del espacio absoluto; pocas explicaciones añadiremos nosotros.

Primeramente, en lo que se refiere a las relaciones cuantitativas de las fuerzas centrífugas, podemos comprenderlas en seguida recordando la cantidad y dirección de la aceleración en movimientos circulares; estaba dirigida hacia el centro, y, según la fórmula [3] (pág. 39), valía:

$b={\frac {v^{2}}{r}}$

siendo r el radio y v la velocidad.

Si tenemos un sistema de referencia giratorio S, que en T segundos da una vuelta, resultará que la velocidad de un punto situado a la distancia r del eje, según la fórmula [15] (página 74), es:

$v={\frac {2\pi r}{T}}$.

Así, pues, la aceleración hacia el eje, que designamos con k, es (véase pág. 74):

$k={\frac {4\pi ^{2}r}{T^{2}}}$

Ahora bien; si un cuerpo tiene con respecto a S la aceleración b, su aceleración absoluta será b + k; y entonces, como antes en el caso del movimiento rectilíneo acelerado, resulta la existencia de una fuerza aparente de la cantidad absoluta

$mk=m{\frac {4\pi ^{2}r}{T^{2}}},$[27]

dirigida en dirección que se aleja del eje del movimiento giratorio. Esta es la fuerza centrífuga.

fig42

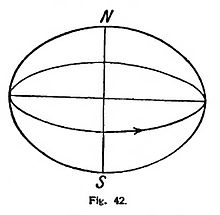
Sabido es que, entre las pruebas de la rotación de la Tierra, también representa un papel la fuerza centrífuga (figura 42). Empuja las masas lejos del eje de rotación, y de esta N suerte produce, en primer término, el achatamiento de la Tierra en los polos y, en segundo término, la disminución de la gravedad desde el polo al ecuador. Este último fenómeno lo conocimos ya cuando hablamos de la elección de una unidad de fuerza (II, 15, pág. 63); pero no nos ocupamos entonces de su causa. Según Newton, es una prueba de la rotación de la Tierra; la fuerza centrífuga que se dirige hacia fuera actúa en contra de la gravedad y disminuye el peso; en el ecuador, la disminución de la aceleración de la gravedad, g, es:

${\frac {4\pi ^{2}a}{T^{2}}}$

siendo a el radio terrestre.

Si aquí se le da a a el valor ya indicado más arriba (III, 3, fórmula [20], pág. 76) de 6,37 · 10⁸ cm., y a la duración de la rotación

T = un dia = 24 · 60 · 60 sec. = 86.400 sec.

se obtiene, para la aceleración de la gravedad, una diferencia entre el polo y el ecuador que vale

3,37 cm./sec²,

cantidad relativamente pequeña con relación a 981; este valor hay que aumentarlo un poco más por causa del aplastamiento de la Tierra.

Según la teoría de Newton sobre el espacio absoluto, hay que concebir estos fenómenos de tal suerte que no obedecen al movimiento relativo a otras masas, por ejemplo, las estrellas fijas, sino al movimiento de rotación absoluto en el espacio vacío. Si la Tierra estuviese inmóvil y todo el cielo de las estrellas fijas girase alrededor de la Tierra en veinticuatro horas, no se presentarían, según Newton, fuerzas centrífugas en la Tierra; la Tierra no estaría aplastada por los polos, y la gravedad sería en el ecuador la misma que en el polo. El aspecto del movimiento del cielo, visto desde la Tierra, seguiría siendo el mismo; y, sin embargo, entre ambos casos hay una diferencia determinada, físicamente comprobable.

fig43

Aun más claramente se ve esto en el experimento del péndulo de Foucault (1850). Un péndulo que oscila en un plano debe, según las leyes de la dinámica de Newton, conservar continuamente su plano de oscilación en el espacio absoluto, si se excluyen todas las fuerzas capaces de desviarlo. Si el péndulo se cuelga en el polo Norte, continúa la Tierra dando vueltas en cierto modo debajo de él (fig. 43); el observador sobre la Tierra observa, pues, una rotación del plano de oscilación en el sentido opuesto. Si la Tierra estuviese inmóvil, pero se moviese el cielo de las estrellas fijas, no podría, según Newton, cambiar el plano de oscilación del péndulo con respecto a la Tierra. Pero como cambia, ello demuestra una vez más la rotación absoluta de la Tierra.

Vamos a considerar otro ejemplo: el movimiento de la Luna alrededor de la Tierra (figura 44). Según Newton, la Luna vendría a caer sobre la Tierra si no tuviera en torno a ésta una rotación absoluta. Representémonos un sistema de coordenadas cuyo punto cero sea el centro de la Tierra, cuyo plano, x y, sea la trayectoria de la Luna y cuyo eje, x pase constantemente por la Luna. Si este sistema estuviese en reposo absoluto, sólo actuaría sobre la Luna la fuerza de la gravitación hacia el centro de la Tierra; según la fórmula [23] (pág. 82), tiene el valor

$K=k{\frac {Mm}{r^{2}}}$

La Luna caería sobre la Tierra a lo largo del eje x. Si no lo hace, es porque la rotación del sistema de coordenadas xy es absoluta y crea una fuerza centrífuga que mantiene en equilibrio la fuerza K. Tenemos:

${\frac {mv^{2}}{r}}=k{\frac {Mm}{r^{2}}}$

Esta fórmula no es otra cosa, naturalmente, que la tercera ley de Keplero; pues si se elimina la masa de la Luna, m, y se expresa v por el tiempo de revolución, T, a saber:

$v={\frac {2\pi r}{T}}$,

se obtiene:

${\frac {4\pi ^{2}r}{T^{2}}}={\frac {kM}{r^{2}}}$,

o, según la fórmula [22] (pág. 78):

${\frac {r^{3}}{T^{2}}}={\frac {kM}{4\pi ^{2}}}=C$

Otro tanto rige, naturalmente, también para la rotación de los planetas alrededor del Sol.

Este y muchos otros ejemplos muestran que la teoría newtoniana del espacio absoluto se apoya en hechos muy concretos. Si recorremos de nuevo la serie de los pensamientos, vemos lo que sigue:

El ejemplo del vaso de agua en movimiento de rotación demuestra que la rotación relativa del agua respecto al vaso no es la causa de que se manifiesten fuerzas centrífugas. Podría ser que fuesen la causa grandes masas circundantes, por ejemplo, la Tierra entera. El aplastamiento de la Tierra, la disminución de la gravedad en el ecuador, el experimento del péndulo de Foucault, muestran que la causa hay que buscarla fuera de la Tierra. Mas las trayectorias de todos los satélites y planetas no existen sino merced a fuerzas centrífugas que mantienen el equilibrio con la gravitación. Y, por último, se observa el mismo fenómeno en las más lejanas estrellas dobles, cuya luz necesita miles de años para llegar hasta nosotros. Parece, pues, que la presencia de fuerzas centrífugas es universal y no puede obedecer a efectos recíprocos. Por eso no hay sino admitir como su causa el espacio absoluto.

Estas conclusiones, desde Newton, han tenido una validez general. Pocos pensadores se han opuesto a ellas. Ante todo, y casi como único, cabe citar a Ernesto Mach; éste, en su Exposición crítica de la mecánica, ha analizado los conceptos de Newton y examinado su fuerza cognoscitiva. Parte del hecho que la experiencia mecánica no puede nunca enseñarnos nada acerca del espacio absoluto; lo único determinable, lo único, pues, que tiene físicamente realidad, son lugares relativos, movimientos relativos. Por eso las pruebas de Newton para demostrar la existencia del espacio absoluto deben de ser pruebas aparentes, falaces. En realidad, todo consiste en que se concede o no que, en el caso de una rotación del cielo entero en torno a la Tierra, no se presentarían ni el aplastamiento ni la disminución de la gravedad en el ecuador, etc. Con razón dice Mach que tales afirmaciones exceden con mucho a toda experiencia posible, y le reprocha con gran energía a Newton el haber traicionado en esto su propio principio de no admitir mas que hechos. Mach ha intentado incluso salvar la mecánica de ese grosero defecto de belleza. Pensó que había que concebir las fuerzas de inercia como efectos de las masas todas del universo, y bosquejó una dinámica nueva, en la que sólo entran fuerzas relativas. Mas su ensayo no podía tener buen éxito; por una parte, no comprendió lo que significa la relación entre inercia y gravitación, que es manifiesta en la proporcionalidad del peso y la masa; y, además, faltábale la teoría de la relatividad de los fenómenos ópticos y electromagnéticos, que aparta el prejuicio del tiempo absoluto. Ambas cosas han sido necesarias para el establecimiento de la nueva mecánica; ambas las ha llevado a cabo Einstein.