La teoría de la relatividad de Einstein/IV

IV

LAS LEYES FUNDAMENTALES DE LA OPTICA

1. El éter.

La mecánica es, histórica y objetivamente, el fundamento de la física; pero no es mas que una parte, una pequeña parte, de la física. Hasta ahora sólo hemos acudido a experiencias y teorías mecánicas para resolver el problema del espacio y del tiempo; ahora hemos de inquirir lo que las otras ramas de la investigación científica nos enseñan sobre ese punto.

En relación con el problema del espacio hállanse principalmente la óptica, la electricidad y el magnetismo. La razón es porque la luz y las fuerzas eléctricas y magnéticas surcan el espacio vacío. Los vasos donde se ha hecho el vacío máximo posible dan, sin embargo, paso a la luz; las fuerzas eléctricas y magnéticas actúan igualmente en el vacío. La luz del Sol y de las estrellas llega a nosotros a través del espacio cósmico vacío; las conexiones entre las manchas del Sol y las auroras boreales y las tormentas magnéticas muestran, sin teoría alguna, que los efectos electromagnéticos atraviesan el espacio cósmico. Este hecho de que ciertos procesos físicos se propagan por el espacio cósmico condujo bien pronto a la hipótesis de que el espacio no está vacío, sino lleno de una materia extraordinariamente fina, imponderable, el éter, que sería portador de esos fenómenos. Y hasta donde hoy se usa ese concepto de éter, entiéndese por tal no otra cosa que el espacio vacío, pero con ciertos estados físicos o «campos». Si quisiéramos desde un principio atenernos a tal conceptuación, tan abstracta, permanecería para nosotros incomprensible la mayor parte de los problemas que históricamente se enlazan con el éter. Este ha valido enteramente, como materia real, no sólo provista de estados físicos, sino capaz también de realizar movimientos.

Vamos a exponer la evolución de los principios, primero de la óptica, luego de la electrodinámica; ambos se unen bajo el nombre de física del éter. De esta suerte nos alejaremos un tanto, al principio, del problema del espacio y el tiempo, para luego volverlo a acometer con nuevas experiencias y leyes.

2. Teoría de la emisión y de la ondulación.

Digo, pues, que las superficies de los cuerpos
Envían figuras sutiles, copias de las cosas mismas.
........ Y tienen las imágenes
Que recorrer en tiempo imperceptible inmensurables distancias
.... Mas como sólo con los ojos podemos ver,
Por eso sucede que sólo de allí adonde los ojos se vuelven
Son éstos heridos por la figura y color de las cosas.

Estas palabras pueden leerse en el poema didáctico de Tito Lucrecio Caro acerca de la naturaleza de las cosas, en esa poética exposición de la filosofía epicúrea que fué escrita en el último siglo antes de Jesucristo.

Los versos citados contienen una especie de teoría de la emisión de la luz, que el poeta desenvuelve con una fantasía y al propio tiempo con un porte completamente científico. Y, sin embargo, no podemos señalar como teorías científicas ni esta teoría ni otras especulaciones de los antiguos sobre la luz; faltóles todo intento de determinar cuantitativamente los fenómenos, primer carácter de una objetivación. En los fenómenos luminosos es también particularmente difícil separar la sensación luminosa subjetiva del proceso físico y hacer mensurable este último.

La óptica científica puede decirse que comienza con Descartes. Su Dióptrica (1638) contiene las leyes fundamentales de la propagación de la luz, la ley de la reflexión y de la refracción; la primera era ya conocida entre los antiguos; la segunda acababa de ser descubierta experimentalmente por Snellius (hacia 1618). Descartes desenvolvió una representación del éter como portador de la luz, que resulta un precedente de la teoría de la ondulación. Esta se halla indicada ya en Roberto Hooke (1667); formúlala claramente Christian Huygens (1678), y su gran contemporáneo, un poco más joven, Newton, pasa por ser el inventor de la opinión opuesta: la teoría de la emisión. Antes de entrar en la lucha que esas dos teorías mantienen, vamos a explicar su esencia en pocos rasgos.

La teoría de la emisión afirma que de los cuerpos luminosos se desprenden corpúsculos finísimos que se mueven según las leyes de la mecánica, y al tropezar con el ojo producen la sensación luminosa.

fig45

La teoría de la ondulación pone la propagación de la luz en analogía con el movimiento de las ondas en una superficie de agua o con las ondas sonoras en el aire. Tiene que admitir para ello que existe un medio que atraviesa todos los cuerpos transparentes y puede verificar ondulaciones, vibraciones; éste es el éter lumínico. Las partecillas singulares de esta substancia muévense pendularmente alrededor de sus posiciones de equilibrio; lo que como onda luminosa se propaga es el estado de movimiento de esas partes, mas no las partes mismas. El dibujo (fig. 45) muestra el proceso en una serie de puntos que pueden oscilar de arriba abajo. Cada una de las curvas dibujadas una debajo de otra corresponde a un momento; por ejemplo, t = 1, 2, 3..... Cada punto realiza un movimiento de oscilación vertical; todos los puntos juntos presentan el aspecto de una onda que por momentos prospera hacia la derecha.

Mas hay una razón importante en contra de la teoría ondulatoria. Es sabido que las olas rodean los obstáculos; puede esto observarse en toda superficie de agua, y asimismo el sonido «da la vuelta a la esquina». En cambio, un rayo de luz se propaga en linea recta; si en su camino ponemos un cuerpo opaco de aristas afiladas, obtendremos una sombra muy marcadamente limitada.

Este hecho fué causa de que Newton rechazase la teoría de la ondulación. No se decidió claramente por una hipótesis determinada, y estableció tan sólo que la luz es algo que se mueve alejándose del cuerpo luminoso, con determinada velocidad, «como corpúsculos lanzados». Pero sus sucesores han interpretado su opinión en favor de la teoría de la emisión, y la autoridad de su nombre ha hecho que ésta impere durante un siglo entero. Sin embargo, en su tiempo (1665) había ya descubierto Grimaldi que la luz puede «doblar la esquina»; junto a los limites de la sombra, vese, en efecto, una débil iluminación del espacio sombreado, que afecta la forma de rayas, fenómeno que se llama difracción de la luz. Este descubrimiento fué el que hizo de Huygens un celoso defensor de la teoría ondulatoria; como primero y más importante argumento en favor de ella, consideraba el hecho de que dos rayos de luz se cruzan sin influir uno sobre el otro, como dos cursos de ondulaciones sobre el agua, mientras que dos haces de partículas emitidas habrían de chocar, o al menos perturbaríanse uno a otro. Huygens consiguió explicar la reflexión y la refracción fundándose en la teoría ondulatoria; para ello le sirvió el principio, que hoy lleva su nombre, según el cual todo punto que recibe una excitación luminosa ha de considerarse a su vez como fuente de una onda luminosa de forma esférica. Sobre esto se produjo una diferencia fundamental entre la teoría de la emisión y la de la ondulación, que resolvió más tarde en favor de la última la experimentación decisiva.

fig45

Es sabido que un rayo de luz que viniendo del aire llega a la superficie plana de un cuerpo más denso, como vidrio o agua, es refractado de suerte que sigue su marcha por el cuerpo en dirección más próxima a la perpendicular sobre la superficie del mismo (fig. 46). La teoría de la emisión explica esto admitiendo que las partículas luminosas, en el momento de penetrar en el medio más denso, sufren una atracción de éste; reciben, pues, una aceleración en la superficie del cuerpo, en dirección perpendicular a ésta, y por eso son desviadas hacia dentro.

fig45

De aquí se sigue que en el medio más denso deben moverse más aprisa que en el menos denso. La construcción de Huygens, según la teoría ondulatoria, descansa exactamente en la hipótesis inversa (fig. 47). La onda luminosa, al llegar a la superficie, produce en cada uno de sus puntos ondas elementales; si éstas se propagan en el segundo medio, que es más denso, con mayor lentitud, resultará que el plano que toca a todas esas ondas esféricas, y que, según Huygens, representa la onda refractada, queda desviado en exacto sentido.

fig45

fig45

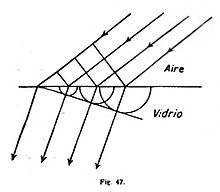
Huygens interpretó también la doble refracción del espato de Islandia, descubierto en 1669 por Erasmo Bartholino. Fundóse para ello en la teoría ondulatoria, admitiendo que la luz en el cristal puede propagarse con dos velocidades distintas, de suerte que una onda elemental sea una esfera y la otra un esferoide. Descubrió el notable fenómeno de que los dos rayos luminosos que salen de un pedazo de espato se comportan frente a un segundo pedazo de espato por modo muy diferente que la luz ordinaria; si al segundo cristal se le hace girar en torno a un rayo que salga del primero, prodúcense de él, según la posición, dos rayos de cambiante fuerza, uno de los cuales puede desaparecer por completo (fig. 48). Newton advirtió (1717) que de aquí hay que concluir que un rayo luminoso, en su simetría, no corresponde a un prisma de sección circular, sino cuadrada; interpretó este hecho en contra de la teoría ondulatoria, pues en aquel tiempo pensábanse las ondas luminosas por analogía con las ondas sonoras, como ondas de densificación y rarefacción, en las cuales las partículas oscilan en la dirección de la propagación de la onda, «longitudinalmente» (fig. 49), y es claro que ésta ha de tener simetría giratoria en torno a la dirección de la propagación.

3. La velocidad de la luz.

Independientemente de la discusión entre ambas hipótesis sobre la naturaleza de la luz, realizáronse las primeras determinaciones de su más importante propiedad, la que va a ser el centro de nuestras consideraciones siguientes, a saber: la velocidad de la luz. De todas las experiencias sobre propagación de la luz resultaba ya que esa velocidad tenia que ser enorme; Galileo intentó medirla por medio de linternas de señales, pero sin éxito, pues las distancias terrestres las recorre la luz en tiempos extraordinariamente pequeños. Por eso la medición no tuvo éxito hasta que se emplearon las distancias enormes que median entre los astros en el espacio cósmico.

Olaf Roemer observó (1676) que los eclipses regulares de los satélites de Júpiter se adelantan o se atrasan, según que la Tierra está más lejos o más cerca de Júpiter (fig. 50); interpretó este fenómeno por la diferencia de tiempo que la luz necesita para recorrer diferentes distancias, y calculó la velocidad de la luz. Designarémosla siempre con la letra c; su valor exacto, al que Römer se acercó mucho, es

$c=300000km./sec.=3\cdot 10^{1}0cm./sec.$[28]

Otro efecto de la velocidad de la luz descubrió James Bradley (1727), a saber: que todas las estrellas fijas parecen verificar al año un movimiento común, que, evidentemente, reproduce la revolución de la Tierra alrededor del Sol. El origen de este efecto es muy fácil de explicar desde el punto de vista de la teoría de la emisión; vamos a exponer aquí esta interpretación; pero debemos observar que precisamente este fenómeno ocasiona a la teoría ondulatoria dificultades de que más tarde habremos de hablar. Ya sabemos (III, 7, pág, 86) que un movimiento que es rectilíneo y uniforme en un sistema de referencia S, lo es también en S' si éste verifica un movimiento de traslación con respecto a S; pero la cantidad y la dirección de la velocidad son distintas en ambos sistemas. De aqui se sigue que un torrente de partículas luminosas que viene de una estrella fija y llega a la Tierra, parece provenir de otra dirección. Vamos a considerar particularmente esta desviación o aberración para el caso en que la luz llega perpendicular al movimiento de la Tierra (fig. 51). Al llegar una partícula luminosa al objetivo de un telescopio, supongamos que éste se halla en la posición 1; mientras la luz recorre la longitud l del telescopio, la Tierra con el telescopio en ella, pasa a ocupar la posición 2, a la distancia d de la posición 1; el rayo alcanza, pues, el centro del ocular, cuando ya no procede de la dirección del eje del telescopio, sino de otra dirección un poco apartada de la primera en el sentido del movimiento de la Tierra. La dirección de la visión no señala, pues, el verdadero lugar de la estrella, sino otro lugar del cielo un poco desviado hacia delante. El ángulo de desviación queda determinado por la relación d : l y se ve que depende de la longitud del telescopio; pues si esta longitud aumenta, aumenta el tiempo que necesita la luz para recorrerlo y, por tanto, también la distancia el recorrida por la Tierra durante ese tiempo. Es evidente que las distancias l y d, recorridas en un mismo tiempo por la luz y por la Tierra, son entre sí como las velocidades correspondientes:

${\frac {d}{l}}={\frac {v}{c}}$

Esta proporción, llamada también constante de aberración, la designaremos en adelante con la letra β:

$\beta ={\frac {v}{c}}$[29]

Tiene un valor numérico muy pequeño, pues la velocidad de la Tierra en su trayectoria alrededor del Sol vale aproximadamente v = 30 km./sec, mientras que, como ya dijimos, la velocidad de la luz c = 300.000 km./sec; por donde resulta β igual a 1/10.000.

Las posiciones aparentes de todas las estrellas fijas están, pues, algo desplazadas en la dirección del movimiento momentáneo de la Tierra y describen, por tanto, durante la anual revolución de la Tierra alrededor del Sol, una pequeña figura elíptica. Midiéndola es posible hallar la relación β, y como la velocidad de la Tierra en su trayectoria es conocida por datos astronómicos, puede determinarse la velocidad de la luz c. El resultado coincide bien con la medición de Römer.

fig52

Ahora anticipemos la evolución histórica, y hablemos de las mediciones de la velocidad de la luz verificadas en la Tierra. Para ello no hace falta, en principio, nada más que un método técnico de medir con certeza los tiempos extraordinariamente pequeños que la luz necesita para recorrer distancias terrestres de pocos kilómetros, y a veces hasta de metros. Ficeau (1849) y Foucault (1865) han realizado estas mediciones con dos métodos diferentes y han confirmado el valor de c, que se determina por métodos astronómicos. No es preciso explicar aquí los detalles de esos métodos, que se encuentran, además, en cualquier libro elemental de física. Sólo llamaremos la atención sobre un punto: en ambos métodos el rayo luminoso es lanzado desde su origen a un espejo S, en donde es reflejado y vuelve a su punto de partida (fig. 52). Recorre, pues, el camino dos veces, y lo que se mide, por tanto, es solamente la velocidad media en la ida y vuelta. Esto tiene una consecuencia importante para nuestras reflexiones posteriores: suponiendo que la velocidad de la luz no sea igual en las dos direcciones, por la razón de que la Tierra misma se mueve—ya volveremos sobre esto más detalladamente—, este influjo se reducirá totalmente o casi totalmente en la ida y vuelta del rayo. Por eso no hace falta tener en cuenta en la práctica el movimiento de la Tierra, en estas mediciones, dada la pequeñez de la velocidad de la Tierra comparada con la de la luz.

Las mediciones de la velocidad de la luz se han repetido más tarde con medios más completos, y han llegado a tener una considerable exactitud; hoy pueden llevarse a cabo en una habitación de mediano tamaño. El resultado es el ya indicado en la fórmula [28]. Con el método de Foucault podía también medirse la velocidad de la luz en el agua; encontróse que es más pequeña que en el aire. Así quedó decidida una de las cuestiones mas importantes que debatían las teorías de la emisión y de la ondulación, en favor de esta última; pero ya en un tiempo en que la victoria de la teoría ondulatoria estaba asegurada hacia tiempo.

4. Conceptos fundamentales de la teoría ondulatoria. Interferencia.

El gran descubrimiento de Newton en la óptica fué el análisis de la luz blanca; su división en elementos coloreados, con la ayuda de un prisma, y la exacta investigación del espectro: todo lo cual le condujo a la convicción de que los colores del espectro son las partes indivisibles de la luz. Fué el fundador de la teoría del color, cuyo contenido físico está aún hoy—a pesar de los ataques de Goethe—en completa vigencia. El torrente de los descubrimientos de Newton paralizó la vista de las generaciones posteriores. Su negativa a admitir la teoría de la ondulación cerró a esta hipótesis el camino durante cien años. Sin embargo, halló partidarios aislados, y entre éstos, en el siglo xviii, el gran matemático Leonardo Euler.

La resurrección de la teoría ondulatoria se debe a los trabajos de Tomás Young (1802), el cual acudió al principio de la interferencia para explicar los anillos y las franjas coloreadas, que ya Newton había observado en capas finas de substancias transparentes. Vamos a ocuparnos en este lugar con algún detalle del proceso de interferencia, porque en todas las mediciones ópticas finas, y sobre todo en las investigaciones que sirven de fundamento a la teoría de la relatividad, tiene un papel decisivo.

Ya hemos explicado la esencia de la onda; consiste en que las partículas de un cuerpo verifican oscilaciones periódicas alrededor de sus posiciones de equilibrio, siendo diferente la posición momentánea o fase de movimiento de las partículas vecinas y corriéndose hacia adelante con velocidad constante. El tiempo que una partícula determinada necesita para realizar una oscilación o vibración completa de ida y vuelta llámase duración o período de vibración, y se caracteriza con la letra T. El número de vibraciones en un segundo o frecuencia de las mismas lo designaremos con ν. Como la duración de una vibración, multiplicada por su frecuencia, o sea por el número de ellas en un segundo, debe dar justamente un segundo entero, tendremos que νT = 1; es decir:

$\nu =frac{1}{T}$o<math>T=\frac{1}{\nu}[30]

fig53

En lugar de «número de vibraciones» se dice muchas veces también «color», porque una onda luminosa de determinado número de vibraciones produce en el ojo una determinada sensación de color. No nos ocuparemos del problema complicado de cómo la gran muchedumbre de las impresiones psicológicas de color se produce por la acción conjunta de sencillas vibraciones periódicas o «colores físicos». Las ondas que parten de una pequeña fuente luminosa tienen la forma de esferas; esto significa que todas las partículas en una esfera alrededor del foco luminoso se encuentran siempre en igual estado de vibración o en la misma «fase» (fig. 53). Por refracción u otra influencia cualquiera, puede una parte de tal onda esférica deformarse, de suerte que las superficies de igual fase o superficies de onda tengan alguna otra forma. La más sencilla superficie de onda es evidentemente el plano; y es claro que un trozo suficientemente pequeño de una superficie cualquiera de onda, aunque sea de una onda esférica, puede considerarse siempre por aproximación como plano. Consideraremos, pues, principalmente la propagación de ondas planas (fig. 54). La dirección perpendicular a los planos de onda, o sea la normal de onda, es al mismo tiempo la dirección de propagación; bastará, pues, considerar el estado de vibración a lo largo de una recta paralela a esa dirección.

fig54

Dejaremos aún intacta la cuestión de saber si la vibración de cada partícula es paralela o perpendicular a la dirección de la propagación, y de si es longitudinal o transversal. En las figuras dibujamos siempre lineas de onda, y llamamos a las posiciones extremas de la oscilación, según que sean hacia arriba o hacia abajo, cumbres o valles de las ondas.

La distancia de una cumbre a la próxima llámase longitud de onda y se designa con λ. Evidentemente, la distancia entre dos valles sucesivos es igual, y también lo es la que separe a dos planos próximos de igual fase.

Durante una oscilación de ida y vuelta de una determinada partícula, cuya duración es T, avanza la onda justamente una longitud de onda λ (fig. 45, pág. 105).

Mas como para todo movimiento es la velocidad la relación entre el camino recorrido y el tiempo empleado, será la velocidad c de la onda igual a la relación de la longitud de la onda con la duración de la vibración:

$c={\frac {\lambda }{T}}$ o $c=\lambda \nu$[31]

Cuando una onda pasa de un medio a otro, por ejemplo, del aire al vidrio, trasládase, naturalmente, a través del limite el ritmo temporal de las vibraciones; por tanto, T (ó ν) permanece lo mismo. En cambio, varia la velocidad c y, por tanto, según la fórmula [31], también la longitud de onda l. Todos los métodos para medir l pueden servir, por tanto, para comparar las velocidades de la luz en diferentes substancias o en diferentes circunstancias. De esto haremos uso muchas veces más adelante.

Ya ahora podemos comprender la esencia de los fenómenos de interferencia, cuyo descubrimiento ha dado la victoria a la teoría ondulatoria. Puede describirse la interferencia con las palabras siguientes, que suenan a paradoja: luz añadida a luz no da necesariamente más luz, sino que puede también apagarse.

fig55

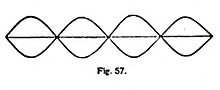
El fundamento es que, según la teoría ondulatoria, la luz no es un torrente de partículas materiales, sino un estado de movimiento; dos impulsos de movimiento que se encuentran pueden, empero, aniquilar el movimiento, como dos hombres que quieren lo contrario se contraponen y no logran conseguir nada. Representémonos dos trenes de ondas que se cruzan. Puede observarse este proceso con gran belleza mirando a un lago desde una altura y viendo cómo se encuentran las estelas producidas por dos embarcaciones (fig. 55). Estos dos sistemas de ondas se cruzan sin perturbarse; en el territorio en donde están los dos a la vez nace un movimiento complicado; pero tan pronto como una onda ha atravesado la otra, sigue su camino, como si nada le hubiese pasado. Si se considera el movimiento de una partícula en vibración, resulta que ésta recibe de las dos ondas impulsos de movimiento independientes; su oscilación es, pues, en cada momento, simplemente la suma de las oscilaciones que tendría estando bajo el influjo de cada onda. Se dice que dos movimientos ondulatorios se superponen sin perturbarse. De aquí se sigue que allí donde, al encontrarse dos ondas iguales, coinciden las cumbres con las combres y los valles con los valles, se produce una duplicación de las elevaciones y de las profundidades (fig. 56); pero si las cumbres tropiezan con los valles, anúlanse los impulsos y no se produce ninguna vibración (fig. 57).

fig56

fig57

Si se quieren observar interferencias, no se debe tomar simplemente dos focos de luz y hacer que se crucen los trenes de ondas que emiten; de este modo no se produce ningún fenómeno observable de interferencia, porque las verdaderas ondas luminosas no son ondas absolutamente regulares. El estado de vibración cambia de pronto después de una serie de vibraciones regulares, y ese cambio es casual, correspondiendo a los procesos casuales al verificarse la emisión de la luz en la fuente luminosa; estos cambios irregulares producen una variación correspondiente en los fenómenos de interferencia, que se verifica harto de prisa para que el ojo pueda seguirla, y así resulta que se ve solamente una luz regular.

Para obtener interferencias observables hace falta dividir un rayo luminoso en dos rayos, por métodos artificiales, por reflexión y refracción; luego se procura que esos dos rayos se encuentren. De esta manera las irregularidades de las vibraciones tienen en ambos rayos el mismo ritmo de tiempo, y, por tanto, los fenómenos de interferencia no vacilan en el espacio, sino que permanecen fijos; donde las ondas en un momento se aviven o se apaguen, allí lo harán siempre.

Se dirige la vista, armada con lupa o con anteojo, a ese punto, y si se ha usado luz de un solo color, como, por ejemplo, la luz de una llama de Bunsen, coloreada de amarillo con sal, se ven manchas claras y obscuras, rayas y anillos. Si se trata de luz ordinaria, compuesta de muchos colores, las manchas de interferencia correspondientes a las diferentes longitudes de onda no coinciden todas; en un punto acaso sea avivado el rojo, apagado el azul; en otro punto sucederá otra cosa, y asi se producen manchas y rayas con maravillosos aspectos de color. Pero nos apartaríamos de nuestro camino si siguiéramos ocupándonos de tan interesantes fenómenos.

Las más sencillas disposiciones para la producción de interferencias las encontró Fresnel (1822), un investigador cuyos trabajos dan la base para la teoría de la luz, tal como ha regido, sin objeciones, hasta nuestros días. Muchas veces hemos de encontrar su nombre. Esa época de los primeros decenios del siglo xix debe de haber sido, en muchos sentidos, semejante a la de hoy. Así como hoy, por el descubrimiento de la radioactividad y los fenómenos afines de irradiación, por el establecimiento de la teoría de la relatividad y la teoría de los quenta, está realizándose un formidable progreso, en extensión y profundidad, de nuestro conocimiento natural, que para el que está fuera aparece como una revolución de todos los conceptos recibidos, así también hace cien años los millares de observaciones aisladas, ensayos teóricos, especulaciones físicas o metafísicas, se organizaron por vez primera en representaciones y teorías cerradas, unitarias, cuya aplicación ocasionó al punto una insospechada abundancia de nuevas observaciones y experimentos. En esa época se produjo la «Mecánica analítica» de Lagrange, la «Mecánica celeste» de Laplace, dos obras que llevan a término las ideas de Newton; de ellas salió por una parte la mecánica de los cuerpos deformables, la teoría de los líquidos y substancias elásticas entre las manos de Navier, Poisson, Cauchy, Green; por otra parte, los trabajos de Young, Fresnel, Arago, Malus, Brewster establecieron la teoría de la luz. Al mismo tiempo empezó la era de los descubrimientos electromagnéticos, de que más tarde hablaremos. Entonces la investigación física estaba casi exclusivamente en las manos de los franceses, ingleses, italianos. Hoy todas las naciones cultas colaboran en la obra común, y los creadores de las grandes teorías de la relatividad y de los quanta, Einstein y Planck, son alemanes.

fig58

fig59

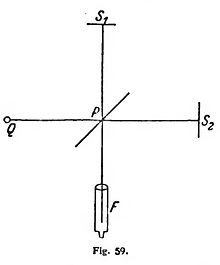
Fresnel proyecta un rayo luminoso sobre dos espejos levemente inclinados uno sobre otro S₁ y S₂ (fig. 58); el rayo se refleja, y los dos rayos reflejados producen, en el punto en que se encuentran, rayas de interferencia que se pueden ver con una lupa. Se han indicado análogas disposiciones en gran número. Sólo nos ocuparemos aquí de una esfera de aplicación, que es importante para nuestro propósito, a saber: métodos experimentales para medir pequeñas variaciones de la velocidad de la luz. Estos aparatos se llaman interferómetros. Se fundan en el hecho de que con la velocidad de la luz se altera también la longitud de onda, y así las interferencias se desplazan. Un aparato de esta clase es el interferómetro de Michelson, el físico de la Universidad de Chicago. Consiste esencialmente (fig. 59) en una lámina de vidrio P, que está plateada para ser semitransparente, de manera que deja pasar la mitad del rayo emitido por el foco luminoso Q y refleja la otra mitad. Esos dos rayos se dirigen a dos espejos S₁ y S₂, son allí reflejados y pasan de nuevo por la lámina semitransparente P, que los vuelve a dividir y envía la mitad de cada uno al anteojo observador F. Si las dos dimensiones PS₁ y PS₂ son iguales, entonces los dos rayos llegan al anteojo con la misma fase de vibración y se componen formando de nuevo la luz primitiva; pero si, desplazando el espejo S₁ y se alarga el camino que ha de recorrer el primer rayo, ya al juntarse ambos en F no coinciden las cumbres con las cumbres y los valles con los valles, sino que están desplazados unos con respecto a otros y se debilitan más o menos. Si el espejo S₁ se mueve lentamente, vense, pues, en el anteojo F, alternativamente, claridades y obscuridades; la distancia entre las posiciones de S₁ para dos obscuridades sucesivas es exactamente igual a la longitud de onda de la luz. De esta manera, Michelson ha medido longitudes de onda con precisión que es superior a casi todas las demás mediciones físicas. Ello se consigue contando los cambios de obscuridad y claridad que se producen cuando el espejo S₁ y ha sufrido un desplazamiento notable, que comprende muchos miles de longitudes de onda; el error de observación de una longitud de onda queda de ese modo reducido en miles de veces.

Es éste el momento de dar algunas cifras. Por el método descrito se encuentra que la longitud de onda en la luz amarilla, producida coloreando de amarillo la llama de Bunsen con sal común y cuyo foco son los átomos de cloruro sódico, es en el vacío

${\frac {5}{10000}}{\text{mm.}}=5\cdot 10^{-5}{\text{cm.}}$

Toda luz visible está comprendida entre las longitudes de onda 4·10^-5 cm. para el violeta y 8·10^-5 cm. para el rojo. La extensión de la luz visible comprende, pues, en lenguaje de la acústica, una octava, esto es, desde una longitud de onda a otra longitud doble. Por la fórmula [31] se deriva que el número de vibraciones de la luz amarilla tiene el enorme valor de

$\nu ={\frac {c}{\lambda }}={\frac {3\cdot 10^{10}}{5\cdot 10^{-5}}}=6\cdot 10^{14}$,

o sean 600 billones de vibraciones por segundo. Las más rápidas vibraciones sonoras perceptibles son de 50.000 por segundo.

La extraordinaria exactitud de las mediciones ópticas descansa en la multiplicación de las longitudes de onda que se aplica en las medidas interferométricas. Se puede, por ejemplo, determinar que la velocidad de la luz varia en un gas a consecuencia de levísimas variaciones de presión o de temperatura (por ejemplo, al tocar el aparato con la mano). Para ello se pone el gas en un tubo entre la lámina de vidrio P y el espejo S₁, y entonces se ven, al más pequeño aumento de presión, cómo varían las interferencias, cómo claridades se deshacen con obscuridades.

Por lo demás, debemos advertir que en el interferómetro generalmente no se ven sólo campos claros y obscuros, sino un sistema de anillos claros y obscuros. Esto proviene de que los dos rayos no son exactamente paralelos, y las ondas no son exactamente planas; las partes de ambos rayos tienen, pues, que recorrer caminos que no son iguales exactamente. Pero no nos entretendremos en detalles geométricos; sólo mencionaremos esta circunstancia porque suele hablarse de rayas o franjas de interferencia.

Volveremos a encontrar el interferómetro de Michelson cuando se trate de saber si el movimiento de la Tierra influye en la velocidad de la luz.

5. Polarización y transversalidad de las ondas luminosas.

Aun cuando los fenómenos de interferencia no admiten casi más interpretación que la de la teoría ondulatoria, sin embargo, hanse ofrecido dos dificultades para su reconocimiento universal. Estas dificultades, como ya hemos visto, han sido consideradas por Newton como decisivas: es la primera la propagación rectilínea de la luz, al menos en lo esencial (es decir, salvo los pequeños fenómenos de difracción); es la segunda la explicación de los fenómenos de polarización. La primera quedó resuelta por sí misma cuando la teoría ondulatoria fué perfeccionándose; se mostró, en efecto, que las ondas «doblan la esquina» sin duda, pero sólo en proporciones que son del mismo orden de magnitud de la longitud de onda. Como esta longitud es muy pequeña, resulta, para la observación grosera, la apariencia de sombras duras y rayos limitados por lineas rectas; una observación más fina es la que puede notar las franjas de interferencia de la luz difractada a lo largo del límite de la sombra. Fresnel, y más tarde Kirchhoff (1882), y recientemente Sommerfeld (1895), han hecho trabajos valiosísimos en la teoría de la difracción; han calculado los finos fenómenos de difracción y establecido los limites dentro de los cuales es licito operar con el concepto de rayo de luz.

La segunda dificultad refiérese a los fenómenos de la polarización de la luz.

Cuando se hablaba de ondas, entendíase entonces vibraciones longitudinales, como eran conocidas en el sonido; una onda sonora consiste efectivamente en condensaciones y dilataciones rítmicas, en las cuales la partícula de aire oscila en la dirección de la propagación de la onda. Conocíanse, sin duda, vibraciones transversales; por ejemplo, las ondas superficiales en el agua o las vibraciones de una cuerda tensa, en las que las partículas oscilan perpendicularmente a la dirección de la propagación de la onda. Pero aquí no se trata de ondas que se propagan en el interior de una substancia, sino de fenómenos en la superficie (ondas acuáticas), o de movimientos del cuerpo entero (vibraciones de la cuerda). No existían entonces observaciones ni teorías sobre la propagación de las ondas en cuerpos elásticos, fijos; esto explica el hecho, para nosotros extraño, de que se haya tardado tanto en reconocer que las ondas ópticas son vibraciones transversales. Es más: ocurrió el caso extraño de que el impulso para que se desarrollase la mecánica de los cuerpos elásticos, perceptibles a simple vista, procedió de experiencias y conceptuaciones sobre la dinámica del éter imponderable, imperceptible.

Ya hemos explicado en qué consiste la esencia de la polarización: los dos rayos luminosos que salen de un trozo de espato, que refracta un rayo en dos, no se comportan, al atravesar un segundo cristal semejante, como la luz ordinaria; no se dividen otra vez cada uno en dos rayos iguales, sino en desiguales rayos, uno de los cuales puede incluso, en ciertas circunstancias, desaparecer por completo. Es como si las diferentes direcciones dentro de un plano de onda no fueran de igual valor (fig. 60). Malus descubrió (1808) que la polarización no es una característica de la luz que atraviesa cristales de doble refracción, sino que puede ser producida por sencilla reflexión; mostró que una luz reflejada por un espejo bajo un ángulo determinado es reflejada por otro espejo con diferente fuerza, cuando se hace girar este espejo alrededor del rayo incidente (figura 61). El plano perpendicular a la superficie del espejo, el que contiene el rayo incidente y reflejado, llámase plano de incidencia; se dice entonces que el rayo reflejado está polarizado en el plano de incidencia, con lo cual se quiere decir no más sino que el rayo se comporta diferentemente, en una nueva reflexión, según esté el segundo plano de incidencia respecto del primero. Si los dos planos son perpendiculares, no se verifica reflexión alguna en el segundo espejo.

fig60

fig61

Los dos rayos que salen de un pedazo de espato están polarizados perpendicularmente uno a otro; si se dejan caer los dos sobre un espejo, buscando el ángulo adecuado, uno de ellos se apagará justamente en tal posición del espejo, mientras que el otro es reflejado en totalidad.

El experimento decisivo hiciéronlo Fresnel y Arago (1816), intentando hacer interferir dos de esos rayos polarizados perpendicularmente uno a otro. No consiguieron producir interferencias, y Fresnel, como asimismo Young, sacaron la consecuencia (1817) de que las vibraciones luminosas tienen que ser transversales.

fig62

Con esto se explica, en efecto, facilisimamente la peculiar conducta de la luz polarizada. Las vibraciones de una partícula de éter verifícanse, no en la dirección de la propagación, sino perpendicularmente a ella; esto es, en el plano de onda (fig. 60), todo movimiento de un punto en un plano puede, empero, concebirse como compuesto de dos movimientos en dos direcciones perpendiculares una a otra; ya hemos visto, al hablar de la cinemática de un punto, que el movimiento del mismo queda unívocamente determinado indicando las coordenadas rectangulares variables con el tiempo. Un cristal de doble refracción tiene, evidentemente, la propiedad de que en él las vibraciones de la luz se propagan en dos direcciones perpendiculares una a otra, con velocidad diferente; por tanto, según el principio de Huygens, al penetrar en el cristal son refractadas con diferente fuerza y, por tanto, separadas en el espacio. Cada uno de los dos rayos salientes consta, pues, de vibraciones que se verifican, para cada uno, en un plano determinado, que pasa por la dirección del rayo, y los dos planos pertenecientes a los dos rayos son perpendiculares (figura 62); dos vibraciones de éstas no pueden evidentemente influirse, no pueden interferir. Si ahora un rayo polarizado entra en un segundo cristal, no pasará por él sin debilitarse, a no ser que la dirección de su vibración tenga justamente, respecto del cristal, la posición exacta en que esa dirección de la vibración pueda propagarse; en todas las demás posiciones, el rayo se debilita, y en la dirección perpendicular o cruzada no pasa en absoluto.

fig63

Lo mismo sucede en la reflexión; si ésta se verifica en el ángulo adecuado, entonces, de las dos vibraciones paralelas y perpendiculares al plano de incidencia, una sola será reflejada, la otra penetra en el espejo y queda absorbida por él (fig. 63). No es posible, naturalmente, determinar si la vibración reflejada es la que oscila en el plano de incidencia o la que oscila perpendicularmente a él. Pero esta cuestión de la posición de la vibración con respecto al plano de incidencia o dirección de la polarización ha ocasionado muy amplias investigaciones, teorías y discusiones, como en seguida veremos.

6. El éter como cuerpo sólido elástico.

Conocida, pues, ya la transversalidad de las ondas luminosas y demostrada por numerosos experimentos, surgió a la consideración de Fresnel la imagen de una futura teoría dinámica de la luz, que habría de derivar, según el modelo de la mecánica, los fenómenos ópticos de las propiedades del éter y de las fuerzas actuantes en él. El éter tenia que ser, por tanto, una especie de cuerpo elástico, sólido; pues sólo en éste pueden verificarse ondas transversales mecánicas. Pero en la época de Fresnel no estaba aún desarrollada la teoría matemática de la elasticidad de los cuerpos sólidos; además, podía muy bien creer Fresnel que no era lícito exagerar a priori la analogía del éter con substancias materiales. En todo caso, prefirió inquirir empíricamente las leyes de la propagación de la luz e interpretarlas con la representación de las ondas transversales. Ante todo, debía esperarse que los procesos ópticos en cristales diesen explicación acerca de la conducta que observa el éter luminoso. Los trabajos de Fresnel en este punto pertenecen a las más bellas producciones de la metódica física, tanto en el sentido experimental como en el teórico; pero no debemos perdernos ahora en los detalles, y hemos de conservar la vista fija en nuestro problema: ¿cómo está constituido el éter luminoso?

Los resultados de Fresnel parecieron confirmar la analogía de las ondas luminosas con las ondas elásticas. Así recibió gran impulso la elaboración sistemática de la teoría de la elasticidad, que ya Navier (1821) y Cauchy (1822) habían iniciado, y a la que Poisson (1828) dedicó su esfuerzo. Cauchy aplicó en seguida a la óptica las leyes recién descubiertas de las ondas elásticas (1829). Vamos a intentar dar una representación del contenido ideal de esta teoría del éter.

La dificultad estriba en que el medio adecuado para describir variaciones en cuerpos continuos, deformables, es el método de las ecuaciones diferenciales. Mas no queriendo nosotros suponerlas conocidas del lector, no nos queda otro recurso que describir un ejemplo sencillo y añadir en conclusión: así, pero algo más complicado, es el caso general. El lector no avezado a las matemáticas llegará acaso a tener un concepto grosero de la cosa; pero lo que difícilmente obtendrá es una intuición de la fuerza y capacidad productiva de las imágenes físicas y del método matemático a ellas adecuado. Comprendemos muy bien la imposibilidad de satisfacer plenamente al no matemático; pero no podemos dejar de intentar una explicación de la mecánica de los continuos, porque todas las teorías siguientes, no sólo las del éter elástico, sino también la electrodinámica en todas sus formas, y sobre todo la teoría de la gravitación de Einstein, se apoyan en esas conceptuaciones.

Una cuerda fina muy tensa es, en cierto modo, una formación elástica de una dimensión; sobre ella vamos a desenvolver los conceptos de la teoría de la elasticidad. Para poder referirnos a la mecánica usual, que no conoce mas que cuerpos aislados y rígidos, pensemos la cuerda constituida, no por modo continuo, sino en cierta manera por átomos. Consta de una serie de corpúsculos iguales, ordenados en linea recta a iguales distancias sucesivamente (fig. 64). Las partículas tienen masa inerte, y cada una de ellas ejerce fuerzas sobre sus dos vecinas, las cuales están constituidas de suerte que resisten tanto a un aumento como a una disminución de la distancia. Si se quiere tener una imagen intuitiva de las tales fuerzas, supónganse en pequeños resortes de espiral entre los corpúsculos; estos resortes resistirían tanto a una compresión como a una tensión. Pero no debe tomarse a la letra esta imagen; las fuerzas de la especie que describimos son justamente el fenómeno primario de la elasticidad.

fig58

Si, pues, la primera partícula es desplazada un poco en el sentido longitudinal o latitudinal, actuará al punto sobre la segunda, y ésta transmitirá la acción a la tercera, y así sucesivamente. La perturbación del equilibrio en la primera partícula recorre, pues, la serie entera, a modo de una onda, y llega finalmente a la última partícula. Mas este proceso no se verifica con infinita velocidad, sino que en cada partícula hay una pérdida de tiempo, porque la partícula posee una masa inerte y no sigue inmediatamente el impulso recibido, pues la fuerza no produce un desplazamiento súbito, sino aceleración, esto es, una variación de velocidad durante un breve tiempo, y la variación de velocidad produce, con el tiempo también, un desplazamiento. Sólo cuando este desplazamiento existe en todo su valor, alcanza la fuerza sobre la partícula próxima su pleno valor, y el proceso va repitiéndose cada vez con una pérdida de tiempo que depende de la masa de las partículas. Si la fuerza que sale de la primera partícula al ser desplazada influyera directamente en la última partícula de la serie, el efecto se verificaría súbitamente. Tal sucede, según la teoría newtoniana de la gravitación, en las atracciones respectivas de los astros; la fuerza que uno ejerce sobre el otro está siempre dirigida al lugar momentáneo que el primero ocupa y determinada en cantidad por la distancia momentánea. Se dice que la gravitación de Newton es una acción a distancia, pues actúa en la lejanía sin la mediación del medio que separa los dos astros.

En cambio, nuestra serie de equidistantes corpúsculos es el ejemplo más sencillo de una acción próxima; pues la acción del primer punto sobre el último es transmitida por las masas intermedias y no se verifica al instante, sino con un retraso. La fuerza ejercida por una partícula sobre la inmediata vecina queda, sin embargo, concebida como acción a distancia, aunque es corta la tal distancia; pero cabe representarse las distancias entre las partículas tan pequeñas como se quiera, aumentando su número en proporción, aunque de suerte que la masa total siga siendo la misma. Y entonces la cadena de partículas con masa se transforma en el concepto límite de un continuo material; las fuerzas actúan entre partículas infinitamente próximas y las leyes del movimiento toman la forma de ecuaciones diferenciales. Son éstas la expresión matemática del concepto físico de la acción próxima.

Vamos a seguir ese proceso límite en las leyes de movimiento de nuestra cadena de partículas,

fig65

Consideremos desplazamientos puramente transversales (figura 65). En la teoría de la elasticidad admítese que una partícula P es desplazada por su vecina Q con tanta mayor fuerza cuanto que está más alejada transversalmente con respecto a Q. Sea u el exceso del desplazamiento transversal de P sobre el de Q; sea a la primitiva distancia de las partículas en la recta. Deberá ser la fuerza retroactiva proporcional a la relación ${\tfrac {u}{a}}=d$, que se llama deformación. Establecemos:

$K=p\cdot {\frac {u}{a}}=pd$;

donde p es un número constante, que es manifiestamente igual a la fuerza, cuando la deformación d=1. Se designa p con el nombre de constante de elasticidad.

La misma partícula de su otra vecina R experimenta igualmente una fuerza $K'=p{\tfrac {u'}{a}}=pd'$. Pero, salvo en el caso singular de que la oscilación de P sea justamente un máximum, la partícula R será desplazada más fuertemente que P y, por tanto, no tratará de retrotraer ésta sino de aumentar su desplazamiento. K' actuará, pues, contrariamente a K.

La fuerza resultante sobre la partícula P es la diferencia de esas fuerzas:

$K-K'=p(d-d')$.

Esta determina, pues, el movimiento de P según la fórmula dinámica fundamental de que la masa por la aceleración es igual a la fuerza:

$mb=K-K'=p(d-d')$.

Ahora bien; pensemos el número de las partículas aumentado sin cesar y sus masas disminuidas en igual razón, de suerte que la masa por unidad de longitud conserve siempre el mismo valor. Si en la unidad de longitud entran n partículas, tendremos n·a = 1; es decir, $n={\tfrac {1}{a}}$. La masa por unidad de longitud es $mn={\tfrac {m}{a}}$; se llama a esta magnitud la densidad de masas (lineal) y se designa con ρ. Dividiendo ahora la ecuación anterior por a, obtiénese:

${\frac {m}{a}}b=\rho b={\frac {K-K'}{a}}=p{\frac {d-d'}{a}}$,

y aquí estamos ante formas completamente semejantes a las que vimos en la definición de los conceptos de velocidad y aceleración. Así, en efecto, como la velocidad era la relación entre el camino x y el tiempo t, $v={\tfrac {x}{t}}$, en la cual, para un movimiento acelerado, hay que pensar el tiempo t como brevísimo, de igual modo tenemos aquí la deformación $d={\tfrac {u}{a}}$, que es la relación entre el desplazamiento relativo y la distancia primitiva, la cual hay que pensarla como extraordinariamente pequeña. Del mismo modo que la aceleración fué definida como variación de la velocidad en relación con el tiempo,

$b={\frac {w}{t}}={\frac {v-v'}{t}}$,

de igual manera obtenemos aquí la magnitud

$f={\frac {d-d'}{a}}$,

que, por modo análogo, mide la variación de la deformación de punto a punto.

Así como la velocidad v y la aceleración b conservan su sentido y valor finito para períodos de tiempo decrecientes cuanto se quiera, así también las cantidades d y f conservan su sentido y valor finito para distancias a que decrecen cuanto se quiera; todos éstos son los llamados cocientes diferenciales, y tanto $v={\tfrac {x}{t}}$ como $d={\tfrac {u}{a}}$ son de primer orden, mientras que $b={\tfrac {v-v'}{t}}$ como $f={\tfrac {d-d'}{a}}$ son de segundo orden.

La ecuación del movimiento es, pues, una ecuación diferencial de segundo orden:

$\rho b=pf$,[32]

y tanto con respecto a la variación del proceso en el tiempo como en el lugar. De este tipo son todas las leyes de acción próxima en la física teórica. Si se trata, por ejemplo, de cuerpos elásticos extensos en todas las direcciones, añádense, para las otras dos dimensiones del espacio, otros miembros construidos por modo análogo. Pero también en la teoría de los procesos eléctricos y magnéticos rigen leyes muy semejantes; por último, la teoría de la gravitación ha sido reducida por Einstein a una forma como ésta.

Debemos advertir aún que leyes de acción a distancia pueden escribirse en la forma de fórmulas de acción próxima. Por ejemplo, si en nuestra ecuación [32] suprimimos el miembro ρb, es como si admitiéramos que la densidad de masas se hace infinitamente pequeña, y entonces un desplazamiento de la primera partícula producirá al momento una fuerza sobre la última partícula, porque la inercia de los miembros intermedios ha desaparecido. Tendremos propiamente la propagación de una fuerza con velocidad infinita, una verdadera acción a distancia. Y, sin embargo, la ley pf = 0 aparece en la forma de una ecuación diferencial, de una acción próxima. En la teoría de la electricidad y del magnetismo encontraremos algunas de estas pseudoleyes de acción próxima; en esas teorías es justamente donde esas leyes han abierto el camino a las verdaderas leyes de acción próxima. Lo esencial en éstas es el miembro que representa la inercia, que es el que hace que la propagación de perturbaciones en el equilibrio tenga una velocidad finita y, por tanto, produce las ondas.

En la ley [32] aparecen dos cantidades que determinan el carácter físico de la substancia: la masa por unidad de volumen o densidad ρ y la constante de elasticidad p. Si se escribe $b={\tfrac {p}{\rho }}f$ se ve que, en una deformación dada, esto es, dada f la aceleración es tanto mayor cuanto mayor es p y menor es ρ pero p es justamente una medida de la rigidez elástica de la substancia, y ρ mide la inercia de las masas, y es claro que un aumento de rigidez acelera el movimiento y que un aumento de inercia lo alenta. La velocidad c de una onda dependerá, pues, solamente de la relación ${\tfrac {p}{\rho }}$, pues cuanto más de prisa corra la onda, tanto mayores son las aceleraciones de las partículas singulares de la substancia. La ley exacta de esta conexión se encuentra por la reflexión siguiente:

Un punto de masa verifica un movimiento periódico sencillo de la especie que anteriormente hemos investigado (II, 11, página 49). Allí hemos demostrado que la aceleración está en conexión con la oscilación x, según la fórmula [8]:

$b=(2\pi \nu )^{2}x$,

siendo ν el número de oscilaciones por segundo; si se pone en lugar de éste la duración de la oscilación, según la fórmula [30], $T={\tfrac {1}{\nu }}$, tendremos:

$b=({\frac {2\pi }{T}})^{2}x$.

La misma reflexión que hemos hecho aquí para la sucesión en el tiempo puede aplicarse a la yuxtaposición en el espacio, y se llegará a relaciones correspondientes; no hay mas que substituir la aceleración b (el cociente diferencial segundo, temporal) por la cantidad f (cociente diferencial segundo, de lugar) y la duración de oscilación T (el periodo de tiempo) por la longitud de onda λ (período de lugar). Así llegamos a la fórmula

$f=({\frac {2\pi }{\lambda }})^{2}x$.

Si las dos expresiones de b y de f se dividen una por otra, se eliminará el factor (2π)²x y quedará:

${\frac {b}{f}}={\frac {\lambda ^{2}}{T^{2}}}$.

Ahora bien; por una parte, según la fórmula [31] (pág. 115), es ${\tfrac {\lambda }{T}}=c$ y, por otra parte, según [32] (pág. 130), es ${\tfrac {b}{f}}={\tfrac {p}{\rho }}$; de donde sigue que

$c^{2}={\frac {p}{\rho }}$, o sea $c={\sqrt {\frac {p}{\rho }}}$[33]

En un cuerpo que se extiende en las tres direcciones del espacio pueden, empero, propagarse tres ondas en cada dirección, con diferentes velocidades, una longitudinal y dos transversales; esto es porque, para las condensaciones y dilataciones de las ondas longitudinales, es determinante otra constante de elasticidad p que para los laterales desplazamientos de las vibraciones transversales. En los cuerpos no cristalinos, las dos ondas transversales tienen direcciones distintas de vibración, que son perpendiculares una a otra, pero la misma velocidad c₁; la onda longitudinal tiene otra velocidad c₂ (fig. 66).

fig66

Todos estos hechos se confirman por experimentos en ondas sonoras sobre cuerpos sólidos.

Volvamos ahora al punto de partida de estas consideraciones, esto es, a la teoría elástica de la luz.

Esta consiste en identificar el éter portador de las vibraciones luminosas con un cuerpo sólido elástico; las ondas luminosas son entonces en cierto modo ondas sonoras en ese medio hipotético.

¿Qué propiedades deben atribuirse a ese éter elástico?

Ante todo, la enorme velocidad de propagación c exige, o que sea muy grande la rigidez elástica p, o que sea muy pequeña la densidad de masa ρ, o las dos cosas a la vez. Pero como la velocidad de la luz es distinta en diferentes substancias, deberá el éter, dentro de un cuerpo material, o estar condensado o variar de elasticidad, o ambas cosas a la vez. Se ve que aquí se ofrecen distintos caminos. Y el número de las posibilidades aumenta por el hecho de que, como hemos visto, no cabe decidir experimentalmente si las vibraciones de la luz polarizada se verifican paralela o perpendicularmente al plano de polarización (plano de incidencia del espejo polarizador).

En correspondencia con esta indeterminación del problema, encontramos históricamente un gran número de teorías diferentes del éter elástico. Ya hemos citado los nombres de los autores mas importantes; junto a los matemáticos franceses Poisson, Fresnel, Cauchy y el inglés Green aparece por vez primera un físico alemán importante, Franz Neumann, el maestro de la gran generación de los físicos alemanes Helmholtz, Kirchhoff, Clausius.

Hoy nos admira la agudeza y la paciencia que se ha gastado en el problema de concebir los fenómenos ópticos en su totalidad como movimientos de un éter elástico, con las mismas propiedades que tienen los cuerpos sólidos elásticos materiales. Nos parece una exageración del principio que dice: explicar es reducir lo desconocido a lo conocido. Pues hoy sabemos que la esencia del cuerpo sólido elástico no es cosa sencilla, ni mucho menos conocida; la física del éter se ha manifestado más sencilla y transparente que la física de la materia, y la investigación moderna se afana por reducir la constitución de la materia, como fenómeno secundario, a las propiedades de los campos de fuerza, que han sobrevivido al éter de la física pretérita. Pero esta variación del programa científico se debe en no pequeña parte a los fracasos que hubieron de sufrir los ensayos de componer una teoría consecuente del éter elástico.

Una objeción que parece importante contra esta teoría es que un éter que llenase el espacio cósmico, una substancia de la gran rigidez que debe tener para ser sustentáculo de las rápidas vibraciones luminosas, tendría que oponer una resistencia al movimiento de los astros, sobre todo de los planetas. Mas la astronomía nunca ha encontrado desviaciones de las leyes de Newton que pudieran indicar semejante resistencia. Stokes (1845) ha quitado en cierto modo mucha fuerza a esta objeción, observando que el concepto de solidez de un cuerpo es algo totalmente relativo y depende del curso temporal de las fuerzas deformadoras. Un trozo de pez—el lacre y el vidrio se conducen lo mismo—salta a un martillazo en pedazos lisos y agudos; pero si se carga sobre él un peso, éste se hunde, aunque lentamente, poco a poco en la pez, como si ésta fuese un líquido viscoso. Ahora bien; las fuerzas que se presentan en las vibraciones luminosas y que cambian con extraordinaria rapidez (600 billones de veces por segundo) están, con respecto a los procesos relativamente lentos de los movimientos planetarios en su curso temporal, en una relación mucho más extrema que el martillazo con respecto al peso depositado sobre la pez. Por eso puede funcionar el éter para la luz como cuerpo sólido elástico y, en cambio, ser por completo dócil al movimiento de los planetas.

Pero aun cuando se quiera hallar satisfacción con este espacio cósmico lleno de pez, surgen serias dificultades de las leyes mismas de la propagación de la luz. Sobre todo, en los cuerpos sólidos elásticos preséntase siempre, además de las dos ondas transversales, una onda longitudinal; si se sigue la refracción de una onda en el límite de dos medios y se admite que la onda en el primer medio vibra transversalmente, entonces en el segundo medio surge necesariamente al mismo tiempo una vibración longitudinal. Han fracasado todos los intentos de evitar esa consecuencia de la teoría por medio de variaciones más o menos caprichosas. Se llegó incluso a hipótesis tan singulares como la de que el éter ofrece a la compresión una resistencia infinitamente pequeña o infinitamente grande, comparada con la rigidez frente al desplazamiento transversal; en el primer caso, las ondas longitudinales serían infinitamente lentas; en el segundo, infinitamente rápidas; pero en ningún caso se manifestarían en forma de luz. Un físico, Mac Cullagh (1839), llegó hasta el punto de construir un éter que se separaba por completo del modelo de los cuerpos elásticos; en efecto, mientras éstos oponen resistencia a toda variación de distancia entre sus partículas, pero siguen sin resistencia las meras rotaciones, el éter de Mac Cullagh, en cambio, se conduce inversamente. No podemos detenernos más en esta teoría; por extraña que parezca, es, sin embargo, muy significativa como predecesora de la teoría electromagnética de la luz. Conduce casi a las mismas fórmulas que ésta, y está, efectivamente, en disposición de exponer los procesos ópticos con bastante amplitud. Es claro que, por medio de contrucciones caprichosas, cabe encontrar modelos de éter en los cuales puede exponerse una determinada esfera de fenómenos; pero estas invenciones no reciben un valor de conocimiento, hasta que conducen a fusionar dos terrenos de la física que hayan permanecido aislados hasta entonces. En esto está el gran progreso que Maxwell ha realizado coordinando la óptica en la serie de los fenómenos electromagnéticos.

7. La óptica de los cuerpos en movimiento.

Antes de proseguir esta evolución, vamos a hacer un alto y plantear el problema de cómo la teoría del éter elástico se relaciona con el problema del espacio-tiempo y con la relatividad. Hasta ahora, en las investigaciones ópticas no hemos considerado los movimientos de los cuerpos que emiten, reciben y dejan pasar la luz; ahora vamos a considerar justamente esos movimientos.

El espacio de la mecánica es considerado como vacío, dondequiera que no haya cuerpos materiales; el espacio de la óptica está lleno del éter. Pero el éter tiene aquí el sentido de una especie de materia a la cual corresponde una determinada densidad de masa y una elasticidad. Se puede, por tanto, trasladar la mecánica de Newton, con su teoría del espacio y el tiempo, al universo lleno de éter. Este universo no consiste ya en masas separadas por espacios vacíos, sino que está enteramente lleno por la masa sutil del éter, en la cual flotan las masas más groseras de la materia; el éter y la materia actúan uno sobre otra con fuerzas mecánicas y se mueven según las leyes de Newton. El punto de vista de Newton es, pues, idealmente aplicable a la óptica; se trata de saber tan sólo si las observaciones concuerdan con ello.

Pero esta cuestión no puede decidirse sencillamente por medio de experimentos unívocos; pues el estado de movimiento del éter fuera y dentro de la materia no es conocido y hay libertad de inventar hipótesis acerca de él. Debe, pues, plantearse la cuestión así: ¿es posible hacer tales suposiciones acerca de la acción reciproca de los movimientos del éter y de la materia, que por ellas se expliquen en su totalidad los fenómenos ópticos?

Recordemos ahora la teoría del principio clásico de la relatividad. Según él, el espacio absoluto no existe sino en sentido limitado; pues todos los sistemas inerciales que se mueven, unos respecto de otros, con movimiento rectilíneo uniforme pueden considerarse con igual derecho como inmóviles en el espacio. La primer hipótesis sobre el éter luminoso que se presenta será, pues:

El éter en el espacio cósmico, fuera de los cuerpos materiales, está inmóvil en un sistema inercial.

Si así no fuera, habría partes del éter aceleradas; manifestaríanse entonces en él fuerzas centrifugas y, como consecuencia de ellas, variaciones de densidad y elasticidad, y debería esperarse que la luz de los astros nos diera conocimiento de ello.

Esta hipótesis satisface, por la forma, el principio clásico de la relatividad; si el éter se considera como cuerpo material, entonces los movimientos de traslación que los cuerpos verifiquen con respecto al éter son movimientos relativos, como los de dos cuerpos uno con respecto del otro, y un movimiento común de traslación del éter y de toda materia no seria apreciable ni mecánica ni ópticamente.

Pero la física de los cuerpos materiales solos, sin el éter, ya no necesita satisfacer al principio de relatividad; una traslación común de la materia toda, sin que en ella tome parte el éter, es decir, un movimiento relativo al éter, podría muy bien comprobarse por medio de experimentos ópticos. En tal caso, el éter definiría, prácticamente, un sistema de referencia absoluto. La cuestión que interesa en lo que ha de seguir es la de si los fenómenos ópticos observables dependen sólo de los movimientos relativos de los cuerpos materiales, o si el movimiento en el mar del éter puede observarse.

Una onda luminosa se caracteriza por tres notas:

1.ª El número de vibraciones o frecuencia.

2.ª La velocidad.

3.ª Le dirección de propagación. Investigaremos si temáticamente el influjo que sobre esos tres caracteres de la onda luminosa tienen los movimientos relativos de los cuerpos que emiten luz y los que la reciben, unos con respecto a los otros y con respecto al medio en que se propaga, ya sea el éter en el espacio cósmico, ya sea una substancia transparente.

fig67

El método empleado es el siguiente: consideramos un tren de ondas que en el tiempo t = 0 abandona el punto cero en una dirección y contamos las ondas individuales que pasan por un punto P cualquiera, en el tiempo t. Este número evidentemente es independiente del sistema de referencia en que se midan las coordenadas de P; el sistema puede estar inmóvil o en movimiento. Determínase ese número del modo siguiente:

La primera onda que sale del punto-cero en el momento t = 0 tiene que recorrer cierta distancia s (fig. 67) antes de alcanzar el punto P; para ello necesita el tiempo ${\tfrac {s}{c}}$. A partir de este momento, contemos las ondas que pasan por P hasta el momento t; esto es, durante el tiempo $t-{\tfrac {s}{c}}$. Ahora bien; la luz, en un segundo, verifica ν vibraciones, y a cada onda que pasa corresponde, exactamente, una vibración; por tanto, en un segundo pasan ν ondas, esto es, en $t-{\tfrac {s}{c}}$sec, pasarán $\nu (t-{\frac {s}{c}})$ ondas por el punto P.

El número de ondas $\nu (t-{\frac {s}{c}})$ depende, pues, tan sólo de la posición de los puntos cero y P, respectivamente, y respecto del tren de ondas, y del valor del tiempo t que haya de transcurrir entre la salida de la primera onda en O y la llegada de la última a P. Este número no tiene nada que ver con el sistema de referencia; es, pues, un invariante en el sentido que ya hemos dado a esta palabra.

La mejor manera de comprender esto claramente es hacer uso de las expresiones de Minkowski. Según éstas, la salida de la onda primera, en el tiempo t = 0, del punto cero es un suceso, un punto universal; la llegada de la última onda en el t al punto P es otro suceso, un segundo punto universal. Pero los puntos universales existen sin referencia a un determinado sistema de coordenadas; y como el número de ondas $\nu (t-{\tfrac {s}{c}})$ está determinado solamente por los dos puntos universales, es independiente del sistema de referencia, es invariante.

De aquí se siguen fácilmente, o por medio de reflexiones intuitivas o por aplicación de las transformaciones de Galileo, todas las leyes que presiden a la conducta de las tres notas de las ondas, frecuencia, dirección y velocidad, al verificarse un cambio de sistema de referencia.

Deduciremos esas leyes según su orden y las compararemos con la experiencia.

8. El efecto de Doppler.

Christian Doppler (1842) ha descubierto que la frecuencia observada de una onda depende del movimiento, tanto del foco luminoso como del observador, respectivamente al medio donde se propaga. Es fácil observar el fenómeno en las ondas sonoras; el pitido de una locomotora parece más alto cuando se acerca al observador, y se torna más profundo en el momento de pasar ante él. El foco sonoro, al acercarse, lleva las impulsiones hacia adelante, de suerte que éstas se siguen con mayor rapidez. Un efecto semejante produce el movimiento del observador hacia el foco de sonido; el observador recibe las ondas en sucesión más rápida. Lo mismo debe de suceder con la luz. Pero la frecuencia de la luz es la que determina su color, y las vibraciones más rápidas corresponden al violeta, las más lentos al rojo; términos ambos del espectro. Por tanto, si se acercan el foco luminoso y el observador, el color de la luz se correrá un poco hacia el violeta, y si se alejan, se correrá hacia el rojo.

Este fenómeno ha sido, efectivamente, observado.

La luz procedente de gases luminosos no consiste en todas las vibraciones posibles, sino en cierto número de frecuencias separadas; el espectro que produce un prisma o un aparato espectral fundado en interferencia no presenta una cinta continua de colores, como el arco iris, sino lineas aisladas, precisas y matizadas. La frecuencia de estas líneas espectrales es característica de los elementos químicos que brillan en la llama (análisis espectral de Bunsen y Kirchhoff, 1859). También los astros tienen esos espectros lineares, cuyas líneas, en su mayor parte, coinciden con las de elementos terrestres; de donde se concluye que la materia en los más lejanos espacios cósmicos está compuesta de los mismos elementos que en la tierra. Pero las líneas de las estrellas no coinciden exactamente con las correspondientes de la Tierra, sino que presentan pequeños desplazamientos en un sentido durante medio año, y en el sentido opuesto durante el otro medio año. Estas variaciones de la frecuencia son resultados del efecto de Doppler, por causa del movimiento de la Tierra alrededor del Sol; durante medio año corre la Tierra al encuentro de determinada estrella fija, por lo cual aumenta la frecuencia de todas las ondas luminosas que de ésta vienen, y las líneas espectrales de la estrella aparecen corridas hacia el lado de las vibraciones más rápidas (violeta); durante el otro medio año aléjase la Tierra de la estrella, y el corrimiento de las líneas espectrales se verifica hacia el otro lado (rojo).

Esta admirable reproducción del movimiento de la Tierra en el espectro de las estrellas no aparece, desde luego, pura en el fenómeno; pues es bien claro que sobre ella se superpone el efecto de Doppler, producido por el envío de luz desde un foco luminoso en movimiento. Si las estrellas fijas no están todas inmóviles en el éter, tendrá su movimiento que darse a conocer como corrimiento de las líneas espectrales; éste se añadirá al producido por el movimiento de la Tierra; pero como no presenta el cambio anual, puede separarse de él. Astronómicamente, es este fenómeno aun mucho más importante, pues da conocimiento de las velocidades de las más lejanas estrellas, en cuanto que éstas, al moverse, se alejen o se acerquen a la Tierra. Pero no es nuestro objeto seguir estas investigaciones en detalle.

Nos interesa ante todo la cuestión siguiente:

¿Qué sucede cuando el observador y el foco luminoso se mueven en la misma dirección y con igual velocidad? ¿Desaparece entonces el efecto de Doppler? ¿Depende tan sólo del movimiento relativo de los cuerpos materiales, o no desaparece, y delata en esto el movimiento de los cuerpos por el éter? En el primer caso quedaría cumplido el principio de relatividad para los procesos ópticos entre cuerpos materiales.

La teoría del éter da a estas preguntas la respuesta siguiente:

El efecto de Doppler no depende sólo del movimiento relativo del foco luminoso y del observador, sino también un poco de los movimientos de ambos con respecto al éter; pero este influjo es tan pequeño, que escapa a la observación y, además, es estrictamente igual a cero en el caso de una traslación común del foco luminoso y del observador.

Esto último es tan claro intuitivamente, que apenas necesita subrayarse; basta reflexionar que las ondas pasan con el mismo ritmo por dos puntos cualesquiera que estén inmóviles uno con respecto al otro, siendo indiferente que los dos puntos estén inmóviles en el éter o se muevan en común. Sin embargo, el principio de relatividad no vale estrictamente para los cuerpos que envían luz y reciben luz, sino sólo aproximadamente. Vamos a demostrarlo.

Para ello emplearemos la ley antes deducida, que dice que el número de ondas es invariante.

Desde el punto cero del sistema S, inmóvil en el éter, hacemos partir un tren de ondas en la dirección x, y contamos las ondas que pasan por un punto cualquiera P durante el tiempo t (figura 68). El camino que las ondas han de recorrer es igual a la coordenada x del punto P; hay que poner, pues, s = x, y el número de ondas vale:

fig68

$\nu (t-{\frac {x}{c}})$

Ahora bien; consideremos un sistema S', que se mueve en la dirección x, con la velocidad v, y en este sistema un observador inmóvil en un lugar que tiene la coordenada x'; en el tiempo t = 0 coincidirán S y S', y en el tiempo t el observador alcanzará el punto P. Entonces el mismo número de ondas es, en el sistema S', igual a

$\nu '(t-{\frac {x'}{c'}})$;

siendo ν' y c' la frecuencia y la velocidad medidas por el observador en movimiento. Vale, pues, la fórmula

$\nu (t-{\frac {x}{c}})=\nu '(t-{\frac {x'}{c'}})$[34]

en la cual se conexionan las coordenadas por la transformación de Galileo [25]:

$x'=x-vt$ ó $x=x'+vt$

Substitúyase este valor, y se obtiene:

$\nu (t-{\frac {x'+vt}{c}})=\nu '(t-{\frac {x'}{c'}})$,[35]

que debe regir, naturalmente, para todos los valores de x' y t. Si se elige especialmente t = 1, x' = 0, se deriva:

$\nu (1-{\frac {v}{c}})=\nu '$[36]

Esta es la ley que buscábamos; expresa que un observador que se mueve en la misma dirección que las ondas luminosas mide una frecuencia ν' que está empequeñecida en la relación

$(1-{\frac {v}{c}}):1$

Consideremos ahora inversamente un foco luminoso que vibra con la frecuencia ν₀ y se mueve, en la dirección del eje x, con la velocidad v₀; un observador inmóvil en el éter medirá la frecuencia ν. Este caso es en seguida reductible al anterior; pues foco de luz u observador, ello es indiferente para la consideración; lo que importa es el ritmo con que las ondas pasen por un punto. Ahora el punto en movimiento es el foco luminoso; obtenemos, pues, la fórmula para este caso sacándola de la anterior, poniendo, en vez de v, v₀, y en vez de ν', ν₀:

$\nu (1-{\frac {v_{0}}{c}})=\nu _{0}$

pero ν₀ es dado aquí como frecuencia del foco luminoso, y ν es buscado como frecuencia observada. Se obtiene, pues:

$\nu ={\frac {\nu _{0}}{1-{\frac {v_{o}}{c}}}}$[37]

La frecuencia observada, pues, puesto que el denominador es más pequeño que 1, aparecerá aumentada en la proporción

$1:(1-{\frac {v_{0}}{c}})$

Se ve al punto que no es indiferente que el observador se mueva en una dirección o el foco luminoso en dirección opuesta, con la misma velocidad. Pues si en la fórmula [37] se pone $v_{0}=-v$, se transformará en

$\nu ={\frac {\nu _{0}}{1+{\frac {v}{c}}}}$

y esta fórmula es distinta de la [36]. Desde luego es la diferencia pequeñísima en todos los casos prácticos. Ya hemos visto antes que la relación de la velocidad de la Tierra en su trayectoria en torno al Sol con la velocidad de la luz es $\beta ={\tfrac {v}{c}}=1:10000$ y semejantes pequeños valores de β rigen para todos los movimientos cósmicos. Entonces, con gran aproximación, puede decirse que

${\frac {1}{1+\beta }}=1-\beta$

pues si se desprecia $\beta ^{2}={\tfrac {1}{100000000}}=10^{-8}$, comparado con 1, se halla que $(1+\beta )(1-\beta )=1-\beta ^{2}=1$.

Este desprecio del cuadrado de $\beta ={\tfrac {v}{c}}$ tendrá en lo que sigue un papel importante. Es casi siempre permitido, porque cantidades tan pequeñas como $\beta ^{2}=10^{-8}$ no son accesibles a la observación sino en muy pocos casos. Ahora bien; clasifícanse en general los fenómenos de la óptica (y electrodinámica) de cuerpos en movimiento, dividiéndolos en cantidades del orden β o del orden β², y a las primeras se les llama cantidades de primer orden, y a las segundas, cantidades de segundo orden con respecto a β.

En este sentido podemos decir:

El efecto de Doppler depende sólo del movimiento relativo del foco luminoso y del observador, cuando se desprecian cantidades del segundo orden.

Ello se ve también cuando se admite un movimiento simultáneo del foco luminoso (velocidad v₀) y del observador (velocidad v) entonces se obtiene la frecuencia observada ν', poniendo ν de la fórmula [37] en la [36]:

$\nu '=\nu (1-{\frac {v}{c}})=\nu _{0}{\frac {1-{\tfrac {v}{c}}}{1-{\tfrac {v_{0}}{c}}}}$.

Si el foco luminoso y el observador tienen la misma velocidad v₀ = v, resuélvese el quebrado y se obtiene ν' = ν₀; el observador nada nota de un movimiento común con el foco luminoso respecto del éter. Pero tan pronto como v es diferente de v₀, surge un efecto de Doppler cuya cantidad no depende sólo de la diferencia de velocidades v-v₀; de esa suerte podría determinarse el movimiento con respecto al éter, si la diferencia no fuere de segundo orden, esto es, demasiado pequeña para ser observada.

Vemos, pues, que el efecto de Doppler no es un medio prácticamente útil para comprobar movimientos con respecto al éter en el espacio cósmico.

fig69

Hemos de añadir aún que se ha conseguido hallar el efecto de Doppler con focos luminosos terrestres. Para ello hay que disponer de focos luminosos que se muevan con rapidez extraordinaria, para que la relación $\beta ={\tfrac {v}{c}}$ reciba un valor notable. J. Stark (1906) usó los llamados rayos canales. Si en un tubo donde se ha hecho el vacío, y que se ha llenado de hidrógeno fuertemente enrarecido, se llevan dos electrodos, uno de los cuales está agujereado, y se hace de éste el polo negativo (cátodo) de una descarga eléctrica (fig. 69), prodúcense primero los conocidos rayos catódicos; pero luego corre por los canales del cátodo, como Goldstein (1886) ha descubierto, un resplandor rojizo que procede de los átomos o moléculas de hidrógeno, que, cargadas positivamente, se mueven con rapidez. La velocidad de esos rayos canales es del orden $v=10^{8}$ cm. por segundo; tiene, pues, β la cantidad:

$\beta ={\frac {10^{8}}{3\cdot 10^{10}}}={\frac {l}{300}}$

que es considerable comparada con las cantidades astronómicas.

Stark investigó el espectro de los rayos canales y halló que las líneas claras del hidrógeno muestran el desplazamiento que era de esperar, fundado en el efecto de Doppler. Este descubrimiento tiene una gran importancia para la atomística física; sin embargo, esto no pertenece a nuestro tema.

Por último, hemos de mencionar que Belopolski (1895) y Galizin (1907) han demostrado una especie de efecto de Doppler por medio de focos luminosos terrestres y espejos en movimiento.

9. La conducción de la luz por la materia.

Llegamos ahora a la investigación del segundo carácter de una onda luminosa, a saber, su velocidad. Según la teoría del éter, es la velocidad de la luz una cantidad determinada por la densidad de masa y la elasticidad del éter; tiene, pues, un valor fijo en el éter del espacio cósmico, un valor diferente en cada cuerpo material, y este valor dependerá del modo como la materia influya en el interior del éter y lo lleve consigo en su movimiento.

Consideremos primero la velocidad de la luz en el espacio cósmico; debemos concluir que un observador en movimiento con respecto al éter medirá otra velocidad que un observador inmóvil; pues aquí valen manifiestamente las leyes elementales del movimiento relativo. Si el observador se mueve en la misma dirección que la luz, la velocidad de ésta quedará disminuida de la cantidad de velocidad v del observador con respecto al éter; es más: podrían fingirse seres que fuesen más veloces que la luz. Otro tanto ofrecen las fórmulas deducidas más arriba, que expresan las relaciones generales entre las propiedades de la luz, cuando las establecen dos observadores que se encuentran en traslación relativa. Si en la fórmula [35] se pone t = 0, x' = 1, se obtiene

${\frac {\nu }{c}}={\frac {\nu '}{c'}}$,

y si aquí se pone la expresión de ν' por la fórmula [36]

${\frac {\nu }{c}}={\frac {\nu '}{c}}(1-{\frac {v}{c}})$,

o, puesto que ν se elimina,

$c'=c(1-{\frac {v}{c}})=c-v$.[38]

Esto significa que la velocidad de la luz en el sistema en movimiento se determina según las reglas del movimiento relativo.

Esto puede también concebirse de manera que un observador en movimiento a través del éter está acariciado por un viento de éter, que disipa las ondas luminosas, como en un automóvil a gran velocidad el viento pasa barriéndolo y se lleva consigo el sonido.

Con esto, empero, está sólo dado un medio para determinar el movimiento, por ejemplo, de la Tierra o del sistema solar con respecto al éter. Tenemos dos métodos, esencialmente distintos, de medir la velocidad de la luz, uno astronómico y otro terrestre; el primero, el antiguo proceder de Römer, emplea los eclipses de los satélites de Júpiter; mide, pues, la velocidad de la luz que viene de Júpiter a la Tierra por el espacio cósmico; en el otro método, el foco luminoso y el observador toman ambos parte en el movimiento de la Tierra. Ahora bien; ¿dan ambos métodos exactamente el mismo resultado, o preséntanse diferencias que delatan un movimiento con respecto al éter cósmico?

fig70

Maxvell (1879) ha hecho notar que por medio de la observación de los eclipses de los satélites de Júpiter tenía que determinarse un movimiento de todo el sistema solar con respecto al éter cósmico. Representémonos al planeta Júpiter en un punto cualquiera A (fig. 70) de su trayectoria. Durante un año aléjase poco de A, pues su tiempo de revolución es de doce años. En un año recorre la Tierra una vez su trayectoria, y por observación de los eclipses se puede encontrar el tiempo que la luz necesita para recorrer el diámetro de la trayectoria terrestre. Si ahora el sistema solar entero se mueve en la dirección que va del Sol a A, entonces la luz que de Júpiter viene a la Tierra camina al encuentro de ese movimiento y su velocidad aparecerá agrandada. Ahora bien; espérense seis años a que Júpiter se halle en el punto opuesto B de su trayectoria; ahora la luz corre en la misma dirección que el sistema solar y necesita más tiempo para pasar a la trayectoria terrestre; su velocidad aparecerá menor.

Cuando Júpiter se encuentra en A, los eclipses de uno de sus satélites tienen que aparecer alterados por el valor de tiempo $t_{1}={\tfrac {l}{c+v}}$siendo l el diámetro de la trayectoria terrestre; cuando Júpiter está en B, vale la alteración $t_{2}={\tfrac {l}{c-v}}$. Si el sistema solar estuviese inmóvil en el éter serían iguales ambas alteraciones, a saber: $t_{0}){\tfrac {l}{c}}$; su diferencia efectiva es

$t_{2}-t_{1}=l({\frac {1}{c-v}}-{\frac {1}{c+v}}={\frac {2lv}{c^{2}-v^{2}}}={\frac {2lv}{c^{2}(1-\beta ^{2})}}$

para lo cual, despreciando β², puede escribirse:

$t_{2}-t_{1}={\frac {2lv}{c^{2}}}=2t_{0}\beta$,

que permite una determinación de β y, por tanto, de la velocidad v=βc del sistema solar con respecto al éter. Ahora bien; la luz, para venir del Sol a la Tierra, necesita unos 8 minutos; es, pues, t₀ = 16 minutos, o, en cifras redondas, t₀ = 1000 sec. Habría que concluir, pues, una diferencia de tiempo

$t_{2}-t_{1}=1$sec. por $\beta ={\frac {1}{2000}}$

o sea

$v=\beta c={\frac {300000}{2000}}=150$km./sec.

Las velocidades relativas de las estrellas fijas respecto del sistema solar, velocidades que se pueden derivar por el efecto de Doppler, hállanse, en su mayor parte, en el orden de magnitud 20 km./sec; pero para ciertas aglomeraciones de estrellas y nieblas espirales preséntanse velocidades hasta de 300 kilómetros/sec. La exactitud de las determinaciones astronómicas de tiempo no ha conseguido hasta ahora comprobar una alteración de los eclipses de un satélite de Júpiter, que valga 1 sec., o menos, durante medio año; pero no puede decirse que no lo consiga algún día por refinamiento de los medios de observación.

También un observador que se hallase en el Sol, y para quien fuera conocido el valor de la velocidad de la luz en el éter, podría determinar el movimiento del sistema solar por entre el éter, merced a los eclipses de los satélites de Júpiter; necesitaría para ello medir la alteración de los eclipses durante medio curso de la trayectoria de Júpiter. Para ello vale la misma fórmula $t_{2}-t_{1}=2t_{0}\beta$; sino que ahora t₀ significa el tiempo que la luz necesita para recorrer el radio de la trayectoria de Júpiter. Ese valor t₀ es (unas 2,5 veces) mayor que el arriba usado de diez y seis minutos para la trayectoria de la Tierra, y en igual proporción será mayor la alteración t₂ - t₁; pero, en cambio, la duración de la revolución de Júpiter, durante la cual tienen que seguirse sucesivamente los eclipses, es mucho mayor (unas doce veces) que el año terrestre; de suerte que ese método, que también podría usar un observador terrestre, no parece prometer ninguna ventaja.

En todo caso, el hecho de que, con la exactitud hoy asequible de algunos segundos, no se ha encontrado alteración ninguna, es prueba de que la velocidad del sistema solar con respecto al éter no es mucho mayor que las mayores velocidades relativas conocidas de los astros unos con respecto a otros.

Veamos ahora los métodos terrestres para medir la velocidad de la luz. Aquí es fácil comprender por qué estos métodos no permiten conclusiones acerca del movimiento de la Tierra a través del éter; ya indicamos la causa más arriba, cuando mencionamos por vez primera estos métodos (pág. 112). En estos métodos recorre la luz uno y el mismo camino de ida y vuelta; lo que se mide es una velocidad media en ese viaje de ida y vuelta; esta velocidad difiere de la velocidad de la luz, c, en el éter, por sólo una cantidad de segundo orden respectivamente a β, y escapa a la observación. Sea, en efecto, l la longitud del camino; entonces el tiempo que la luz emplea para recorrerlo en el sentido del movimiento de la Tierra será igual a ${\tfrac {l}{c-v}}$; el tiempo para la vuelta será ${\tfrac {l}{c+v}}$, y el tiempo total será:

$l({\frac {1}{c+v}}+{\frac {1}{c-v}})={\frac {2lc}{(c+v)(c-v)}}={\frac {2lc}{c^{2}-v^{2}}}$.

La velocidad media es 2l dividido por este tiempo total; esto es:

${\frac {c^{2}-v^{2}}{c}}=c(1-{\frac {v^{2}}{c^{2}}})$

y se distingue de c solamente por cantidades de segundo orden.

Además de la medición directa de la velocidad de la luz, hay muchos otros experimentos en que la velocidad de la luz entra en juego. Todos los fenómenos de interferencia y de refracción se fundan sobre el hecho de que ondas luminosas llegan al mismo punto por caminos diferentes, y allí se superponen; la refracción en el límite de dos cuerpos se produce por la diferencia de la velocidad de la luz en ellos; por tanto, ésta colabora en el efecto de todos los aparatos ópticos, lentes, prismas, etc. ¿No podrían inventarse dispositivos que pusiesen de manifiesto el movimiento de la Tierra y el «viento de éter» producido por él?

Se han inventado, en efecto, y realizado muchos experimentos para descubrir ese movimiento. Una experiencia general enseña que en experimentos hechos con focos luminosos terrestres nunca se ha notado el menor influjo del «viento de éter»; también se han dispuesto experimentos especiales que demuestran eso. Desde luego, hasta hace poco, se trataba de experimentos dispuestos de manera que sólo podían apreciar cantidades de primer orden en β. Si han dado siempre un resultado negativo, esto obedece a que en ellos no se ha medido nunca la verdadera duración del movimiento de la luz de un punto a otro, sino sólo diferencias de tiempos para el mismo camino de la luz o sus sumas al recorrer el camino de ida y vuelta; al proceder así, resulta, por el motivo ya arriba explicado, que las cantidades de primer orden se eliminan.

fig71

Pero podría esperarse un resultado positivo tomando un foco luminoso no terrestre, sino astronómico. Si se dirige un telescopio a una estrella a la cual se dirige (fig. 71) la velocidad momentánea v de la Tierra, entonces la velocidad de la luz en las lentes del telescopio con relación a la substancia del vidrio será v veces más grande que si la Tierra está inmóvil; y si se mira a la misma estrella medio año después con el mismo telescopio, entonces la velocidad de la luz en las lentes será v veces más pequeña. Ahora bien; la cantidad de refracción en una lente está determinada por la velocidad de la luz; podría, pues, esperarse que el foco de la lente en ambos casos tenga una posición diferente. Este seria un efecto del primer orden, pues la diferencia de la velocidad de la luz, en ambos casos, sería 2v, y su relación con la velocidad en el éter inmóvil $tfrac{2v}{c}=2\beta$.

Arago ha realizado, efectivamente, este experimento; pero no ha encontrado ninguna diferencia en la posición de los focos. ¿Cómo explicar esto?

Antes hemos hecho, evidentemente, la suposición de que la velocidad de la luz en un cuerpo que se mueve con respecto al éter, al encuentro del rayo, con la velocidad v, es mayor y justamente en la cantidad v, que si el cuerpo estuviera inmóvil en el éter. Dicho de otro modo: hemos admitido que el cuerpo material pasa a través del éter sin llevárselo consigo en lo más mínimo, como una red va por el agua del mar tirada por el bote pesquero.

El resultado del experimento enseña que tal no es el caso. Más bien ha de tomar parte el éter en el movimiento de la materia; la cuestión es saber en qué cantidad.

Fresnel determinó que para explicar la observación de Arago y todos los demás efectos del primer orden basta que el éter sea arrastrado sólo en parte por la materia. Vamos a exponer esta teoría, que fué más tarde brillantemente confirmada por la experiencia.

El punto de vista, más radical, de que el éter toma parte enteramente en el movimiento de la materia, lo ha defendido más tarde, sobre todo, Stokes (1845). Este físico admitió que la Tierra arrastra consigo, en su interior, el éter, y que ese movimiento del éter va poco a poco disminuyendo hacia afuera, hasta llegar a la inmovilidad del éter cósmico. Es claro que, en tal caso, todos los fenómenos luminosos en la Tierra verifícanse exactamente como si ésta fuese inmóvil; pero para que la luz procedente de las estrellas no sufra desviaciones y variaciones de velocidad al pasar por la capa que separa el éter cósmico del éter arrastrado con la Tierra, hace falta hacer hipótesis especiales sobre los movimientos del éter. Stokes discurrió una que satisface a todas las condiciones ópticas; pero luego se demostró que no concordaba con las leyes de la mecánica. Los numerosos intentos realizados para salvar la teoría de Stokes no han tenido éxito bueno, y hubiera sucumbido a las dificultades que encerraba, aun cuando el experimento de Fizeau (véase pág. 152) no hubiese venido a confirmar la teoría de Fresnel.

fig72

El pensamiento de Fresnel, según el cual la materia arrastra parcialmente al éter consigo, no es fácil de derivar del experimento de Arago, porque la refracción en las lentes es un proceso intrincado que toca no sólo a la velocidad, sino también a la dirección de las ondas. Pero existe un experimento de idéntico valor, que fué realizado por Hoek (1868) más tarde, y que es muchísimo más claro. Se deriva en principio de la disposición siguiente del interferómetro (fig. 72). Del foco luminoso Q sale la luz e incide en una lámina de vidrio P, plateada para ser semitransparente e inclinada 45º sobre la dirección del rayo luminoso; el rayo es dividido en dos; el rayo reflejado (rayo 1) va cayendo sucesivamente en los espejos S₁, S₂, S₃, los cuales forman con la lámina P un rectángulo, y al volver a P es en parte reflejado en la lente de observación F; el rayo que atraviesa P (rayo 2) recorre el mismo camino en sentido inverso, y llega al campo visual en interferencia con el rayo 1. Entre S₁ y S₂ se ha colocado un cuerpo transparente; v. gr., un tubo de vidrio lleno de agua, W, y todo el aparato está montado de modo que la dirección de S₁ a S₂ pueda variarse de manera a ser sucesivamente paralela y contraria al movimiento de la Tierra alrededor del Sol.

Sea c₁ la velocidad de la luz en el agua quieta; este valor es algo más pequeño que la velocidad en el vacío, y la relación de ambas velocidades, ${\tfrac {c}{c_{1}}}=n$, se llama índice de refracción. La velocidad en el aire es diferente de c en una insignificante inobservable cantidad; el índice de refracción del aire es casi exactamente 1. Ahora, el agua es arrastrada por la Tierra en su trayectoria. Si el éter que está en el agua no tomase parte en este movimiento, sería la velocidad de la luz en el agua, relativamente al éter cósmico, invariablemente c₁; esto es, sería c₁ - v para un rayo que marchase relativamente a la Tierra en la dirección del movimiento de la Tierra; si el éter fuese totalmente arrastrado por el agua, la velocidad de la luz, relativamente al éter cósmico, seria c₁ + v, y relativamente a la Tierra, c₁. No admitiremos a priori ninguna de las dos posibilidades, sino que dejaremos indeterminada la cantidad de éter que el agua arrastre; sea la velocidad de la luz en el agua, movida relativamente al éter cósmico, algo mayor que c₁, por ejemplo, c₁ + φ; esto es, sea, relativamente a la Tierra, c₁ + φ - v. Queremos encontrar, por el experimento, el desconocido número φ, que representa el arrastre de éter por el agua. Si φ es igual a cero, no habrá arrastre ninguno; si es igual a v, el arrastre será total; su valor verdadero tiene que estar entre esos dos limites. Pero vamos a admitir una sola cosa: que el arrastre por el aire es despreciable comparado con el arrastre por el agua.

Sea, pues, l la longitud del tubo lleno de agua; el rayo 1 necesita, para recorrer el tubo, el tiempo ${\tfrac {l}{c_{1}+\varphi -v}}$, cuando la Tierra se mueve en la dirección de S₁ hacia S₂; este mismo rayo necesita, para recorrer la correspondiente distancia entre S₃ y P, en donde no hay mas que aire, el tiempo ${\tfrac {l}{c+v}}$; en total, el tiempo que el rayo 1 necesita para recorrer los dos trechos iguales uno en agua y el otro en aire, es:

${\frac {l}{c_{1}+\varphi -v}}+{\frac {l}{c+v}}$.

El rayo 2 sigue el camino inverso; recorre primero el trecho de aire en el tiempo ${\tfrac {l}{c-v}}$, y luego el trecho de agua en el tiempo ${\tfrac {l}{c_{1}-\varphi +v}}$, y en total necesita, para los dos trechos iguales de aire y de agua, el tiempo

${\frac {l}{c-v}}+{\frac {l}{c_{1}-\varphi +v}}$.

Ahora bien; el experimento demuestra que las interferencias no varían lo más mínimo cuando el aparato gira en dirección opuesta o en cualquier otra dirección, respecto de la velocidad de la Tierra. De aquí se infiere que los rayos 1 y 2 necesitan iguales tiempos, independientemente de la orientación del aparato respecto de la trayectoria terrestre, y, por lo tanto, que

${\frac {l}{c_{1}+\varphi -v}}+{\frac {l}{c+v}}={\frac {l}{c-v}}+{\frac {l}{c_{1}-\varphi +v}}$.

Por esta ecuación es posible calcular φ; suprimiremos este cálculo algo circunstanciado ^[1] y daremos solamente el resultado, que, despreciando cantidades de segundo y más alto orden, dice:

$\varphi =(1-{\frac {1}{n^{2}}})v$.[39]

Esta es la famosa fórmula de arrastre de Fresnel, quien la encontró por otro camino más especulativo. Antes de decir su evaluación, determinemos lo que la fórmula expresa propiamente. El arrastre es, según ella, tanto mayor cuanto más excede de 1—valor que en el vacío tiene—el exponente de refracción. Para el aire es c₁ casi igual a c, n es casi igual a 1 y φ es, por lo tanto, casi igual a cero, como antes hubimos de suponer. Pero cuanto mayor sea la facultad de refractar la luz, tanto más completo será el arrastre. La velocidad de la luz en un cuerpo en movimiento es, pues, medida relativamente al éter cósmico,

$c_{1}+\varphi =c_{1}+(1-{\frac {1}{n^{2}}})v$,

y relativamente al cuerpo en movimiento:

$c_{1}+\varphi -v=c_{1}+(1-{\frac {1}{n^{2}}})v-v=c_{1}-{\frac {v}{n^{2}}}$.

A esta última fórmula referimos la interpretación de Fresnel.

Este admitió que la densidad del éter en un cuerpo material es diferente de la densidad del éter libre; la primera sea ρ₁ la segunda, ρ.

fig73

Representémonos el cuerpo en la forma, por ejemplo, de un madero cuya dirección longitudinal es paralela a la velocidad; su superficie base sea igual a la unidad de superficie. Al moverse el madero por el éter, la superficie delantera avanza en la unidad de tiempo la distancia v (figura 73) y ocupa un volumen v (la base unidad por la altura); en este volumen está contenida la cantidad de éter, ρv, que entra en el cuerpo por la superficie delantera. En el cuerpo toma otra densidad y, por tanto, se moverá, con respecto al cuerpo, con otra velocidad v₁; por el mismo motivo que más arriba, será su masa igual a ρ₁v₁, y puede escribirse

$\rho _{1}v_{1}=\rho v$

o

$v_{1}={\frac {\rho }{\rho _{1}}}v$.

Esta es, en cierto modo, la fuerza del viento de éter en el madero movido con la velocidad v. La luz que con respecto al éter condensado tiene la velocidad c₁ y tiene, con respecto al cuerpo, la velocidad

$c_{1}-v_{1}=c_{1}-{\frac {\rho }{\rho _{1}}}v$.

Pero hemos visto que, según los resultados del experimento de Hoek, la velocidad de la luz con respecto a los cuerpos en movimiento vale:

$c_{1}-{\frac {1}{n^{2}}}v$.

Por consiguiente,

${\frac {\rho }{\rho _{1}}}={\frac {1}{n^{2}}}={\frac {c_{1}^{2}}{c^{2}}}$

la condensación ${\tfrac {\rho _{1}}{\rho }}$ es, pues, igual al cuadrado del índice de refracción.

Aquí se puede seguir infiriendo que la elasticidad del éter en todos los cuerpos ha de ser la misma, pues la fórmula [33] (página 132) enseña que en todo medio elástico $c^{2}={\tfrac {p}{\rho }}$. Así, pues, en el éter $p=c_{1}\rho$ y en la materia $p_{1}=c_{1}^{2}\rho _{1}$; pero estas dos expresiones son iguales, según el anterior resultado acerca de la condensación.

Esta interpretación mecánica de la cantidad del arrastre por Fresnel ha tenido una gran influencia sobre la estructura de la teoría elástica de la luz. Pero no debemos ocultar que se le pueden dirigir importantes objeciones. Es sabido que luces de diferentes colores (números de vibraciones) tienen diferente refractabilidad n y, por tanto, diferente velocidad. De aquí se sigue que la cantidad del arrastre tiene un valor diferente para cada color. Mas esto es inconciliable con la interpretación de Fresnel, pues el éter debería verterse en el cuerpo con diferente velocidad según el color; habría, pues, tantos éteres como colores, y esto es imposible.

Pero, sin referirse a la interpretación mecánica, la fórmula del arrastre [39] está fundada en los resultados de experimentos. Veremos que, en la teoría electromagnética de la luz, está derivada de representaciones sobre la estructura atomística y de la electricidad.

Comprobar la fórmula de Fresnel por medio de experimentos terrestres es dificilísimo, porque necesítanse para ello substancias transparentes, movidas con gran rapidez. El experimento consiguió hacerlo Fizeau (1851) merced a un muy sensible dispositivo del interferómetro.

fig74

El aparato empleado por él es igual al de Hoek; pero los dos caminos que la luz recorre, S₁S₂ y S₃P, llevan tubos de vidrio, por los cuales puede correr agua, de manera que el rayo 1 marcha en el sentido del agua y el rayo 2 en contra de ésta (fig. 74). Fizeau examinó si el agua arrastra consigo la luz, observando si las interferencias se desplazan cuando el agua se pone en rápido movimiento. Y, en efecto, tal sucede, pero ni mucho menos en la medida que corresponde a un total arrastre; la medición exacta dió por resultado una perfecta concordancia con la fórmula de arrastre establecida por Fresnel [39].

10. La aberración.

Vamos ahora a discutir la influencia que el movimiento de los cuerpos tiene sobre la dirección de los rayos luminosos, y particularmente el problema de si puede comprobarse el movimiento de la Tierra a través del éter por medio de observaciones de variación en la dirección. Sobre esto hay que distinguir también si se trata de un foco luminoso terrestre o astronómico.

fig75

La aparente desviación de la luz, que llega a la Tierra procedente de las estrellas fijas, es la aberración, que ya hemos discutido desde el punto de vista de la teoría de la emisión (IV, 3, pág. 109). Tan sencilla como es la explicación dada allí, tan complicada en cambio es la cuestión desde el punto de vista de la teoría ondulatoria. Pues fácilmente se ve que una desviación de los planos de onda no se verifica en general. Clarísimamente se ve ello cuando los rayos caen perpendiculares al movimiento del observador; en tal caso, los planos de onda son paralelos a ese movimiento, y son percibidos igualmente por el observador en movimiento (fig. 75). Otro tanto nos enseña el cálculo. Colocamos un sistema inmóvil de coordenadas S y otro en movimiento S', de manera que el eje de las x y, respectivamente, de las x' caiga en la dirección del movimiento, y contamos las ondas que han pasado por un punto cualquiera P desde el instante t = 0 hasta el instante t; este número es, como sabemos, $\nu (t-{\tfrac {s}{c}})$, siendo s el camino recorrido por las ondas. Es evidente que, en el caso de ondas perpendiculares, s=y.

La invariancia del número de ondas exige que

$\nu (t-{\frac {y}{c}})=\nu '(t-{\frac {y'}{c'}})$,

cuando las coordenadas se calculan con la transformación de Galileo. Pero en ésta la coordenada y permanece invariable; por tanto, debe ser:

{{c|$\nu =\nu '$ y ${\frac {v}{c}}={\frac {v'}{c'}}$; y, por tanto, $c=c'$.}

El observador en movimiento ve, pues, una onda de igual frecuencia, velocidad y dirección; pues si ésta estuviese cambiada, tendría que depender el número de ondas en S', de x' además de y'.

Parece, pues, que la teoría ondulatoria no está en condiciones de explicar el hecho, sencillo y conocido desde hace doscientos años, de la aberración.

Pero la cosa no es tan desesperada. El fundamento que explica el fracaso de la reflexión que hemos hecho es que los instrumentos ópticos con que se hacen las observaciones, y entre ellos la simple vista, no determinan la posición del frente de ondas incidente, sino que realizan muy diferente labor.

Caracterizase la función del ojo o del telescopio por ser una reproducción óptica, y consiste en que los rayos procedentes de un objeto iluminado se reúnen en una imagen. Al acontecer esto, la energía vibratoria de las partículas del objeto es transportada por las ondas luminosas hacia las partes correspondientes de la imagen. Los caminos de ese transporte de energía son, efectivamente, los rayos físicos. Mas la energía es una cantidad que, según la ley de conservación, puede, como una substancia, transformarse, pero ni nacer ni desaparecer. Por lo cual es plausible que puedan aplicarse a su movimiento las leyes de la teoría de la emisión. Efectivamente, la sencilla deducción que antes hicimos (pág. 110) de la fórmula de aberración es totalmente exacta, si se definen los rayos luminosos como las trayectorias de energía de las ondas luminosas, y se les aplica las leyes del movimiento relativo, como si fueran torrentes de partículas desprendidas.

Pero también se puede llegar a la fórmula de aberración sin aplicar este concepto de los rayos como trayectorias de energía; para ello se persigue una por una la refracción de las ondas en las lentes o los prismas de los instrumentos ópticos. En tal caso, hay que partir de una determinada teoría del arrastre. La teoría de Stokes, que admite el integral o total arrastre, no explica la aberración sino haciendo sobre el movimiento del éter hipótesis inaceptables mecánicamente; ya más arriba hemos hablado de estas dificultades. La teoría de Fresnel proporciona una ley de refracción de las ondas luminosas en la superficie de cuerpos en movimiento, por la cual se obtiene exactamente la fórmula de aberración.

La substancia de los cuerpos a través de los cuales pasa la luz no influye en el resultado, aun cuando la cantidad del arrastre es distinta en cada substancia. Para probarlo, Airy (1871) llenó de agua un telescopio y estableció que, a pesar de ello, la aberración tenia su cantidad normal. La aberración, como efecto de primer orden, desaparece naturalmente cuando la onda luminosa y el observador no tienen ningún movimiento relativo uno a otro. De aquí se sigue que en los experimentos ópticos con focos luminosos terrestres no se verifica ninguna desviación de los rayos por el viento de éter. La teoría de Fresnel está en condiciones de exponer estos hechos en concordancia con la experiencia. Queda para otra ocasión volver detenidamente sobre este punto.

Interrumpamos ahora nuestras explicaciones acerca del éter luminoso y lancemos una mirada a los conocimientos adquiridos.

11. Recapitulación y nueva perspectiva.

Hemos tratado el éter luminoso como una substancia que obedece a las leyes de la mecánica. Satisface, pues, a la ley de inercia y, por tanto, allí donde no haya materia, en el espacio cósmico, hallaráse inmóvil en un apropiado sistema inercial. Si ahora referimos todos los fenómenos a otro sistema inercial, seguirán valiendo las mismas leyes para los movimientos de los cuerpos y del éter; por tanto, también para la propagación de la luz, aunque naturalmente sólo en cuanto se refieran a aceleraciones y acciones recíprocas. Sabemos que la velocidad y la dirección de un movimiento son totalmente diferentes con respecto a diferentes sistemas inerciales; se puede considerar a todo cuerpo en movimiento rectilíneo uniforme, como inmóvil, eligiendo un sistema de referencia apropiado, que se mueva con el cuerpo. En este sentido, casi trivial, debe, pues, el principio clásico de la relatividad valer también para el éter pensado como substancia mecánica.

De aquí se infiere, empero, que la velocidad y dirección de los rayos luminosos deben aparecer distintas en cada sistema inercial. Seria, pues, de esperar que, por observaciones de los fenómenos ópticos terrestres, que están principalmente determinados por la velocidad y dirección de la luz, se estableciese la velocidad de la Tierra o del sistema solar. Pero todos los experimentos hechos con tal propósito han dado un resultado negativo. Queda, pues, como conclusión, que la velocidad y dirección de los rayos luminosos son del todo independientes del movimiento del cuerpo cósmico sobre el cual se establecen las observaciones. O, dicho de otro modo, los fenómenos ópticos no dependen mas que de los movimientos relativos de los cuerpos materiales.

Es éste un principio de relatividad que suena muy semejante al principio clásico de la mecánica; pero tiene un sentido diferente, pues se refiere a velocidades y direcciones de procesos de movimiento, y éstas, en la mecánica, no son independientes del movimiento del sistema de referencia.

Sólo hay dos puntos de vista posibles. El primero parte de la consideración de que las experiencias ópticas nos dan algo nuevo en principio, a saber: que la luz se conduce, por lo que a velocidad y dirección se refiere, de distinto modo que los cuerpos materiales. Si se consideran las experiencias ópticas como coactivas, como imponiéndose a nosotros, habrá de defender el físico este punto de vista, si quiere mantenerse lejos de toda especulación sobre la esencia de la luz. Ya veremos que éste es el camino que en definitiva ha seguido Einstein. Pero se necesita para ello una altísima libertad frente a las convenciones de las teorías tradicionales, libertad que sólo es posible cuando el nudo gordiano de construcciones e hipótesis ha llegado a tal complicación que la solución única es cortarlo de un tajo.

Pero aun estamos aquí en plena época floreciente de la teoría mecánica del éter; y esta teoría tomó, naturalmente, el otro punto de vista. Debía concebir el principio óptico de relatividad como fenómeno secundario, y en cierto modo semicontingente, producido por la compensación de causas eficientes actuando retroactivamente. Que esto es, hasta cierto punto, posible, obedece a que hay libertad de hacer hipótesis acerca de cómo el éter se mueve, de cómo es influido en su movimiento por los cuerpos en movimiento. Ahora bien; un gran resultado de la hipótesis de Fresnel sobre el arrastre del éter es que ella explica, efectivamente, el principio de la relatividad óptica, en cuanto que se refiere a cantidades del primer orden. Mientras la exactitud de las mediciones ópticas no recibió la poderosa impulsión que es necesaria para medir cantidades del segundo orden, aquella teoría de Fresnel satisfacía a todas las exigencias de la experiencia, salvo una posible excepción, poco notada, por lo general, lo cual es bastante extraño y admirable. En efecto; si la exactitud perfeccionada de las mediciones astronómicas llegare al resultado de que la observación de los eclipses de los satélites de Júpiter según el antiguo método de Römer (véase pág. 147) no señala un influjo del movimiento del sistema solar sobre la velocidad de la luz, hallaríase la teoría del éter ante un problema casi insoluble, pues es bien claro que ese efecto del primer orden no podría anularse por ninguna hipótesis sobre arrastre del éter.

Compréndese, pues, la importancia del problema experimental, que consiste en medir hasta en cantidades del segundo orden la dependencia en que están los procesos ópticos del movimiento de la Tierra. La solución de este problema sería la que pudiese decidir si el principio de la relatividad óptica vale estrictamente o sólo aproximadamente. En el primer caso, fallaría la teoría de Fresnel sobre el éter; nos hallaríamos ante una situación nueva.

Históricamente, esta situación nueva se ha presentado unos cien años después de Fresnel. Entre tanto, hay una evolución de la teoría del éter en otra dirección. Al principio, en efecto, no había un éter solamente, sino muchos: uno óptico, uno térmico, uno eléctrico, uno magnético y aun quizá más todavía. Para cada fenómeno que se verifica en el espacio inventábase como sustentáculo un éter especial. Estos éteres no tenían al principio nada de común entre sí, sino que existían en el mismo espacio independientemente unos de otros, o, mejor dicho, dentro unos de otros. Tal estado de la física no podía durar, naturalmente. Pronto se encontraron conexiones entre los fenómenos de las distintas esferas, separados en un principio, y así resultó, finalmente, un éter único como sustentáculo de todos los fenómenos físicos que se verifican en el espacio libre de materia. Particularmente manifestóse la luz como un proceso vibrátil electromagnético, cuyo sustentáculo es idéntico al medio que transmite las fuerzas eléctricas y magnéticas. Estos descubrimientos fueron primeramente un buen puntal para la noción del éter. Por último, llegóse incluso a identificar el éter con el espacio de Newton; permanecería en inmovilidad absoluta y transmitiría no sólo los efectos electromagnéticos, sino que produciría también, mediatamente, las fuerzas newtonianas de inercia y centrífugas.

Ahora pasamos a exponer esta evolución de la teoría. Es como una emocionante sesión ante el tribunal de justicia; el éter ha de ser el culpable de todo; amontónanse pruebas sobre pruebas, hasta que, por último, la irrefragable demostración de la coartada pone término a la causa. Esta demostración definitiva es el experimento de Michelson sobre cantidades del segundo orden y su interpretación por Einstein.

---

1. Conclúyese por la serie:
   ${\frac {(c+v)+(c_{1}+\varphi -v)}{(c_{1}+\varphi -v)(c+v)}}={\frac {(c_{1}-\varphi +v)+(c-v)}{(c-v)(c_{1}-\varphi +v)}}$,
   $(c+c_{1}+\varphi )(c-v)(c_{1}-\varphi +v)=(c+c_{1}-\varphi )(c+v)(c_{1}+\varphi -v)$,
   $\varphi ^{2}-\varphi {\frac {v^{2}+c^{2}}{v}}=c_{1}^{2}-c^{2}$

   y aproximadamente:

   $\varphi ={\frac {v}{2\beta ^{2}}}(1+\beta ^{2}-{\sqrt {(1-\beta ^{2})^{2}+{\frac {4\beta ^{2}}{n^{2}}}}})$,
   $\varphi ={\frac {v}{2\beta ^{2}}}[1+\beta ^{2}-(1-\beta ^{2}+{\frac {2\beta ^{2}}{n^{2}}})]$,
   $\varphi =(1-{\frac {1}{n^{2}}})v$.