Almagesto: Libro III - Capítulo 06
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
{Sobre la construcción de una tabla para subdivisiones individuales de la Anomalía}
Con el fin de permitirle a uno determinar el Movimiento Anomalístico sobre cualquiera de las subdivisiones [del círculo], demostraremos, nuevamente por ambas hipótesis, como, dado uno de los arcos en cuestión, podemos calcular los otros.
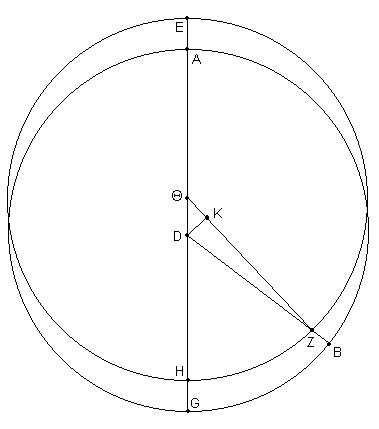
[Ver Fig. 3.12.] Primero, sea ABG el círculo concéntrico a la Eclíptica, con centro en D, la Excéntrica EZH con centro en Θ, y sea EAΘDH el diámetro a través de ambos centros y el apogeo E. Cortar el arco EZ, y unir ZD, ZΘ. Primero, sea dado el arco EZ, por ej. de 30º.

Prolongar ZΘ y eliminar DK, la perpendicular a él ([ZΘ]) desde D.
Entonces, dado que el arco EZ es, por hipótesis, de 30º.
^ EΘZ = ^ DΘK = 30º donde 4 ángulos rectos = 360º
^ EΘZ = ^ DΘK = 60ºº donde 2 ángulos rectos = 360ºº.
Por lo tanto, en el círculo alrededor del triángulo rectángulo DΘK,
arco DK = 60°
y el arco KΘ = 120° (su suplementario).
En consecuencia las cuerdas correspondientes
arco DK = 60p donde la hipotenusa DΘ = 120p
y KΘ = 103;55p donde la hipotenusa DΘ = 120p.
Por lo tanto, donde DΘ = 2;30p y el radio ZΘ = 60p,
DK = 1;15p y ΘK = 2;10p.
Por lo tanto, por adición [de ΘK al radio ZΘ], KΘZ = 62;10p.
Ahora dado que DK² + KΘZ² = ZD²,
la hipotenusa ZD ≈ 62;11p.
Por lo tanto, donde ZD = 120p, DK = 2;25p,
y, en el círculo alrededor del triángulo rectángulo ZDK,
el arco DK = 2;18º.
en consecuencia ^ DZK = 2;18ºº donde 2 ángulos rectos = 360ºº
por lo tanto ^ DZK = 1;9º donde 4 ángulos rectos = 360º.
Este [1;9º] será la cantidad de la ecuación de la anomalía en esa posición.
Y el ^ EΘZ fue tomado como de 30º.
Por lo tanto, por sustracción, el ^ ADB (que es igual al arco AB de la eclíptica) es igual a 28;51º .
Además; si es dado cualquiera de los otros ángulos [relevantes, en cambio del ^ EΘZ], los ángulos restantes serán dados, como es inmediatamente obvio si, en la misma figura [ver Fig. 3.13] eliminamos la perpendicular ΘL desde Θ hasta ZD.

Porque supongamos primero que es dado el arco AB de la eclíptica, por ej. el ^ ΘDL. Entonces la proporción DΘ / ΘL será dada [2]. Y dado que también es dada [la proporción] DΘ / ΘZ, será dada la ΘZ / ΘL [3]. Por lo tanto el ^ ΘZL, la Ecuación de la Anomalía, será dada [4], y también lo será el ^ EΘZ, por ej. el arco EZ de la excéntrica.
O supongamos, en (segundo) lugar, que es dada la ecuación de la anomalía, por ej. el ^ ΘZD: tomaremos los mismos resultados en orden inverso. Desde el ^ ΘZD será dada la proporción ΘZ / ΘL, y la [proporción] ΘZ / ΘD se da desde el principio. En consecuencia DΘ / ΘL será dada, y por lo tanto el ^ ΘDL, por ej. del arco AB de la eclíptica, y [por ende] el ^ EΘZ, por ej. del arco EZ de la excéntrica.
Seguidamente [ver fig. 3.14] sea ABG el círculo concéntrico con el eclíptica, con centro en D y diámetro ADG, y sea el epiciclo EZHΘ con centro en A (en la misma proporción [al círculo ABG como la excentricidad de la excéntrica]). Cortar el arco EZ y unir ZBD y ZA. Nuevamente sea el arco EZ tomado por la misma cantidad de 30º. Eliminar la perpendicular ZK desde Z hasta AE.

Dado que el arco EZ = 30º,
^ EAZ = 30º donde 4 ángulos rectos = 360º
^ EAZ = 60ºº donde 2 ángulos rectos = 360ºº.
Por lo tanto en el círculo alrededor del triángulo rectángulo AZK [inscripto] ,
arco ZK = 60º
y arco AK = 120º (su suplementario).
En consecuencia las cuerdas correspondientes
ZK = 60p donde el diámetro AZ = 120p.
y KA = 103;55p donde el diámetro AZ = 120p.
Por lo tanto donde la hipotenusa AZ = 2;30p y el radio AD = 60p
ZK = 1;15p, KA = 2;10p,
y, por adición, KAD = 62;10p.
Y dado que ZK² + KD² = ZBD²,
ZD = 62;11p, donde ZK = 1;15p.
Entonces donde la hipotenusa DZ = 120p, ZK = 2;25p,
y, en el círculo alrededor del triángulo rectángulo DZK,
arco ZK = 2;18º.
En consecuencia ^ ZDK = 2;18ºº donde 4 ángulos rectos = 360ºº
por lo tanto ^ ZDK = 1;9º donde 2 ángulos rectos = 360º.
Esta es, nuevamente, la cantidad de la ecuación de la anomalía, que esta representada por el arco AB.
Y el ^ EAZ fue tomado como de 30º.
Por lo tanto, por sustracción, el ^ AZD, que representa el arco del Movimiento Aparente sobre la Eclíptica, es de 28;51º.
Estas cantidades están de acuerdo con las que hallamos en la Hipótesis de la Excéntrica.
Aquí también, si cualquier otro ángulo es dado [en cambio del ^ EAZ], los ángulos restantes serán dados, [como puede ser visto] en la misma figura [ver Fig. 3.15] si la perpendicular AL es eliminada desde A hasta DZ.

Porque si, como antes, primero tomamos el arco del movimiento aparente sobre la eclíptica, por ej. dado el ^ AZD, desde este será dada la proporción ZA / AL. Y ya que [la proporción] ZA / AD fue dada desde el principio, lo será [también] DA / AL. Por lo tanto el ^ ADB será dado, por ej. el arco AB, arco de la ecuación de la anomalía, y también lo será el ^ EAZ, por ej. el arco EZ del epiciclo.
O si, Segundo, tomamos la ecuación de la anomalía, por ej. dado el ^ ADB, entonces, por el mismo camino pero en orden inverso, desde este [ángulo] será dada [la proporción] AD / AL; y ya que DA / AZ fue dada desde el principio, lo será también ZA / AL; y por lo tanto será dado el ^ AZD, que corresponde al arco del movimiento aparente sobre la eclíptica, y también lo será el ^ EAZ, por ej. el arco EZ del epiciclo.
Tomemos nuevamente la figura anterior de la excéntrica [ver Fig. 3.16], y cortar desde H, el perigeo de la excéntrica, el arco HZ, que nuevamente tomamos como de 30º. Unir DZB y ZΘ, y eliminar la perpendicular DK desde D hasta ΘZ.
Luego dado que el arco ZH es = a 30º,
^ ZΘH = 30º donde 4 ángulos rectos = 360º
^ ZΘH = 60º donde 2 ángulos rectos = 360ºº.
Por lo tanto en el círculo alrededor del triángulo rectángulo DΘK,
arco DK = 60º
y arco KΘ = 120º (su suplemento).
Por lo tanto las cuerdas correspondientes
DK = 60p donde el diámetro DΘ = 120p
y KΘ = 103;55p donde el diámetro DΘ = 120p.
Por lo tanto donde la hipotenusa DΘ = 2;30p y el radio ΘZ = 60p,
DK = 1;15p y ΘK = 2;10p,
y KZ = 57;50p por sustracción [de ΘK desde ΘZ].
Y ya que DZ² = DK² + KZ²,
DZ ≈ 57;51p donde DK = 1;15p.
Por lo tanto donde la hipotenusa DZ = 120p, DK = 2;34p. [5].
Y, en el círculo alrededor del triángulo rectángulo DZK,
arco DK = 2;27º.
En consecuencia ^ DZK = 2;27ºº donde 2 ángulos rectos = 360ºº
por lo tanto ^ DZK = 1;14º (aproximadamente) donde 4 ángulos rectos = 360º.
Estos [1;14º], son entonces, la ecuación de la anomalía.
Y dado que el ^ ZΘH fue tomado como de 30º, por adición, el ^ BDG, por ej. el arco GB de la eclíptica, es igual a 31;14º.
Aquí también, por el mismo camino [como antes], [ver Fig. 3.17] prolongamos BD y eliminamos ΘL hacia él [(BD)].

Entonces si, primero, tomamos como dado el arco GB de la eclíptica, por ej. el ^ ΘDL, desde este será dada la proporción DΘ / ΘL. Y ya que ΘD / ΘZ fue también dada desde el comienzo, será dada ZΘ / ΘL. Por lo tanto tendremos como dados los ángulos
^ ΘZD, por ej. la ecuación de la anomalía y el ^ ZΘD, por ej. el arco HZ de la excéntrica.
O si, segundo, tomamos como dada la ecuación de la anomalía, por ej. el ^ ΘZD, entonces recíprocamente, desde este será dada [la proporción] ZΘ / ΘL. Y ya que ZΘ / ΘD fue también dada desde el comienzo, lo será DΘ / ΘL. Por lo tanto tendremos, como ángulos dados,
el ^ ΘDL, que corresponde al arco GB de la eclíptica y el ^ ZΘH, por ej. el arco HZ de la excéntrica.
Similarmente, sobre la figura anterior de la Concéntrica y del Epiciclo [ver Fig. 3.18], cortamos el arco ΘH desde el Perigeo, por la misma cantidad de 30º, [y] unir AH y DHB, y eliminar la perpendicular HK desde H hasta AD.
Entonces, dado que el arco ΘH es nuevamente de 30º,
^ ΘAH = 30º donde 4 ángulos rectos = 360º
^ ΘAH = 60ºº donde 2 ángulos rectos = 360ºº.
Por lo tanto en el triángulo rectángulo HKA, [inscripto en el círculo EZHΘ]
arco HK = 60º
y arco AK = 120º (su suplementario).

Por lo tanto las cuerdas correspondientes
HK = 60p donde la hipotenusa AH = 120p
y AK = 103;55p donde la hipotenusa AH = 120p.
Por lo tanto donde AH = 2;30p y el radio AD = 60p,
HK = 1;15p, AK = 2;10p y KD = 57;50p, por sustracción.
y ya que HK² + KD² = DH²,
DH ≈ 57;51p donde KH = 1;15p.
Por lo tanto donde la hipotenusa DH = 120p
HK = 2;34p,
y, en el círculo siendo DHK, el arco HK = 2;27º.
En consecuencia ^ HDK = 2;27ºº donde 2 ángulos rectos = 360ºº
por lo tanto ^ HDK = 1;14º donde (aproximadamente) 4 ángulos rectos = 360º.
Aquí también, entonces, este es el tamaño de la ecuación de la anomalía, por ej. el arco AB.
Y ya que el ^ KAH fue tomado como de 30º, por adición, el ^ BHA es de 31;14º, que representa el movimiento aparente sobre la eclíptica [contado desde el perigeo]. Estas cantidades están de acuerdo con aquellas halladas en la [hipótesis] de la excéntrica.
Aquí también, por el mismo camino [como el de antes], eliminamos la perpendicular AL hasta DB [ver Fig. 3.19].
Entonces si, primero, tomamos como dado el arco de la eclíptica, por ej. el ^ AHL, desde este será dada la proporción HA / AL. Y ya que HA / AD fue dada desde el principio, lo será DA / AL. Por consiguiente tendremos como dados los ángulos
el ^ ADB, por ej. el arco AB, representando la ecuación de la anomalía
y ^ ΘAH, por ej. el arco ΘH del epiciclo.

O si, segundo, tomamos como dado el arco AB, representando la ecuación de la anomalía, por ej. el ^ ADB, entonces, por el mismo camino pero en orden inverso, desde este será dada la proporción DA / AL. Y ya que [la proporción] DA / AH esta dada desde el principio, también será dada HA / AL.
Por consiguiente tendremos como dados los ángulos
el ^ AHL, por ej. el arco de la eclíptica y el ^ ΘAH, por ej. el arco ΘH del epiciclo.
Así hemos demostrado lo que nos propusimos hacer.
Con el fin de tener convenientemente disponible la cantidad de la corrección para cualquier posición dada, [queremos] establecer una tabla, subdividida dentro de secciones [apropiadas], para el cálculo de las posiciones aparentes de la anomalía. Los teoremas de arriba permitirán una amplia variedad [de éstas posiciones] en el formato de una tabla [6], aunque preferimos la forma en la que el argumento es el movimiento medio y la función es la ecuación de la anomalía [7]. Dado que este formato esta bien de acuerdo con las actuales teorías, y también brinda un simple pero muy práctico camino de cálculo para cualquier resultado deseado. Entonces, utilizando el primer conjunto de teoremas [por ej. el de la hipótesis de la excéntrica] que hemos utilizado en los ejemplos numéricos anteriores, calculamos geométricamente, por el camino descrito, para las subdivisiones individuales [del círculo], la ecuación de la anomalía correspondiente al arco del movimiento medio. En general, tanto para el Sol y como para los otros cuerpos, dividimos los cuadrantes cerca del apogeo [8] en 15 subdivisiones (por lo tanto en esos cuadrantes el intervalo de tabulación será de 6º), y los cuadrantes cerca del perigeo dentro de 30 subdivisiones (por ende en esas subdivisiones el intervalo de tabulación es de 3º). La proporción es que las diferencias entre las ecuaciones de las anomalías [sucesivas], para subdivisiones iguales [del argumento], son mayores cerca del perigeo que cerca del apogeo.
Estableceremos la tabla de la anomalía del Sol, entonces, en 45 líneas, como [lo hicimos] antes, y en 3 columnas. Las primeras dos columnas contendrán los números del movimiento medio a través de los 360º: las primeras 15 líneas comprenderán los dos cuadrantes cerca del apogeo, las 30 siguientes los dos cuadrantes cerca del perigeo. La tercera columna contendrá los grados de la ecuación de la anomalía a ser sumada o restada, correspondientes al movimiento medio apropiado. La tabla es la siguiente:
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Libro III |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 |
Notas de referencia
- ↑ Leer en H240,16-17, en el manuscrito D (cf. todos los manuscritos griegos en la tabla de contenidos, H190,9-10) en cambio de (“investigación de la anomalía para extensiones parciales”, que es la lectura en el manuscrito Ar en ambos lugares). Sobre los capítulos 5 y 6 ver HAMA 58-60, Pedersen 149-51.
- ↑ Euclides Data 40: si los ángulos de un triángulo son dados, sus lados están dados de la forma (por ej. la proporción de los lados es dada, cf. Data 3).
- ↑ Euclides Data 8: aquellas magnitudes teniendo una proporción dada para la misma magnitud tienen una proporción dada la una para la otra. DQ / QZ esta dada como la proporción de la excentricidad.
- ↑ Euclides Data 43: si, en un triángulo rectángulo, los lados de uno de los ángulos agudos tienen una proporción dada, el triángulo se da en forma (cf. nota de referencia más arriba nro. 2).
- ↑ Leer en el manuscrito Ar, segmento segmento en cambio de segmento seg. seg. (2;34,36) en H247,6. Cálculos precisos dan 2;35,34 (cf. lectura en el manuscrito D²), aunque Ptolomeo solo da sus resultados en minutos, y 2;34 es el correcto, dado que Cuerda 2;27º = 2;33,55p ≈ 2;34p. El número 36 probablemente fue una corrección marginal al número 34 (cf. lectura en el manuscrito D en H249,20), que fue más tarde erróneamente incorporado como un lugar extra. La misma corrección ha sido realizada en H249,20 (ambas hechas por Manitius).
- ↑ Ptolomeo da a entender que uno teoricamente puede tomar como argumento tanto el movimiento medio (seg. ), la posición verdadera (), o la ecuación ().
- ↑ Literalmente “el cual contiene la ecuación de la anomalía correspondiente a los arcos del movimiento medio”.
- ↑ Leer (en todos los manuscritos) en cambio de (error de imprenta en el manuscrito de Heiberg) en H251,24. Corregida por Manitius.
