Almagesto: Libro III - Capítulo 05
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
{Sobre la Anomalía Aparente del Sol}
Habiendo establecido anteriormente los teoremas preliminares, debemos agregar una tesis preliminar adicional concerniente a la Anomalía Aparente del Sol. Esta tiene que ser solo una anomalía, de tal tipo donde el tiempo tomado desde la menor velocidad hasta la media siempre será mayor que el tiempo desde la velocidad media hasta la mayor, dado que encontramos que esto esta de acuerdo con el fenómeno. Ahora esto puede ser representado por ambas de las hipótesis descritas anteriormente, aunque en el caso de la Hipótesis del Epiciclo el movimiento del Sol sobre el arco del apogeo del epiciclo tendría que estar antes [expuesto].
Sin embargo, podría verse más razonable asociarlo con la Hipótesis de la Excéntrica ya que esta es más simple y se realiza por medio de un movimiento en cambio de dos [2].
Nuestra primera tarea es encontrar la proporción de la excentricidad del círculo [órbita (deferente)] del Sol, esto es, la proporción en la que la distancia entre el centro de la excéntrica y el centro de la eclíptica (localizada en el observador) mantiene [como resultado] el radio de la excéntrica. Debemos también hallar el grado de la eclíptica en el cual se ubica el apogeo de la excéntrica.
Estos problemas han sido resueltos por Hiparco con gran cuidado [3]. Él asume que el intervalo desde el Equinoccio de primavera hasta el Solsticio de verano es de 94 ½ días, y que el intervalo desde el solsticio de verano hasta el equinoccio de otoño es de 92 ½ días, y entonces, con esas observaciones como sus únicos datos, demuestra que el segmento de línea entre los centros arriba mencionados [de la excéntrica y la eclíptica] es de aproximadamente 1/24 parte del radio de la excéntrica, y que el apogeo esta aproximadamente a 24 ½º (donde la eclíptica esta dividida en 360º) antes del solsticio de verano. Nosotros también, en nuestro (propio) tiempo [(por el de Ptolomeo)], encontramos aproximadamente los mismos valores para los tiempos [que toma el Sol en atravesar] los cuadrantes arriba mencionados, y para aquellas proporciones. Por lo tanto para nosotros esta claro que la excéntrica del Sol siempre mantiene la misma posición relativa en los puntos solsticiales y equinocciales [4].
Con el fin de no desatender este tema, sino más bien mostrar el teorema elaborado de acuerdo con nuestra propia solución numérica, también resolveremos el problema para la excéntrica, utilizando los mismos datos observados, a saber, como los ya establecidos, de que el intervalo desde el equinoccio de primavera hasta el solsticio de verano comprende 94 ½ días, y que desde el solsticio de verano hasta el equinoccio de otoño, 92 ½ días. Nuestras observaciones muy precisas de [un] equinoccio y de [un] solsticio en el 463 er. año desde la muerte de Alejandro, se confirman los totales de días en esos intervalos: tal como hemos dicho Libro III Capítulo 2, el equinoccio de otoño ocurrió el 9 de Athyr [III] [26 Septiembre del 139], después de la salida del Sol, el equinoccio de primavera en el 7 de Pachon [IX] [22 de Marzo del 140], después del mediodía (por lo tanto el intervalo [entre ellos] es 178 ¼ días), y el solsticio de verano en el 11/12 de Mesore [XII], [24/25 de Junio del 140], después de la medianoche. Por lo tanto este intervalo, desde el equinoccio de primavera hasta el solsticio de verano, comprende 94 ½ días, lo que deja aproximadamente 92 ½ días para completar el año; este número representa el intervalo desde el solsticio de verano hasta el siguiente equinoccio otoñal [5].
[Ver Fig. 3.9] Sea ABGD la eclíptica con centro en E. En ella dibujamos dos diámetros, AG y BD, en ángulos rectos uno con el otro, a través de los puntos solsticiales y equinocciales. Sea A que representa el [equinoccio] de primavera, B el [solsticio] de verano, y así sucesivamente en orden.

Ahora esta claro que el centro de la excéntrica estará ubicado entre las líneas EA y EB. Dado que el semicírculo ABG comprende más de la mitad de la longitud de un año, y por lo tanto corta más que un semicírculo de la excéntrica; y el cuadrante AB también comprende un tiempo más largo y corta un arco mayor de la excéntrica que el cuadrante BG. Siendo esto así, sea Z el punto que representa el centro de la excéntrica, y dibujar el diámetro a través de ambos centros y del apogeo EZH. Con centro en Z y un radio arbitrario dibujar la excéntrica del Sol ΘKLM, y dibujar a través de Z las líneas NXO paralela a AG y la PRS paralela a BD. Dibujar la perpendicular ΘTY desde Θ a NXO y la perpendicular KFQ desde K hasta PRS.
Ahora dado que el Sol atraviesa el círculo ΘKLM con movimiento uniforme, este recorrerá el arco ΘK en 94 ½ días, y el arco KL en 92 ½ días. En 94 ½ días su movimiento medio es de aproximadamente 93;9º, y en 92 ½ días 91;11º. Por lo tanto
arco ΘKL = 184;20º
y, por sustracción del semicírculo NPO [del arco ΘKL],
arco NΘ + arco LO [= 184;20º - 180º] = 4;20º
Entonces arco ΘNY = 2 * arco ΘN = 4;20º también,
en consecuencia ΘY = Cuerda arco ΘNY ≈ 4;32p (*)
y EX = ΘT = ½ ΘY = 2;16p (*)
(*) donde el diámetro de la excéntrica es = 120p,
Ahora ya que arco ΘNPK = 93;9º,
y arco ΘN = 2;10º y cuadrante NP = 90º,
por sustracción, arco PK = 0;59º,
y arco KPQ = 2 * arco PK = 1;58º.
En consecuencia KFQ = Cuerda arco KPQ = 2;4p, (*)
y ZX = KF = ½ * KFQ = 1;2p (*)
(*) donde el diámetro de la excéntrica = 120p.
Y hemos demostrado que EX = 2;16p en las mismas unidades.
Ahora dado que EZ² = ZX² + EX²,
EZ ≈ 2;29 ½p donde el radio de la excéntrica es = 60p.
Por lo tanto el radio de la excéntrica es de aproximadamente 24 veces la distancia entre los centros de la excéntrica y de la eclíptica.
Ahora, ya que EZ / ZX = 2;29 ½ / 1;2,
ZX será alrededor de 49;46p donde la hipotenusa EZ = 120p.
Por lo tanto, en el círculo alrededor del triángulo rectángulo EZX,
arco ZX ≈ 49º.
En consecuencia ^ ZEX = 49ºº donde 2 ángulos rectos = 360ºº
por lo tanto ^ ZEX = 24;30º donde 4 ángulos rectos = 360º.
Entonces, dado que el ^ ZEX es un ángulo en el centro de la eclíptica [(ADGB)], el arco BH es también de 24;30º, que es la cantidad por la que el apogeo en H esta antes del solsticio de verano en B.
Además, dado que los cuadrantes OS y SN son cada uno de 90º,
y arco OL = arco ΘN = 2;10º,
y arco MS = 0;59º,
en consecuencia arco LM = 86;51º,
y arco MΘ = 88;49º.
Pero el Sol en su movimiento uniforme viaja
86;51º en alrededor de 88 ⅛ días,
y 88;49º en alrededor de 90 ⅛ días.
Por lo tanto esta claro que el Sol recorrerá el arco GD, que se extiende desde el equinoccio otoñal hasta el solsticio de invierno, por alrededor de 88 ⅛ días, y el arco DA, que se extiende desde el solsticio de invierno hasta el equinoccio de primavera, por alrededor de 90 ⅛ días. Las conclusiones anteriores están de acuerdo con lo que Hiparco dice.
Utilizando esas cantidades, entonces, permitámonos ver primero que la mayor diferencia entre los movimientos medio y anomalístico existe, y en qué puntos ocurrirá.
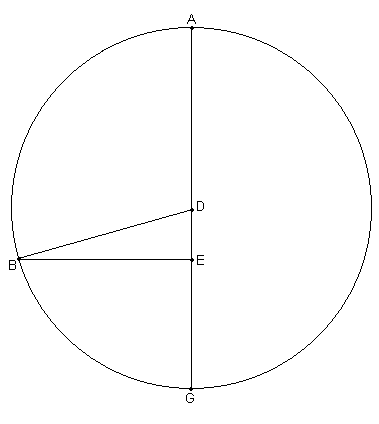
[Ver Fig. 3.10] Sea ABG el círculo excéntrico con centro en D y el diámetro ADG a través del apogeo A, sobre el cual E representa el centro de la eclíptica.
Dibujar EB en ángulos rectos hasta AG, y unir DB.
Ahora dado que, donde BD, el radio, igual a 60p, DE, la excentricidad, igual a 2;30p (de acuerdo a la proporción 24 / 1), [entonces] en el círculo alrededor del triángulo rectángulo BDE,
DE = 5p donde la hipotenusa BD = 120p,
y arco DE ≈ 4;46º.
Por lo tanto el ^ DBE, que representa la Máxima Ecuación de la Anomalía,
= 4;46ºº donde 2 ángulos rectos = 360ºº
= 2;23º donde 4 ángulos rectos = 360º.
En las mismas unidades, el ángulo recto BED = 90º,
y ^ BDA = ^ DBE + ^ BED = 92;23º.
Por lo tanto, dado que el ^ BDA esta en el centro de la excéntrica y el ^ BED esta en el centro de la eclíptica, concluimos que la máxima ecuación de la anomalía es de 2;23º, y la posición donde esta ocurre esta a 92;23º desde el apogeo, medido a lo largo de la excéntrica con un movimiento uniforme, y (como probamos en un principio) a un cuadrante, o a 90º [desde el apogeo], medido a lo largo de la eclíptica con un movimiento anomalístico. Es obvio desde nuestros resultados previos de que en el semicírculo opuesto [6] la velocidad media y la máxima ecuación de la anomalía ocurrirá en los 270º del movimiento aparente, y en los 267;37º de movimiento medio sobre la Excéntrica.
Ahora queremos utilizar los cálculos numéricos, como prometimos en el Libro III Capítulo 4 (Fig. 3.2 y 3.3), para demostrar que uno también deriva las mismas cantidades desde la hipótesis del epiciclo, y dadas las mismas proporciones se mantienen [iguales] según el camino que explicamos.
[Ver Fig. 3.11] Sea ABG el círculo concéntrico con la eclíptica, con centro en D y diámetro ADG, y el círculo del epiciclo EZH con centro en A. Desde D dibujar una tangente hasta el epiciclo, DZB, y unir AZ. Entonces, como antes, en el triángulo rectángulo ADZ, AD es 24 veces AZ, de modo que, en el círculo alrededor del triángulo rectángulo ADZ, AZ es, nuevamente, de 5p donde la hipotenusa AD es de 120p, y el arco sobre AZ es de 4;46º.
En consecuencia ^ ADZ = 4;46ºº donde 2 ángulos rectos = 360ºº
por lo tanto ^ ADZ = 2;23º donde 4 ángulos rectos = 360º.
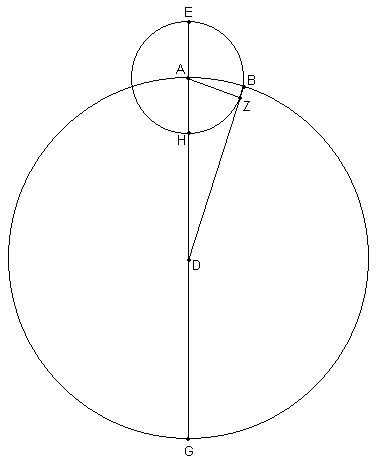
Por lo tanto, la máxima ecuación de la anomalía, a saber el arco AB, también aquí ha sido encontrada ser de 2;23º, de acuerdo con [el resultado previo], y el arco del movimiento anomalístico es de 90º, dado que esta representado por el ángulo recto AZD, mientras que el arco del movimiento medio, esta representado por el ^ EAZ, nuevamente es de 92;23º.
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Libro III |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 |
Notas de referencia
- ↑ Ver HAMA 57-8, Pedersen 144-9.
- ↑ Sobre la conveniencia en la simplicidad de las hipótesis ver el Libro III Capítulo 2 nota de referencia nro. 17.
- ↑ Leer (en los manuscritos D y Ar) en H233,1-2 en cambio de (“con cuidado”).
- ↑ De acuerdo con Ptolomeo el apogeo del Sol (no como aquellos de los cinco planetas, que más tarde se trasladan, Libro IX Capítulo 9) no involucra el movimiento de la precesión. Los reproches que se han lanzado sobre Ptolomeo (por ej. los de Manitius I 428-9) por no descubrir que el apogeo del Sol también tiene un movimiento a través de la eclíptica no están justificados. Para hacer esto Ptolomeo podría haber necesitado observaciones mucho más precisas en el instante del equinoccio y del solsticio que aquellas disponibles ([con una precisión] al más próximo ¼ de día), y no solo para su propia época sino también para una más antigua. Ver los papeles de Rome [3] y los de Petersen Viggo M. y Olaf Schmidt para una demostración matemática de ello.
- ↑ En el Libro III Capítulo 2 los instantes precisos del día dado son: “1 hora después de la salida”, “1 hora después del mediodía” y “2 horas después de la medianoche”. Por lo tanto los intervalos precisos son de 178 ¼ días y de 94 días 13 horas, principalmente en los valores corregidos de 94 días 13 horas y de 92 días 11 horas para los intervalos utilizados en los cálculos. Pero ver en el Libro III Capítulo 2 nota de referencia nro. 23, por la posibilidad de que el tiempo del solsticio ocurra en las “2 horas de estación” (≈ 1 ⅔ de horas equinocciales). Incluso un cambio tan pequeño como el de una hora en un intervalo tiene un efecto de alrededor de 1º en la ubicación del apogeo (cf. Petersen Viggo M. y Olaf Schmidtb 80-3 y en Rome [3 13-15]).
- ↑ Leer (en los manuscritos D y Ar.) en cambio de (“segmento”) en H239,12.
