Almagesto: Libro III - Capítulo 04
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
{Sobre la Hipótesis del Movimiento Circular Uniforme}
Nuestra próxima tarea es demostrar la Anomalía Aparente del Sol. Pero primero debemos dedicarnos al punto general de que los desplazamientos hacia atrás de los planetas con respecto a los cielos son, en todos los casos, justamente como el movimiento hacia adelante del Universo, de naturaleza uniforme y circular. Es decir, si imaginamos los cuerpos o sus círculos siendo transportados alrededor por líneas rectas [radios], en cada caso la línea recta en cuestión describe absolutamente ángulos iguales en tiempos iguales en el centro de su revolución. La irregularidad aparente [anomalía] en sus movimientos es el resultado de la posición y el orden de cada uno de esos círculos en la esfera mediante el cual realizan sus movimientos, y en realidad no hay en esencia nada ajeno a su naturaleza eterna en el "desorden" que se supone que exhiben los fenómenos. La razón por la apariencia de la irregularidad puede ser explicada por dos hipótesis, que son las más básicas y sencillas. Cuando sus movimientos son observados con respecto a un círculo imaginado estar en el plano de la Eclíptica, cuyo centro coincide con el centro del Universo (por lo tanto su centro puede ser considerado coincidir con nuestro punto de vista), entonces podemos suponer, tanto que el Movimiento Uniforme de cada [cuerpo] toma lugar sobre un círculo que no es concéntrico con el [del] Universo, o que tienen un círculo concéntrico, aunque toman lugar sus movimientos uniformes, no realmente sobre este círculo, sino sobre otro círculo, que es transportado por el primer círculo, y [por lo tanto] es conocido como Epiciclo. Serán demostradas que ambas de éstas hipótesis permitirán [a los planetas], parecer ante nuestros ojos, atravesar arcos desiguales de la eclíptica (que es concéntrica al Universo) en tiempos iguales.

En la Hipótesis de la Excéntrica: [ver Fig. 3.1.] imaginamos el círculo excéntrico ABGD, sobre el cuál el cuerpo lo recorre con un movimiento uniforme, con centro en E, con un diámetro AED, sobre el cual el punto Z representa el observador [2]. Por lo tanto A es el apogeo, y D el perigeo. Cortamos arcos iguales AB y DG, y unimos BE, BZ, GE y GZ. Entonces, es inmediatamente obvio que el cuerpo recorrerá los arcos AB y GD en tiempos iguales, pero [en el transcurso de su recorrido] parecerán haber atravesado arcos desiguales de un círculo dibujado sobre el centro Z. Entonces
^ BEA = ^ GED.
Pero ^ BZA < ^ BEA (o ^ GED),
y ^ GZD = ^ GED (o ^ BEA).
En la Hipótesis del Epiciclo: imaginamos [ver Fig. 3.2] el círculo ABGD concéntrico con la eclíptica con centro en E, de diámetro AEG, y el epiciclo ZHΘK transportado por él, sobre el cual el cuerpo se mueve, con centro en A.

Entonces aquí también es inmediatamente obvio que, como el epiciclo atraviesa el círculo ABGD con un movimiento uniforme, por decir, desde A hacia B, y como el cuerpo recorre el epiciclo con un movimiento uniforme, entonces cuando el cuerpo esta en los puntos Z y Θ, parecerá coincidir con A, el centro del epiciclo, pero cuando esta en otros puntos no [parecerá coincidir con A]. Entonces, cuando está, por ej. en H, su movimiento parecerá mayor que el movimiento uniforme [del epiciclo] por el arco AH, y similarmente cuando esta en K su movimiento parecerá menor que el uniforme por el arco AK.
Ahora, en este tipo de Hipótesis de la Excéntrica [3] la menor velocidad siempre ocurre en el apogeo y la mayor en el perigeo, ya que el ^ AZB [en Fig. 3.1] es siempre menor que el ^ DZG. Pero en la Hipótesis Epicíclica ambas esta y la contraria son posibles. El movimiento del epiciclo es hacia atrás con respecto a los cielos, a saber desde A hacia B (en Fig. 3.2). Ahora si el movimiento del cuerpo sobre el epiciclo es tal que este también se mueve hacia atrás desde el apogeo, es decir desde Z hacia H, la mayor velocidad ocurrirá en el apogeo, dado que sobre este punto ambos el epiciclo y el cuerpo se están moviendo en la misma dirección. Pero si el movimiento del cuerpo desde el apogeo es hacia adelante sobre el epiciclo, esto es desde Z hacia K, entonces la contraria ocurrirá: la menor velocidad ocurrirá en el apogeo, ya que en este punto el cuerpo se esta moviendo en dirección opuesta al epiciclo.
Habiendo establecido esto, seguidamente debemos realizar el punto adicional preliminar para que los cuerpos que exhiben una doble anomalía, ambas hipótesis de arriba puedan ser combinadas, tal como probaremos en nuestras discusiones [sobre] tales cuerpos, aunque para un cuerpo que visualice una única anomalía invariable, será suficiente una sola hipótesis de las anteriormente [explicadas]; y [en este caso] todo el fenómeno estará representado, sin diferencia, por ambas hipótesis, proveyendo que las mismas proporciones son preservadas en ambas [hipótesis]. Por esto me refiero que la proporción, en la Hipótesis de la Excéntrica, de la distancia entre el centro de visión y el centro de la excéntrica sobre el radio de la excéntrica, debe ser la misma como la proporción, en la Hipótesis de Epiciclo, del radio del epiciclo sobre el radio de la Deferente [4]; y además que el tiempo que toma el cuerpo, viajando hacia atrás, en recorrer la inamovible excéntrica, debe ser el mismo como el tiempo tomado por el epiciclo, también viajando hacia atrás, en atravesar el círculo con el observador como centro [de la deferente], mientras el cuerpo se mueve con igual velocidad [angular] alrededor del epiciclo, pero de manera que su movimiento en el apogeo [del epiciclo] es hacia adelante.
Si estas condiciones son cumplidas, el fenómeno idéntico resultará desde ambas hipótesis. [Ahora] demostraremos brevemente comparando las proporciones en [forma] abstracta, y más tarde por medio de los presentes números le asignaremos a ellas la anomalía del Sol [5]. Digo entonces, primero, que en ambas hipótesis, la mayor diferencia entre el movimiento uniforme y el aparente, el Movimiento No Uniforme (que es también la posición hipotética de la velocidad media de los cuerpos) [6] ocurre cuando la distancia aparente desde el apogeo comprende un cuadrante, y que el tiempo entre la posición del apogeo y la posición de la velocidad media antes mencionada es mayor que el tiempo entre la velocidad media y el perigeo. Por lo tanto, siempre, para la Hipótesis de la Excéntrica y para la Hipótesis del Epiciclo cuando el movimiento en el apogeo es hacia adelante, el tiempo desde la menor velocidad hasta la media es mayor que el tiempo desde la velocidad media hasta la mayor; dado que en ambas hipótesis el movimiento más lento toma lugar en el apogeo. Pero [para las Hipótesis del Epiciclo] cuando el sentido de la revolución de un cuerpo es hacia atrás desde el apogeo sobre el epiciclo, lo contrario es cierto: el tiempo desde la velocidad mayor hasta la media es mayor que el tiempo desde la media hasta la menor, ya que en este caso la velocidad mayor ocurre en el apogeo.
Primero, entonces, [ver Fig. 3.3.] sea ABGD la excéntrica del cuerpo con centro en E, con diámetro AEG. Sobre este diámetro tomar el centro de la eclíptica, esto es, la posición del observador, en Z, y dibujar BZD a través de Z en ángulos rectos hasta AEG. Sean las posiciones del cuerpo B y D, entonces, obviamente, su distancia aparente desde el apogeo A es un cuadrante sobre ambos lados. Tenemos que probar que la diferencia mayor entre el movimiento medio y el anomalístico toma lugar en los puntos B y D.
Unir EB y ED.

Inmediatamente es obvio que la proporción del ^ EBZ sobre los 4 ángulos rectos [360°] es igual a la proporción del arco de la diferencia debido a la anomalía [7] sobre todo el círculo [360°]; el ^ AEB subtiende el arco del Movimiento Uniforme, y el ^ AZB subtiende el arco del Movimiento Aparente No Uniforme, y la diferencia entre ellos es el ^ EBZ.
Digo, entonces, que ningún ángulo mayor que esos dos [el ^ EBZ y el ^ EDZ] puede ser construido sobre la línea EZ en la circunferencia del círculo ABGD.
[Demostración:] Construir en los puntos Θ y K los ángulos EΘZ y EKZ, y unir ΘD, [y] KD. Entonces, dado que en cualquier triángulo, el lado mayor subtiende el ángulo mayor [8],
y ΘZ > ZD,
en consecuencia ^ ΘDZ > ^ DΘZ.
Pero ^ EDΘ = ^ EΘD, dado que EΘ = ED [un radio].
Por lo tanto, por adición, ^ EDZ (= ^ EBD) > ^ EΘZ.
Nuevamente, dado que DZ > KZ,
^ ZKD > ^ ZDK.
Pero ^ EKD = ^ EDK, dado que EK = ED.
Por lo tanto, por sustracción, ^ EDZ (= ^ EBZ) > ^ EKZ.
Por lo tanto es imposible que cualquier otro ángulo ser construido por el camino definido mayor que aquellos [ángulos] en los puntos B y D.
Simultáneamente esta probado que el arco AB, que representa el tiempo desde la menor velocidad hasta la media, excede [el arco] BG, que representa el tiempo desde la velocidad media hasta la mayor, por dos veces el arco que comprende la ecuación de la anomalía. Dado que el ^ AEB excede un ángulo recto (el ^ EZB) por el ^ EBZ, y el ^ BEG poco menos que un ángulo recto por la misma cantidad.
Nuevamente, probar el mismo teorema para las otras hipótesis, sea [Fig. 3.4] el círculo ABG concéntrico con el Universo, con centro en D y de diámetro ADB, y sea el epiciclo EZH en el centro A, transportado alrededor de aquel [círculo ABG] sobre el mismo plano. Supongamos el cuerpo estar en H cuando su distancia aparente desde el apogeo es [igual a] un cuadrante. Unir AH y DHG.
Y digo que DHG es tangente al epiciclo; porque esta es la posición en la que la diferencia entre el movimiento uniforme y el anomalístico es mayor.
[Demostración:] El movimiento medio, contado desde el apogeo, esta representado por el ^ EAH; el cuerpo atraviesa el epiciclo con la misma velocidad [angular] tal como el epiciclo recorre el círculo ABG. Además la diferencia entre el movimiento medio y el movimiento aparente esta representada por el ^ ADH. Por lo tanto esta claro que la cantidad por la que el ^ EAH excede al ^ ADH (a saber el ^ AHD) representa la distancia aparente del cuerpo desde el apogeo. Aunque esta distancia es, por hipótesis, un cuadrante. Por lo tanto el ^ AHD es un ángulo recto, y en consecuencia la línea DHG es tangente al epiciclo EZH. Por consiguiente el arco AG es la diferencia mayor posible debido a la anomalía, dado que este comprende la distancia entre el centro A y la tangente.

Por el mismo razonamiento, el arco EH, que de acuerdo con el sentido de la rotación sobre el epiciclo aquí asumido, representa el tiempo de la velocidad menor hasta la media, excediendo el arco HZ, el cual representa el tiempo de la velocidad media hasta la mayor, por dos veces el arco AG. Si prolongamos DH hasta Θ y dibujamos AKΘ a ángulos rectos a EZ,
Y el arco EKH es mayor que un cuadrante por el arco KH,
mientras el arco ZH es menor que un cuadrante por el arco KH.
Lo que se ha requerido para examinar.
También es válido que los mismos efectos serán generados por ambas hipótesis si uno toma un movimiento parcial sobre la misma extensión de tiempo para ambas, si uno considera el movimiento medio o el aparente, o la diferencia entre ellos, es decir la Ecuación de la Anomalía. El mejor camino para ver esto es el siguiente.
[Ver Fig. 3.5.] [11] Sea el círculo ABG con centro en D, concéntrico con la eclíptica, y sea el círculo EZH con centro en Θ que es excéntrico pero igual a la concéntrica ABG. Sea el diámetro en común a través de sus centros D y Θ y el apogeo E en EAΘD. Cortar al azar un arco AB sobre la concéntrica, y dibujar el epiciclo KZ con centro en B y radio DΘ. Unir KBD.

Digo que el cuerpo será transportado por ambos tipos de movimientos [por ej. de acuerdo a ambas hipótesis] hasta el punto Z, la intersección de la excéntrica y del epiciclo, en el mismo instante en todos los casos (es decir, los tres arcos, el EZ sobre la excéntrica, el AB sobre la concéntrica, y el KZ sobre el epiciclo, son todos similares), y que la diferencia entre los movimientos uniformes y anomalísticos, y las posiciones aparentes del cuerpo, llegarán a ser únicas y las mismas de acuerdo con ambas hipótesis.
[Demostración:] Unir ZΘ, BZ y DZ.
Dado que, en el cuadrilátero BDΘZ, los lados opuestos son iguales, ZΘ hasta BD y BZ hasta DΘ,
BDΘZ es un paralelogramo.
Por lo tanto ^ EΘZ = ^ ADB = ^ ZBK.
Por lo tanto, ya que ellos son ángulos en los centros [de los círculos], los arcos subtendidos por ellos son también similares, por ej.
arco EZ de la excéntrica || arco AB de la concéntrica || arco KZ del epiciclo.
Por lo tanto el cuerpo será transportado en el mismo instante por ambos tipos de movimientos hasta el mismo punto, Z, y parecerá haber atravesado el mismo arco AL de la eclíptica desde el apogeo, y por consiguiente la ecuación de la anomalía será la misma en ambas hipótesis; demostramos que esta ecuación esta representada por el ^ DZΘ en la Hipótesis de la Excéntrica y por el ^ BDZ en la Hipótesis del Epiciclo, y esos dos ángulos son alternos e iguales, dado que, como hemos demostrado, ZΘ es paralela a BD.
Es obvio que los mismos resultados se mantendrán bien para todas las distancias [del cuerpo desde el apogeo]. ya que el cuadrilátero ΘDZB siempre será un paralelogramo, y [por lo tanto] el movimiento del cuerpo sobre el epiciclo actualmente [en ese instante] describirá el círculo excéntrico, siempre que las proporciones [12] sean similares y sus miembros iguales en ambas hipótesis.
Además, incluso si los miembros son distintos en tamaño, siempre que sus proporciones sean similares, el fenómeno resultará el mismo. Esto puede ser demostrado del siguiente modo.
Como antes [ver Fig. 3.6] sea ABG el círculo concéntrico con el Universo con centro en D y el diámetro ADG, sobre el cual el cuerpo alcanza la posición del apogeo y del perigeo. Sea el epiciclo dibujado sobre el punto B, a una distancia arbitraria, [y] el arco AB desde el apogeo A. Sea el arco EZ atravesado por el cuerpo [sobre el epiciclo], que es, obviamente, similar a AB, dado que las revoluciones sobre [ambos] círculos tienen el mismo período. Unir DBE, BZ, DZ.

Ahora, es inmediatamente obvio que, de acuerdo con estas hipótesis [de los epiciclos], el ^ ADE será siempre igual al ^ ZBE, y el cuerpo parecerá ubicarse sobre la línea DZ.
Pero digo que el cuerpo también parecerá ubicarse sobre la misma línea DZ de acuerdo con la hipótesis de la excéntrica, si la excéntrica es mayor o menor que la concéntrica ABG, siempre que uno suponga que las proporciones son similares y que los períodos de revolución son los mismos.
[Demostración:] Sea la excéntrica HΘ con centro en K ([el cuál debe ubicarse] sobre AG), dibujada bajo las condiciones que hemos descrito, mayor [que la concéntrica ABG], y LM con centro en N (este también [debe ubicarse sobre AG]), más pequeña [que la concéntrica ABG].
Prolongar DZ como DMZΘ, y DA como DLAH, y unir ΘK y [// a] MN.
Entonces dado que
DB / BZ = ΘK / KD = MN / ND [por hipótesis],
y ^ BZD = ^ MDN (ya que DA es paralela a BZ);
los tres triángulos [ZDB, DΘK, DMN] son iguales en sus ángulos,
y ^ BDZ = ^ DΘK = ^ DMN (son ángulos subtendidos por lados correspondientes).
Por lo tanto DB, ΘK y MN son paralelos.
En consecuencia ^ ADB = ^ AKΘ = ^ ANM.
Y dado que esos ángulos están en los centros de sus [respectivos] círculos, también los arcos AB, HΘ y LM sobre ellos serán similares.
Entonces es cierto, no solo que el epiciclo ha atravesado el arco AB en el mismo tiempo como el cuerpo ha atravesado el arco EZ, sino que también el cuerpo ha recorrido los arcos HΘ y LM sobre las excéntricas en ese mismo tiempo; por lo tanto en cada caso [el cuerpo] será visto a lo largo de la misma línea DMZΘ, de acuerdo con la [hipótesis] del epiciclo en el punto Z, de acuerdo a la excéntrica más grande sobre el punto Θ, y de acuerdo con la excéntrica más pequeña sobre el punto M. Lo mismo se mantendrá válido en todas las posiciones.
Una futura consecuencia es aquella donde la distancia aparente del cuerpo desde el apogeo [en un momento dado] es igual a su distancia aparente desde el perigeo [sobre otro], la ecuación de la anomalía será la misma en ambas posiciones.
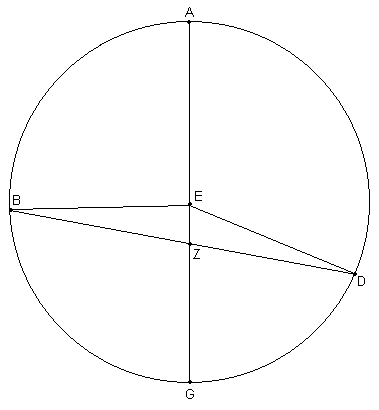
[Demostración:] En la hipótesis de la excéntrica [ver Fig. 3.7], dibujamos un círculo excéntrico ABGD con centro en E y diámetro AEG a través del apogeo A. Supongamos que el observador esta ubicado en Z, y dibujamos una [cuerda] arbitraria BZD a través de Z, y unir EB y ED. Entonces las posiciones aparentes [del cuerpo en B y D] serán iguales y opuestas, esto es, el ángulo AZB desde el apogeo será igual y opuesto al ángulo GZD desde el perigeo; y la Ecuación de la Anomalía será la misma [en ambos casos], dado que
dado que BE = ED, y ^ EBZ = ^ EDZ.
Entonces el arco [AB] del movimiento medio contado desde el apogeo A excederá al arco del movimiento aparente (por ej. el arco subtendido por el ángulo AZB) por la misma ecuación [igual al ^ EBZ] tal como el arco del movimiento medio contado desde el perigeo G es excedido por el arco del movimiento aparente (por ej. el arco [igual] subtendido por el ^ GZD). Dado que
^ AEB > ^ AZB, y ^ GED < ^ GZD.

En la Hipótesis del Epiciclo [ver Fig. 3.8] si, como antes, dibujamos la concéntrica ABG con centro en D y diámetro ADG, y el epiciclo EZH con centro en A, dibujamos una línea arbitraria DHBZ, y unimos AZ y AH, entonces el arco AB representando la Ecuación de la Anomalía que será la misma en ambas posiciones, por ej. si el cuerpo esta en Z o en H. Y la distancia del cuerpo desde el punto sobre la eclíptica correspondiente al apogeo cuando este esta en Z será igual a su distancia desde el punto correspondiente hasta el perigeo cuando este esta en H. Ya que el arco de su distancia aparente desde el apogeo esta representado por el ^ DZA, dado que, como demostramos, esta es la diferencia entre el movimiento medio y la ecuación de la anomalía [13]. Y el arco de su distancia aparente desde el perigeo esta representado por el ^ ZHA (dado que esto, también, es igual al movimiento medio desde el perigeo más la ecuación de la anomalía).
Pero ^ DZA = ^ ZHA, ya que AZ = AH.
Por lo tanto aquí también concluimos que el movimiento medio excede al aparente cerca del apogeo (por ej. el ^ EAZ excede al ^ AZD) por la misma ecuación (a saber el ^ ADH) como el movimiento medio es excedido por el (mismo) movimiento aparente (por ej. el ^ HAD por el ^ AHZ) cerca del perigeo.
Lo que se ha requerido para examinar.
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Libro III |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 |
Notas de referencia
- ↑ Ver HAMA 55-7, Pedersen 134-44.
- ↑ “el observador”; literalmente “nuestro punto de vista”.
- ↑ Ptolomeo esta insinuando sobre la existencia de otro tipo de Hipótesis de las Excéntrica, una de las cuales es geométricamente equivalente a la Hipótesis del Epiciclo en la que el sentido de rotación es el mismo para ambos: planeta y epiciclo. Aunque [Ptolomeo] no discute esto hasta el Libro XII Capítulo 1, donde aprendemos que tal equivalencia ya era conocida por Apolonio de Perge (c. 200 a. C.). Ver HAMA 149-50.
- ↑ “deferente”: ver Introducción.
- ↑ Referencia en este Libro III Capítulo 4, Fig. 3.11.
- ↑ Ptolomeo nunca considera [necesario] probar este enunciado acerca de la posición donde el movimiento aparente es igual al movimiento medio, aunque intuitivamente es visto como válido en el modelo del epiciclo. Ver HAMA 57, Pedersen 143.
- ↑ Esta expresión es utilizada mas tarde aquí como un término técnico para el ángulo EBZ correspondiente, y usualmente es traducido como la “Ecuación de la Anomalía”. Ver la Introducción.
- ↑ Precisamente esta declaración, de que el ángulo mayor es subtendido por el lado mayor, es el enunciado de Euclides I 19 (que Heiberg se refiere ad loc.). Pero de hecho lo que sostiene la declaración de Ptolomeo es que, si el lado a es mayor al lado b, el ángulo A es mayor que el ángulo B [explicado] por Euclides I 18. Quizás deberíamos adoptar la lectura del manuscrito D, (“el ángulo mayor subtiende el lado mayor”, y asume que el texto ha sido asimilado por la redacción (errónea) Euclidiana.
- ↑ Euclides VI 8.
- ↑ Para obtener un texto gramatical he borrado en H225,4. Este fue introducido (en un período más temprano, dado que es reflejado en las traducciones Árabes) como una corrección de la declaración imprecisa de Ptolomeo (para la mente escolástica) de que el arco KH es igual al arco AG. Ya que los arcos están sobre los círculos de diferentes tamaños, técnicamente ellos son solamente “similares”. Una corrección alternativa podría ser (que se encuentra actualmente en el comentario de Teón ad loc., Roma III 868,8, aunque probablemente sea una parafrase, que también parece estar detrás del manuscrito L).
- ↑ La figura en Heiberg (p. 225) omite erróneamente la letra correspondiente al manuscrito L (aunque esto es hallado a través de todos los manuscritos). Manitius, engañado por esto, "enmienda” ΑΛ en H226,23 sobre los extravagantes 'AB'.
- ↑ Las proporciones son e/R y r/R.
- ↑ ^ DZA = ^ EAZ - ^ ADZ, demostrado en la página Fig. 3.3.
