Almagesto: Libro IV - Capítulo 06
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
{Demostración de la primera Anomalía simple de la Luna}
Que lo anterior nos sea suficiente como una teoría preliminar. Para la razón mencionada, ahora demostraremos la anomalía lunar en cuestión por medio de la Hipótesis del Epiciclo. [Para tal propósito] utilizaremos, primero, de entre los eclipses más antiguos disponibles para nosotros, tres [de los cuales hemos seleccionado] como grabados de manera inequívoca, y, segundo, [repetiremos el procedimiento] utilizando, de entre los eclipses contemporáneos, tres que hemos observado nosotros mismos con mucha precisión. En este sentido nuestros resultados serán válidos sobre un largo período como fuese posible, y en particular será aparente que aproximadamente la misma Ecuación [Máxima] de la Anomalía resulte de ambas demostraciones, y que el incremento en los movimientos medios [entre los dos conjuntos de eclipses] concuerda [2] con aquel calculado a partir de los períodos anteriores (corregidos por nosotros).
A los propósitos de demostrar la primera anomalía, considerada separadamente, la hipótesis del epiciclo que [hemos] mencionado puede ser descrita seguidamente. Imaginar un círculo en la esfera de la Luna siendo concéntrico a y se ubica en el mismo plano como el de la Eclíptica. Inclinado a ésta, en un ángulo correspondiente a la cantidad de su [máxima] desviación en latitud, hay otro círculo, que se mueve uniformemente hacia adelante (con respecto al centro de la eclíptica) con una velocidad igual a la diferencia entre los movimientos en latitud y longitud. Sobre este círculo inclinado suponemos el llamado “Epiciclo” a ser transportado, con un Movimiento Uniforme, hacia atrás con respecto de los cielos, correspondiendo al movimiento en latitud. (Este movimiento, obviamente, representará el movimiento [medio] en longitud con respecto a la eclíptica). Sobre el mismo epiciclo [suponemos que] la Luna [se] mueve, en tal sentido que sobre el arco cerca del apogeo su movimiento es hacia adelante con respecto de los cielos, con una velocidad correspondiente al período de una revolución en anomalía. No obstante, a los propósitos de la presente demostración no sufriremos consecuencias negativas si descuidamos el movimiento hacia adelante en latitud y la inclinación de la órbita de la Luna, dado que tal pequeña inclinación no tiene un efecto notable sobre la posición en longitud [3].
Primero, los tres Eclipses más antiguos seleccionados son aquellos observados en Babilonia.
El primero es el registrado ocurriendo en el primer año de Mardokempad, 29/30 de Thoth [I] en el calendario Egipcio [19/20 de Marzo de –720]. El eclipse comienza, dice, más de una hora después de la salida de la Luna, y fue total [4].
Ahora dado que el Sol estuvo cerca del final de Pisces, y [por lo tanto] la longitud de la noche fue alrededor de 12 horas equinocciales, el comienzo del eclipse ocurrió, claramente, 4 ½ horas equinocciales antes de la medianoche, y el eclipse medio (dado que fue Total) 2 ½ horas antes de la medianoche [5]. Ahora para todas determinaciones de tiempo tomamos como Meridiano estándar el meridiano a través de Alejandría, que esta cerca de ⅚ de una hora equinoccial antes [por ej. al Oeste] del meridiano a través de Babilonia [6]. Entonces en Alejandría el eclipse medio en cuestión ocurrió 3 ⅓ horas equinocciales antes de la medianoche, en tal hora la posición verdadera del Sol, de acuerdo con las tablas calculadas anteriormente, estuvo aproximadamente en ♓︎ 24 ½º.
El segundo eclipse es el registrado ocurriendo en el segundo año del mismo Mardokempad, 18/19 de Thoth [I] en el calendario Egipcio [8/9 de Marzo –719].
El [máximo] oscurecimiento, dice, fue de 3 dígitos [7] desde [el limbo] Sur [de la Luna] exactamente a la medianoche. Entonces, dado que el eclipse medio fue exactamente a la medianoche en Babilonia, debe haber ocurrido ⅚ horas antes de la medianoche en Alejandría, en tal instante la posición verdadera del Sol estuvo en ♓︎ 13 ¾º.
El tercer eclipse es el registrado ocurriendo en el (mismo) segundo año de Mardokempad, 15/16 de Phamenoth [VII] en el calendario Egipcio [1/2 de Septiembre de –719]. El eclipse comienza, dice, después de la salida de la Luna, y el [máximo] oscurecimiento fue de más de la mitad [del disco lunar] desde el [limbo] Norte. Entonces, dado que el Sol estuvo cerca del principio de Virgo, la longitud de la noche en Babilonia fue alrededor de 11 horas equinocciales, y la mitad de la noche ocurrió a 5 ½ horas [equinocciales]. Por lo tanto el comienzo del eclipse fue alrededor de 5 horas equinocciales antes de la medianoche (ya que este comienza después de la salida de la Luna), y el eclipse medio cerca de 3 ½ horas antes de la medianoche (dado que el tiempo total de un Eclipse de este tamaño debe haber sido de alrededor de 3 horas) [8]. Entonces en Alejandría el eclipse medio ocurrió 4 ⅓ horas equinocciales antes de la medianoche, en tal instante la posición verdadera del Sol estuvo cerca de ♍︎ 3 ¼º.
Entonces, es claro que el movimiento del Sol (el cual es el mismo como el de la Luna aparte de las revoluciones completas) es
| desde la mitad del primer eclipse hasta la mitad del segundo: de 349;15º |
| desde la mitad del segundo eclipse hasta la mitad del tercero: de 169;30º |
Los intervalos de tiempo son:
| desde el primero hasta el segundo: 354 días 2 ½ hs. contados simplemente |
| desde el primero hasta el segundo: 345 días 2 17/30 hs. contados en días solares medios |
| desde el segundo hasta el tercero: 176 días 20 ½ hs. contados simplemente |
| desde el segundo hasta el tercero: 176 días 20 ⅕ hs. contados en días solares medios |
Sobre tales pequeños intervalos no habrá una diferencia apreciable si uno utiliza períodos aproximados [para determinar los movimientos medios de la Luna] [9]. Los movimientos medios de la Luna son, luego, (por más de una revolución completa), aproximadamente
| en 354 días 2 17/30 hs. | 306;25º en anomalía |
| en 354 días 2 17/30 hs. | 345;51º en longitud |
| en 176 días 20 ⅕ hs. | 150;26º en anomalía |
| en 176 días 20 ⅕ hs. | 170;7º en longitud |
Así es claro que el movimiento sobre el epiciclo de 306;25º sobre el primer intervalo ha producido un incremento de [349;15º - 345;51º =] 3;24º el movimiento medio, y el movimiento [en el epiciclo] de 150;26º en el segundo intervalo ha producido una disminución del movimiento medio de [169;30º - 170;7º =] 0;37º.
Con lo de arriba como dato, sea ABG [el círculo, Fig. 4.4.] del epiciclo de la Luna, sobre el cual el punto A es la ubicación de la Luna en la mitad del primer eclipse, B su posición en la mitad del segundo eclipse, y G su posición en la mitad del tercer eclipse.
Debemos imaginar la Luna moviéndose sobre el epiciclo desde B hasta A y desde A hasta G en tal sentido que el arco AGB, cuyo incremento en movimiento entre el primer y segundo eclipse, es de 306;25º y produce un incremento de 3;24º sobre el movimiento medio, mientras el arco BAG, cuyo incremento en movimiento entre el segundo y tercer eclipse, es de 150;26º, y produce una disminución de 0;37º en el movimiento medio. Por lo tanto el movimiento desde B hasta A es de 53;35º y produce una disminución de 3;24º en el movimiento medio, y el movimiento desde A hasta G es de 96;51º y produce un incremento de 2;47º sobre el movimiento medio.
Ahora el perigeo del epiciclo no puede ubicarse sobre el arco BAG. Esto es claro ya que este arco tiene un efecto sustractivo, y es menor que un semicírculo, mientras la mayor velocidad ocurre en el perigeo. Entonces, dado que, [el perigeo] necesariamente se ubica en el arco GEB [10], tomemos el centro de la eclíptica, que es también el centro de la deferente, como el punto D, y dibujemos las líneas DA, DEB y DG hasta los puntos que representan [las posiciones de la Luna en] los tres eclipses. Con el fin de hacer la secuencia de la prueba fácilmente transferible para los cálculos de este tipo, si utilizamos la Hipótesis del Epiciclo (como [lo haremos] ahora) en nuestras demostraciones, o la Hipótesis de la Excéntrica [ver Fig. 4.5.], en tal caso el centro D es tomado dentro del círculo, damos la siguiente descripción generalmente aplicable.
Prolongar una de las tres líneas rectas dibujadas [DA, DB, DG] hasta la circunferencia opuesta (en este caso ya tenemos DEB dibujada hasta E desde el punto B del segundo eclipse), y dibujar una línea uniendo los puntos de los otros dos eclipses (aquí AG). Desde el punto donde la primer línea prolongada corta la circunferencia (aquí E), nuevamente dibujar [dos] líneas hasta los otros dos puntos (aquí EA, EG), y [desde el mismo punto] eliminar las perpendiculares a las líneas entre los otros dos puntos y el centro de la eclíptica (aquí EZ hacia AD y EH hacia GD). Desde uno de esos dos puntos (aquí G) eliminar una perpendicular a la línea dibujada desde la otra (aquí A) hasta la intersección extra [con la circunferencia] (aquí E) resultante de [la primer línea recta, DB,] siendo prolongada (en ese caso, eliminamos GΘ hacia AE). En cualquier punto comenzamos a dibujar la figura, encontraremos que las mismas proporciones resultan de los números utilizados en la demostración. Nuestra elección [del punto de partida] es guiada simplemente por conveniencia.
Entonces, dado que encontramos que el arco BA subtiende 3;24º de la eclíptica,
el ángulo en su centro, ^ BDA = 3;24º donde 4 ángulos rectos = 360º
el ángulo en su centro, ^ BDA = 6;48º donde 2 ángulos rectos = 360ºº.
Por lo tanto en el círculo alrededor del triángulo rectángulo DEZ.
arco EZ = 6;48º
y EZ = 7;7,0p donde la hipotenusa DE = 120p.
Similarmente, dado que el arco BA = 53;35,
el ángulo [que subtiende] en la circunferencia,
^ BEA = 53;35ºº donde 2 ángulos rectos = 360ºº.
Pero, en las mismas unidades, ^ BDA = 6;48ºº.
Por lo tanto, por sustracción, ^ EAZ = 46;47ºº en las mismas unidades.
Por lo tanto en el círculo alrededor del triángulo rectángulo AEZ,
arco EZ = 46;47º
y EZ = 47;38,30p donde la hipotenusa EA = 120p.
Por lo tanto donde EZ = 7;7,0p y ED = 120p,
AE = 17;55,32p.
Nuevamente, dado que el arco BAG subtiende 0;37º de la eclíptica,
el ángulo en su centro, ^ BDG = 0,37° donde 4 ángulos rectos = 360º
el ángulo en su centro, ^ BDG = 1;14°° donde 2 ángulos rectos = 360ºº.
Por lo tanto en el círculo alrededor del triángulo rectángulo DEH,
arco EH = 1;14º
y EH = 1;17,30p donde la hipotenusa DE = 120p.
Similarmente, dado que arco BAG = 150;26º,
el ángulo [que subtiende] en la circunferencia,
^ BEG = 150;26ºº donde 2 ángulos rectos = 360ºº.
Pero ^ BDG = 1;14ºº en las mismas unidades.
Por lo tanto, por sustracción, ^ EGD = 149;12ºº.
Por lo tanto en el círculo alrededor del triángulo rectángulo GEH,
arco EH = 149;12º
y EH = 115;41,21p [11] donde la hipotenusa GE = 120p.
Por lo tanto donde EH = 1;17,30p y DE = 120p,
GE = 1;20,23p,
y, como demostramos, EA = 17;55,32p en las mismas unidades.
Nuevamente dado que, como demostramos,
arco AG = 96;51º,
El ángulo [subtendido] en la circunferencia,
^ AEG = 96;51ºº donde 2 ángulos rectos = 360ºº.
Por lo tanto en el círculo alrededor del triángulo rectángulo GEΘ,
arco GΘ = 96;51º
y arco EΘ = 83;9º (complementario).
Entonces las cuerdas correspondientes
GΘ = 89;46,14p (*)
y EΘ = 79;37,55p (*)
(*) donde la hipotenusa GE = 120p.
Por lo tanto donde GE = 1;20,23p
GΘ = 1;0,8p
y EΘ = 0;53,21p.
Y, en las mismas unidades, toda la línea EA fue hallada ser de de 17;55,32p. Por lo tanto, por sustracción, ΘA = 17;2,11p donde GΘ = 1;0,8p.
Y el cuadrado en AΘ es de 290;14,19
mientras que el cuadrado en GΘ es de 1;0,17.
Pero AG² = AΘ² + GΘ² = 291;14,36.
Por lo tanto AG = 17;3,57p donde DE = 120p y GE = 1;20,23p.
Pero, donde el diámetro del epiciclo es de 120p,
AG = 89;46,14p (dado que subtiende el arco AG, que es de 96;51º).
Por lo tanto donde AG = 89;46,14p
y el diámetro del epiciclo es de 120p,
DE = 631;13,48p
y GE = 7;2,50p.
Por lo tanto el arco GE del epiciclo = 6;44,1º.
Y, por hipótesis, el arco BAG = 150;26º.
Por lo tanto, por adición,
el arco BGE = 157;10,1º,
entonces su cuerda, BE = 117;37,32p
donde el diámetro del epiciclo es de 120p
y ED = 631;13,48p.
Ahora, si hemos encontrado BE igual al diámetro del epiciclo, el centro del epiciclo podría, obviamente, ubicarse en él, e inmediatamente podríamos tomar la proporción entre los diámetros [del epiciclo y la deferente]. Sin embargo, dado que esta es menor que el diámetro, y también el arco BGE es menor que un semicírculo, es claro que el centro del epiciclo caerá fuera del segmento [(arco)] BAGE.
Sea este [el centro del epiciclo] en el punto K [Fig. 4.6], y dibujar la línea DMKL desde D, el centro de la eclíptica, a través de K. Por lo tanto el punto L representa el apogeo del epiciclo y M su perigeo. Entonces
BD * DE = LD * DM [12];
y hemos demostrado que donde el diámetro LKM = 120p,
BE = 117;37,32p y ED = 631;13,48p.
Por lo tanto, por adición, BD = 748;51,20p.
Por lo tanto LD * DM = BD * DE = 472700;5,32p.
Además, dado que LD * DM + KM² = DK² [13]
y el radio del epiciclo, KM = 60p,
KM² = 3600p,
y DK² = 472700;5,32p + 3600p = 476300;5,32p.
Por lo tanto DK, [que es] el radio de la deferente círculo concéntrico a la eclíptica, es de 690;8,42p donde KM, el radio del epiciclo, es de 60p.
Entonces, donde el radio de la deferente, cuyo centro coincide con el observador, es de 60p, el radio del epiciclo es alrededor de 5;13p.
Repitiendo la misma figura [Fig. 4.7], eliminar la perpendicular KNX desde el centro K hasta BE, y unir BK.
Ahora, donde DK = 690;8,42p,
encontramos que DE = 631;13,48p
y NE = ½ BE = 58;48,46p.
Por lo tanto, por adición, DEN = 690;2,34p.
Por lo tanto en el círculo alrededor del triángulo rectángulo DNK,
DN = 119;58,57p donde la hipotenusa DK = 120p,
y arco DN ≈ 178;2º.
Por lo tanto ^ DKN = 178;2ºº donde 2 ángulos rectos = 360ºº
en consecuencia ^ DKN = 89;1º donde 4 ángulos rectos = 360º.
Por lo tanto el arco XM del epiciclo = 89;1º,
y arco LBX = 90;59º (complementario),
y arco XB = ½ * arco BXE = 78;35º (dado que el arco BE fue determinado alrededor de 157;10º [Fig. 4.6]).
Por lo tanto, por substracción, el arco LB del epiciclo es de 12,24º, que es la distancia de la Luna desde el apogeo del epiciclo en la mitad del segundo eclipse en cuestión.
Similarmente, dado que, como hemos demostrado,
^ DKN = 89;1º donde 4 ángulos rectos = 360º,
por substracción, el ^ KDN es de 0;59º (complementario del ^ DKN) que representa la Ecuación de la Anomalía (que es sustractiva [(negativa)] respecto al movimiento medio) correspondiente al arco LB del epiciclo. Por lo tanto la posición media de la Luna en la mitad del segundo eclipse fue en ♍︎ 14;44º, dado que su verdadera posición estuvo en ♍︎ 13;45º, correspondiente a la posición del Sol en Pisces.
Volvamos ahora a los tres eclipses que hemos seleccionado de aquellos observados por nosotros muy cuidadosamente en Alejandría.
El primero ocurrió en el decimoséptimo año de Adriano, 20/21 de Pauni [X] en el calendario Egipcio [6/7 de Mayo de 133]. Calculamos el tiempo exacto del eclipse medio como de ¾ de una hora equinoccial antes de la medianoche. Fue total [14]. En aquel tiempo la posición verdadera del Sol estuvo alrededor de ♉︎ 13 ¼º.
El segundo ocurrió en el decimonoveno año de Adriano, 2/3 de Choiak [IV] en el calendario egipcio [20/21 de Octubre del 134]. Calculamos que el eclipse medio ha ocurrido 1 hora equinoccial antes de la medianoche. [La Luna] fue eclipsada ⅚ de su diámetro desde el Norte [15]. En aquella hora la verdadera posición del Sol estuvo en ♎︎ 25 ⅙º.
El tercer eclipse ocurrió en el vigésimo año de Adriano, 19/20 de Pharmouthi [VII] en el calendario Egipcio [5/6 de Marzo de 136]. Calculamos que el eclipse medio ocurrió 4 horas equinocciales después de la medianoche. [La Luna] fue eclipsada mitad de su diámetro desde el [limbo] Norte [16]. En aquel tiempo la posición del Sol estuvo alrededor de ♓︎ 14 1/12º.
Esta claro aquí también que el movimiento medio [en longitud] de la Luna, más allá de una revolución completa, es igual a aquel del Sol, y es:
| desde la mitad del primer eclipse hasta la mitad del segundo: 161;55º |
| desde la mitad del segundo eclipse hasta la mitad del tercero: 138;55º |
La longitud del primer intervalo es de:
| 1 año Egipcio de 166 días 23 ¾ horas equinocciales recontadas simplemente |
| 1 año Egipcio de 166 días 23 5/8 horas equinocciales recontadas en forma precisa |
La longitud del segundo intervalo es de:
| 1 año Egipcio de 137 días 5 horas equinocciales recontadas simplemente |
| 1 año Egipcio de 137 días 5 ½ horas equinocciales recontadas en forma precisa |
El movimiento medio aproximado de la Luna (más allá de una revolución completa) es:
| en 1 año 166 días 23 5/8 hs. | de 110;21º en anomalía |
| en 1 año 166 días 23 5/8 hs. | de 169;37º en longitud |
| y en 1 año 137 días 5 ½ hs. | de 81;36º en anomalía |
| y en 1 año 137 días 5 ½ hs. | de 137;34º en longitud |
Por lo tanto, claramente, los 110;21º del movimiento en el epiciclo sobre el primer intervalo ha producido una disminución en el movimiento medio de [161;55º - 169;37º =] 7;42º, mientras los 81;36º de movimiento en el epiciclo sobre el segundo intervalo ha producido un incremento en el movimiento medio de [138;55º - 137;34º =] 1;21º.
Con los datos de arriba, [Fig. 4.8] sea ABG el epiciclo de la Luna. Sea A el punto en el cual la Luna estuvo en la mitad del primer Eclipse, B su ubicación en la mitad del segundo eclipse, y G su posición en la mitad del tercero.
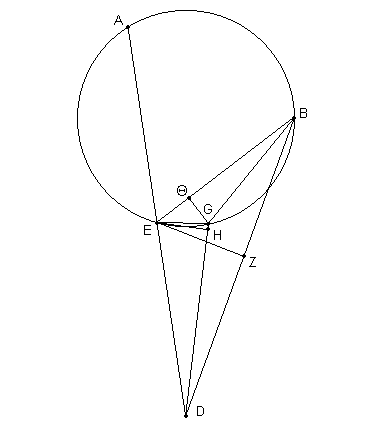
Nuevamente debemos imaginar el movimiento de la Luna tomando lugar desde A hasta B y luego desde B hasta G en tal sentido que, como dijimos, el arco AB, que es de 110;21º, produce una disminución de 7;42º con respecto al movimiento medio, mientras el arco BG, que es de 81;36º, produce un incremento de 1;21º con respecto al movimiento medio; por lo tanto el arco remanente GA es de 168;3º y produce un incremento al movimiento medio de 6;21º, que es la diferencia [entre 7;42º y 1;21º].
Es claro que el apogeo debe ubicarse en el arco AB, dado que este no puede [hacerlo] tanto en el arco BG o en el arco GA, ambos de los cuales producen un efecto aditivo y son menores que un semicírculo. En el mismo sentido [como antes] [17], tomar D como el centro de la eclíptica y el círculo transportando el Epiciclo, y dibujar desde él, hasta los puntos representando los tres eclipses, las líneas DEA, DB, DG. Unir BG y dibujar desde el punto E hasta el [punto] B y G las líneas EB y EG, y eliminar hasta las líneas BD y DG las perpendiculares EZ y EH. También eliminar la perpendicular GΘ desde G hasta BE.
Entonces, dado que el arco AB subtiende 7;42º sobre la eclíptica, el ángulo en el centro de la eclíptica,
^ ADB = 7;42º donde 4 ángulos rectos = 360º.
^ ADB = 15;24º donde 2 ángulos rectos = 360ºº.
Por lo tanto en el círculo alrededor del triángulo rectángulo [18] DEZ,
arco EZ = 15;24º
y EZ = 16;4,42p donde la hipotenusa DE = 120p.
Similarmente, dado que arco AB = 110;21º,
el ángulo [subtendido por él] en la circunferencia,
^ AEB = 110;21ºº donde 2 ángulos rectos = 360ºº.
Pero ^ ADB = 15;24ºº en las mismas unidades.
Por lo tanto, por substracción, ^ EBD = 94;57ºº
Por lo tanto, en el círculo alrededor del triángulo rectángulo [19] BEZ,
arco EZ = 94;57º
y EZ = 88;26,17p donde la hipotenusa BE = 120p.
Por lo tanto, donde EZ = 16;4,42p y DE = 120p,
BE = 21;48,59p.
Además, ya que, como demostramos, el arco GEA subtiende 6;21º de la eclíptica, el ángulo en el centro de la eclíptica también,
^ ADG = 6;21º donde 4 ángulos rectos = 360º
^ ADG = 12;42ºº donde 2 ángulos rectos = 360ºº.
Por lo tanto en el círculo alrededor del triángulo rectángulo DEH,
arco EH = 12;42º
y EH = 13;16,19p donde la hipotenusa DE = 120p.
Similarmente, dado que arco ABG = 191;57º,
el ángulo [subtendido por él] en la circunferencia,
^ AEG = 191;57ºº donde 2 ángulos rectos = 360ºº.
Pero el ^ ADG fue hallado ser de 12;42ºº en las mismas unidades.
Por lo tanto, por substracción, el ^ EGD = 179;15ºº en las mismas unidades.
Por lo tanto, en el círculo alrededor del triángulo rectángulo GEH,
arco EH = 179;15º
y EH = 119;59,50p donde la hipotenusa GE = 120p.
Por lo tanto, donde EH = 13;16,19p y DE [20] = 120p,
GE = 13;16,20p.
Y, como demostramos, BE = 21;48,59p en las mismas unidades.
Además, dado que el arco BG = 81;36º, el ángulo [subtendido por él] en la circunferencia,
^ BEG = 81;36ºº donde 2 ángulos rectos = 360ºº.
Por lo tanto en el círculo alrededor del triángulo rectángulo GEΘ,
el arco GΘ = 81;36° y el arco EΘ = 98;24° (suplementario).
Por lo tanto las correspondientes cuerdas
GΘ = 78;24,37p donde la hipotenusa EG = 120p.
y EΘ = 90;50,22p donde la hipotenusa EG = 120p.
Por lo tanto donde GE = 13;16,20p,
GΘ = 8;40,20p y EΘ = 10;2,49p.
Y la línea completa EB fue hallada ser de 21;48,59p en las mismas unidades.
Por lo tanto por substracción [de EΘ desde EB],
ΘB = 11;46,10p donde GΘ = 8;40,20p.
Y ΘB² = 138;31,11p, GΘ² = 75;12,27p.
y BG² = ΘB² + GΘ² = 213;43,38p.
Por lo tanto BG = 14;37,10p donde DE = 120p y GE = 13;16,20p.
Pero donde el diámetro del epiciclo es de 120p,
BG = 78;24,37p (es la cuerda del arco BG, que es de 81;36º).
Por lo tanto, donde BG = 78;24,37p y el diámetro del epiciclo es de 120p.
DE = 643;36,39p y GE = 71;11,4p.
Por lo tanto arco GE del epiciclo = 72;46,10º.
Y, por hipótesis, arco GEA = 168;3º.
Por lo tanto, por sustracción, arco EA = 95;16,50º
y por lo tanto su cuerda AE = 88;40,17p
donde el diámetro del epiciclo es de 120p y donde ED = 643;36,39p.
Además, dado que el arco EA fue demostrado ser menor que un semicírculo, el centro del epiciclo se ubicará, obviamente, fuera del segmento EA. Tomar como centro el punto K [Fig. 4.9.], y dibujar la línea DMKL, es decir, nuevamente, el punto L representa el apogeo y el punto M el perigeo. Luego
AD * DE = LD * DM,
y hemos demostrado que, donde el diámetro del epiciclo LKM = 120p,
AE = 88;40,17p y ED = 643;36,39p
(por lo tanto, por adición, AD = 732;16,56p).
En consecuencia LD * DM = AD * DE = 471304;46,17.
Nuevamente, dado que
LD * DM + KM² = DK²,
y KM, el radio del epiciclo, es de 60p.
si adicionamos las 3600p (de KM²) [21] a las 471304;46,17p de arriba,
encontramos DK² = 474904;46,17p.
Por lo tanto, el radio de la deferente, concéntrica con la Eclíptica,
DK = 689;8p donde el radio del epiciclo, KM = 60p.
Por lo tanto donde la línea que une los centros de la eclíptica y del epiciclo es de 60p, el radio del epiciclo es de 5;14p.
Esta proporción (razón) es muy próxima a la misma que aquella justamente derivada anteriormente desde el más antiguo de los eclipses.
Entonces, en la misma figura [Fig. 4.10] eliminar la perpendicular KNX desde el centro K hasta DEA, y unir AK.
Entonces, como demostramos,
Donde DK = 689;8p, DE = 643;36,39p;
y NE = ½ * AE = 44;20,8p en las mismas unidades.
Por lo tanto, por adición, DEN = 687;56,47p.
Por lo tanto, donde la hipotenusa DK = 120p, DN = 119;47,36p,
y en el círculo en el triángulo rectángulo DKN,
arco DN ≈ 173;17º.
Por lo tanto DKN = 173;17ºº donde 2 ángulos rectos = 360ºº
en consecuencia DKN = 86;38,30º donde 4 ángulos rectos = 360º.
Por lo tanto arco MEX del epiciclo = 86;38,30º,
y arco LAX = 93;21,30º (suplementario),
y arco AX = ½ * arco AE ≈ 47;38,30º.
Por lo tanto, por sustracción, arco AL = 45;43º.
Pero, por hipótesis, todo el arco AB = 110;21º.
Por lo tanto, por sustracción, arco LB = 64;38º.
Esta es la distancia de la Luna desde el apogeo en la mitad del segundo eclipse determinado arriba.
Similarmente, como demostramos,
^ DKN ≈ 86;38º,
entonces ^ KDN = 3;22º (complementario),
y, por hipótesis, ^ ADB = 7;42º.
Por lo tanto, por sustracción, ^ LDB = 4;20º.
Este ángulo subtiende el arco de la eclíptica representando la Ecuación de la Anomalía (que es sustractiva [(negativa)] respecto al movimiento medio) resultando desde el arco LB del epiciclo.
Por lo tanto la posición media de la Luna en la mitad del segundo eclipse estuvo en ♈︎ 29;30º, dado que su verdadera posición estuvo en ♈︎ 25;10º, correspondiente a la posición del Sol en Libra.
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Libro IV |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 | 11 |
Notas de referencia
- ↑ Ver HAMA 73-8, Pedersen 169-79.
- ↑ Leer (en el manuscrito D, y en el Ar) en cambio de (“siempre de acuerdo”) en H301,10.
- ↑ Por ejemplo, a los propósitos del cálculo de la longitud de la órbita lunar es tratada como si ella se ubicara en el plano de la eclíptica. El máximo error resultante (para ι ≈ 5º) es alrededor de 6' (cf. HAMA 83 ). Ptolomeo mismo (Libro VI Capítulo 7) lo estima como de 5'.
- ↑ Fecha y horas calculadas con un programa de computación desde la observación realizada por los Babilonios (actual Bagdad) del siguiente:
Eclipse lunar Fecha Tipo Eclipse 1° Contacto con la Umbra Eclipse Medio Último Contacto con la Umbra Duración de la Totalidad Tiempo Total del Eclipse % Oscurecimiento - Magnitud - Dígitos Luna en Carta 19 de Marzo de 721 a. C. (-721) Total 19:19:53 hs. 21:13:05 hs. 23:06:18 hs. 01:37:12 hs. 03:46:24 hs. 100 % - 1,5219 - 12 dígitos Virgo 
Almagesto Observación - 19.03.721 a. C. Hora Salida de la Luna: 17:56:21 hs. Azimut: 265° 16'.
Nota del traductor al español: el cálculo de los dígitos es la fracción sombreada o eclipsada del diámetro lunar siendo igual a la Magnitud actual -menor o igual a 1- multiplicada por 12 dígitos (100% eclipsada). La carta y datos elaborados con mi software de aplicación "M1 Sistema Astronómico"©.
- ↑ Se supone que un eclipse total de Luna dura 4 horas desde el comienzo hasta el fin. Ello esta bien de acuerdo con la duración que uno deriva de las tablas de eclipses propias de Ptolomeo (Libro VI Capítulo 8) y con la presente duración máxima posible. La duración del eclipse en cuestión (Oppolzer no. 741) fue de hecho cerca de 3 ¾ hs.
- ↑ Esta diferencia de tiempo corresponde a la diferencia longitudinal de 12 ½º. La diferencia actual de tiempo es próxima a los 58 ½ minutos. En la Geografía Ptolomeo enmienda la diferencia, en la dirección correcta pero demasiado, por 1 ¼ horas (8.20.27), correspondiente a la diferencia entre las longitudes allí asignadas para Alejandría (de 60 ½º, 4.5.9) y para Babilonia (de 79º, 5.20.6).
- ↑ Cálculos modernos dan considerablemente un pequeño eclipse: Oppolzer (no. 743) 1,6 dígitos, Paul Viktor Neugebauer 1,5 dígitos. Sin embargo las propias tablas de Ptolomeo dan alrededor de 2 ½ dígitos: ver Cálculos, Ejemplo 11.
Fecha y horas calculadas con un programa de computación desde la observación realizada por los Babilonios (actual Bagdad) del siguiente:
Eclipse lunar Fecha Tipo Eclipse 1° Contacto con la Umbra Eclipse Medio Último Contacto con la Umbra Duración de la Totalidad Tiempo Total del Eclipse % Oscurecimiento - Magnitud - Dígitos Luna en Carta 8-9 de Marzo de 720 a. C. (-720) Parcial 22:44:25 hs. 23:25:08 hs. 00:05:51 hs. ------ 01:21:25 hs. 5,25 % - 0,1111 - 1,33 dígitos Virgo 
Almagesto Observación - 08.03.720 a. C. Nota del traductor al español: carta y datos elaborados con mi software de aplicación "M1 Sistema Astronómico"©.
- ↑ En un eclipse lunar la Luna esta diametralmente opuesta al Sol. Por lo tanto la salida de la misma coincide con la puesta del Sol, que ocurrió 5 ½ horas equinocciales antes de la medianoche. Ptolomeo asigna ½ hora para contar “luego de la salida de la Luna”. Él estima una duración de 3 horas para un eclipse de más de 6 dígitos, (de acuerdo a Oppolzer, no. 744, este eclipse tuvo una magnitud de 6,4 dígitos y una duración de 2;36h; Paul Viktor Neugebauer calcula 6,1 dígitos y 2,4 horas). Obviamente este eclipse apenas se "registra de forma inequívoca" (principio de este capítulo).
Fecha y horas calculadas con un programa de computación desde la observación realizada por los Babilonios (actual Bagdad) del siguiente:
Eclipse lunar Fecha Tipo Eclipse 1° Contacto con la Umbra Eclipse Medio Último Contacto con la Umbra Duración de la Totalidad Tiempo Total del Eclipse % Oscurecimiento - Magnitud - Dígitos Luna en Carta 1 de Septiembre de 720 a. C. (-720) Parcial 18:25:08 hs. 19:36:30 hs. 20:47:51 hs. ------ 02:22:43 hs. 45,06 % - 0,4914 - 5,89 dígitos Pisces 
Almagesto Observación - 01.09.720 a. C. Hora Salida de la Luna: 18:34:11 hs. Azimut: 284° 42'.
Nota del traductor al español: carta y datos elaborados con mi software de aplicación "M1 Sistema Astronómico"©.
- ↑ Este es un punto metodológico. Las Tablas de los Movimientos Medios de Ptolomeo están basadas, no sobre períodos exactos que toma de Hiparco, sino (para la anomalía) sobre una corrección aplicada al número derivado de esos períodos Libro IV Capítulo 7. Sin embargo, la corrección por sí misma esta basada en parte sobre los parámetros aquí derivados. En consecuencia es importante notar que la corrección no hace una diferencia sobre los pequeños intervalos aquí considerados (entre el primero y segundo eclipse esta [corrección] solamente es cerca de 1 segundo de arco). En el Libro IV Capítulo 11 es claro que Hiparco ya ha establecido el principio de que fue necesario utilizar un [conjunto] de tres eclipses cercanos en tiempos, por ende cualquier error en los movimientos medios a largo plazo podría tener un efecto mínimo.
- ↑ Ver HAMA 74 para un argumento detallado acerca de la ubicación del observador con respecto a los puntos sobre el epiciclo representando los tres eclipses.
- ↑ 115;41,24p (como en el manuscrito L) puede ser correcto en H309,10 (calculado como: 115;41,28p). No hay diferencias en los cálculos subsecuentes si uno adopta 21, 24 o 28.
- ↑ Euclides III 36: el rectángulo contenido por cualquier línea dibujada desde un punto fuera del círculo y el segmento de esa línea fuera del círculo es igual al cuadrado de la tangente al círculo desde ese punto.
- ↑ Euclides II 6: si una línea recta (LM) es bisecada y una línea recta (DM) agregada a ella, el rectángulo contenido en su totalidad más la línea agregada (LD) y la línea adicionada (DM), junto con el cuadrado sobre la mitad (KM²) es igual al cuadrado de la línea (DK) compuesta por la mitad (KM) y la línea agregada (DM).
- ↑ Oppolzer no. 2071, circunstancias que están de acuerdo con el informe de Ptolomeo.
Fecha y horas calculadas con un programa de computación desde la observación realizada por Ptolomeo (en Alejandría) del siguiente:Eclipse lunar Fecha Tipo Eclipse 1° Contacto con la Umbra Eclipse Medio Último Contacto con la Umbra Duración de la Totalidad Tiempo Total del Eclipse % Oscurecimiento - Magnitud - Dígitos Luna en Carta 6-7 de Mayo de 133 d. C. (133) Total 20:49:24 hs. 22:35:10 hs. 00:20:57 hs. 00:42:44 hs. 03:31:32 hs. 100 % - 1,067 - 12 dígitos Ophiuchus 
Almagesto Observación 06.05.133 d. C. Nota del traductor al español: carta y datos elaborados con mi software de aplicación "M1 Sistema Astronómico"©.
- ↑ Oppolzer no. 2074, circunstancias extremadamente de acuerdo con el informe de Ptolomeo.
Fecha y horas calculadas con un programa de computación desde la observación realizada por Ptolomeo (en Alejandría) del siguiente:Eclipse lunar Fecha Tipo Eclipse 1° Contacto con la Umbra Eclipse Medio Último Contacto con la Umbra Duración de la Totalidad Tiempo Total del Eclipse % Oscurecimiento - Magnitud - Dígitos Luna en Carta 20-21 de Octubre de 134 d. C. (134) Parcial 20:55:46 hs. 22:31:45 hs. 00:07:43 hs. ------ 03:11:57 hs. 86,51 % - 0,829 - 9,94 dígitos Taurus 
Almagesto Observación 20.10.134 d. C. Nota del traductor al español: carta y datos elaborados con mi software de aplicación "M1 Sistema Astronómico"©.
- ↑ Oppolzer no. 2075, circunstancias: eclipse medio 1;43 a.m. ≈ 3 ¾ horas después de la medianoche en Alejandría, magnitud: 5,5 dígitos.
Fecha y horas calculadas con un programa de computación desde la observación realizada por Ptolomeo (en Alejandría) del siguiente:Eclipse lunar Fecha Tipo Eclipse 1° Contacto con la Umbra Eclipse Medio Último Contacto con la Umbra Duración de la Totalidad Tiempo Total del Eclipse % Oscurecimiento - Magnitud - Dígitos Luna en Carta 6 de Marzo de 136 d. C. (136) Parcial 02:12:12 hs. 03:20:56 hs. 04:29:40 hs. ------ 02:17:28 hs. 38,47 % - 0,438 - 5,25 dígitos Virgo 
Almagesto Observación 06.03.136 d. C. Nota del traductor al español: carta y datos elaborados con mi software de aplicación "M1 Sistema Astronómico"©.
- ↑ Leer en cambio de en H317.4-5. Esto podría significar “No obstante, sin esto como una asunción”; sino que la ubicación del apogeo en el arco AB es (y debe ser) asumida en la Fig. 4.8. Supongo que (“similarmente”) fue corrompido a (“de cualquier modo”) y el resto luego adicionado como un antiguo glosario.
- ↑ Leer (en el manuscrito D, y el Ar) en cambio de en H317,25. Entonces también en H319,4 y en H319,14.
- ↑ Leer BEZ (en el manuscrito D, y el Ar) en cambio de BEZ en H318.8.
- ↑ Leer seg. en cambio de seg. (en todos los manuscritos) en H319,7. Lo último podría significar “donde DE, como fue demostrado, es igual a 120p”, que no tiene sentido, dado que esto es asumido, no probado. El manuscrito D, y el Ar tienen la misma [palabra] absurda en H318,11.
- ↑ Leer seg. , seg. (en el manuscrito D, y el Ar) en cambio de seg. , seg. en H321,14-15. Heiberg elimina desde lo último, aunque aún es muy absurdo.
