Almagesto: Libro VI - Capítulo 07
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
{Construcción de las Tablas de los Eclipses}
Por medio de lo [expresado] anteriormente nos tiene que empezar a ser claro qué intervalos entre las Sizigias deberían tomarse en cuenta cuando son examinados los eclipses. Ahora, después de haber determinado los tiempos del eclipse medio en esas [sizigias], y calculadas las posiciones de la Luna en aquellos instantes, (las posiciones aparentes en las conjunciones y las posiciones verdaderas en las oposiciones), queremos tener un medio conveniente para determinar, desde la posición de la Luna en latitud, en cuales de esas sizigias se producirá definitivamente un eclipse, y las magnitudes y los tiempos de oscurecimiento para esos eclipses. Para resolver este problema hemos construido unas tablas, dos para los eclipses solares y dos para los eclipses lunares ([en cada caso] una para la máxima distancia de la Luna y una para su mínima distancia). El intervalo que establecimos [entre las sucesivas entradas en las tablas] esta determinada por la cantidad de Oscurecimiento, siendo 1/12 ma. parte del diámetro de cualquiera de las luminarias eclipsadas [2].
La primera tabla de los eclipses solares, que cubren el intervalo entre los límites de los eclipses en la mayor distancia de la Luna, estará arreglada en 25 líneas y en 4 columnas. Las dos primeras columnas contendrán la posición aparente de la Luna en [el argumento de] la latitud sobre el círculo inclinado [de la Luna] para cada [unidad de] oscurecimiento. Dado que el diámetro del Sol es de 0;31,20º, y, como fue probado en el Libro V al final del capítulo 14, el diámetro de la Luna en su mayor distancia es también de 0;31,20º, [entonces] seguido esto, cuando el centro aparente de la Luna esta a 0;31,20º desde el centro del Sol sobre el gran círculo a través de ambos centros, (y por lo tanto esta a 6º desde el Nodo a lo largo de su círculo inclinado, de acuerdo a la proporción previa, de 11;30 / 1), esta será la ubicación en la que la Luna justamente toca el Sol. Entonces en la primera línea de la primera columna ponemos [(escribimos)] "84º", y en la primera línea de la segunda columna, "276º"; nuevamente, en la última línea de la primera columna ponemos "96º", y en la última línea de la segunda columna, "264º".
Además, dado que la cantidad del círculo inclinado [de la Luna] que corresponde a la 1/12 ma. parte del diámetro solar es de alrededor de 0;30º [3], incrementamos o disminuimos por esta cantidad las entradas en las dos columnas arriba mencionadas, comenzando por las líneas en ambos finales y yendo hacia la mitad. Sobre la línea media ponemos "90º" y "270º".
La tercera columna contendrá la magnitud del oscurecimiento. Sobre las dos líneas de arriba y de abajo ponemos un "0" representando la posición de contacto, en las dos líneas siguientes a esas "1 dígito" (representando 1/12 ma. parte del diámetro), y así sucesivamente para el resto, con un incremento [de línea en línea] de 1 dígito hasta la línea media, que recibirá la entrada de "12 dígitos".
La cuarta columna contendrá la distancia atravesada por el centro de la Luna correspondiente a cada oscurecimiento [tabulado], aunque teniendo en cuenta tanto el movimiento adicional del Sol [durante la fase del eclipse] o la epiparalaje de la Luna [4] [por ej. el cambio en la Paralaje Lunar].
La segunda tabla para los eclipses solares, que cubre el intervalo entre los límites de los eclipses en la mínima distancia de la Luna, será arreglada por el mismo camino como la primera, excepto que tendrá 27 líneas y en 4 columnas. El radio de la Luna en su distancia mínima es, como hemos demostrado de 0;17,40º (Libro VI en la mitad del Capítulo 5), donde el radio del Sol es de 0;15,40º. Entonces cuando la Luna [en su mínima distancia] esta justamente tocando el Sol, su centro aparente esta a 0;33,20º desde el centro del Sol, y a 6;24º desde el nodo a lo largo de su círculo inclinado. Entonces [5] las entradas para [el argumento] aparente de la latitud en las líneas de arriba y de abajo son "83;36º, 276;24º", y "96;24º, 263;36º" [respectivamente], y la entrada de los dígitos sobre la línea media, si utilizamos Interpolación Lineal [6], será de 12 4/5 dígitos. Para esta entrada también habrá una duración de la totalidad [7].
Cada una de las Tablas de los Eclipses Lunares estarán arregladas en 45 líneas y en 5 columnas. En la primera tabla tabularemos el [argumento de la latitud] para la máxima distancia de la Luna. El radio de la Luna en su máxima distancia es, como hemos demostrado (Libro V al final del Capítulo 14), de 0;15,40º, y el Radio de la Sombra, de 0;40,44º. Entonces, cuando la Luna esta justo tocando la sombra, el centro de la Luna esta a 0;56,24º desde el centro de la sombra a lo largo del gran círculo a través de ambos centros, y a 10;48º desde el nodo a lo largo del círculo inclinado [de la Luna]. Ponemos, sobre la primera línea, "79;12º" [en la primera columna] y "280;48º" [en la segunda columna], y en la última línea "100;48º" y "259;12º". Por el mismo razonamiento como en la primera [Tabla Solar], incrementamos o restamos cada línea por 0;30º, que corresponde a la 1/12 ma. parte del diámetro lunar para esa distancia.
En la segunda tabla tabularemos el [argumento de] la latitud para la Luna en la menor distancia, en la que, como hemos demostrado (Libro VI en la mitad del Capítulo 5), su radio es de 0;17,40º, y el radio de la sombra de 0;45,56º. Por lo tanto, cuando la Luna justo toca la sombra, su centro esta, por el mismo argumento como el de antes, a 1;3;36º desde el centro de la sombra, y a 12;12º desde el nodo a lo largo del círculo inclinado de la Luna. Por lo tanto ponemos, en la primer línea, "77;48º" y "282;12º", y, en la última línea, "102;12º" y "257;48º", y nuevamente incrementamos o disminuimos las entradas por una cantidad correspondiente a la 1/12 ma. parte del diámetro lunar para esa distancia, [a saber] de 0;34º.
La tercera columna [en cada tabla], para los dígitos, estará arreglada por el mismo camino como las Tablas Solares. Entonces también lo serán las columnas sucesivas, que contienen el recorrido de la Luna para cada oscurecimiento [tabulado], a saber [la cuarta columna] para ambas inmersiones y emersiones [egresos], y también [la quinta columna] para la mitad en la totalidad.
Calculamos el recorrido de la Luna tabulada geométricamente para cada oscurecimiento, pero como si [el problema fuera confinado a] un único plano y de líneas rectas, puesto que tales pequeños arcos no difieren sensiblemente de las cuerdas correspondientes, y además el movimiento de la Luna en su círculo inclinado no es notablemente diferente desde su movimiento con respecto a la Eclíptica.
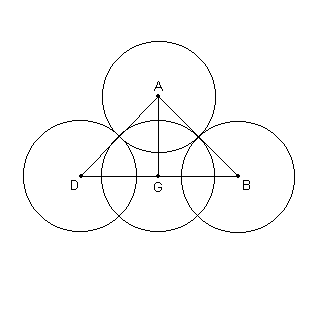
[Digo esto] por si alguien supusiera que no nos damos cuenta de que, en general, el movimiento en longitud de la Luna es afectado por el uso de los arcos del círculo inclinado en cambio de los arcos de la eclíptica, y también no prosigue que el tiempo de la sizigia es exactamente el mismo como el tiempo del eclipse medio. [Para ilustrar esto, ver la Fig. 6.2], cortamos desde el nodo A dos arcos iguales, AB y AG, de los círculos en cuestión [de la órbita y de la elíptica], uniendo BG y desde B dibujar BD perpendicular a AG. Entonces es inmediatamente obvio que, si suponemos la Luna [ubicada] en B, cuando utilizamos el arco AG de la eclíptica en cambio del arco AD, entonces, dado que el movimiento con respecto a la eclíptica esta determinado por [el gran círculo] a través de los polos de la eclíptica, la diferencia [en longitud] debida a la inclinación de la órbita lunar será GD.

O nuevamente, si imaginamos el Sol o el centro de la sombra en B [8], el tiempo de la sizigia ocurrirá cuando la Luna esta en G ([podemos decir esto] ya que la diferencia es insignificante debido a los dos círculos de [la eclíptica y de la órbita]), aunque el tiempo del eclipse medio cuando la Luna esta en D, dado que, de nuevo, el tiempo del eclipse medio esta definido por el círculo a través de los polos de la órbita de la Luna. Y [por lo tanto] el tiempo de la sizigia diferirá del tiempo del eclipse medio por el arco GD.

La razón de que no tomamos en cuenta estos arcos en nuestras derivaciones de las [entradas] individuales es que las diferencias que ellos causan son pequeñas e imperceptibles. Mientras podría ser absurdo no reconocer cualquiera de estos efectos, por otro lado, cuando uno considera la complicación resultante de los métodos necesarios para hacer frente a cada uno de ellos, el abandono deliberado de los efectos suficientemente pequeños como para ser pasados por alto tanto en la teoría y en las observaciones evoca [en el lector] una fuerte sensación de ventaja de mayor simplicidad, y sin arrepentirse, ni mínimamente, por el error resultante en la representación de los fenómenos. En algún caso, encontramos que el arco correspondiente a GD no excede, en general, los 0;5º. Esto puede ser demostrado por medio del mismo teorema que utilizamos (Libro I Capítulo 16) para calcular la diferencia entre los arcos del Ecuador y los arcos correspondientes de la eclíptica, como definido por un [gran] círculo dibujado a través de los polos del Ecuador. Y en los eclipses [el arco correspondiente a GD] no excede los 2'.
Porque si tomamos el arco AB = arco AG = 12º, que es la máxima cantidad de la distancia a la Luna [desde el nodo] en los eclipses, entonces BD es de alrededor de 1º. Y por lo tanto AD esta cerca de 11;58º, y, por sustracción, GD es de 2', que corresponde a menos de la 1/16 ta. parte de una hora equinoccial [9]. La precisión escrupulosa sobre una cantidad tan pequeña es un signo de vanidad en lugar del amor por la verdad.
Por las razones arriba [expresadas] hemos calculado la trayectoria de la Luna durante los oscurecimientos en cuestión como si los círculos [de la eclíptica y de la órbita] fueran sensiblemente idénticos. El método de cálculo, dando uno o dos ejemplos, es el siguiente.
Sea A [Fig. 6.3] [10] el centro del Sol o de la sombra, y BGD la línea recta representando el arco del círculo [inclinado] de la Luna. Sean los puntos [B y D] representando el centro de la Luna cuando esta tocando justo el Sol o la Sombra, en B la aproximación de la Luna [por ej. en el primer contacto], y en D su retiro [por ej. en el último contacto]. Unir AB y AD, y eliminar la perpendicular AG desde A hacia BD.

Ahora es claro que el eclipse medio y su mayor oscurecimiento ocurren cuando el centro de la Luna esta en G, porque [1] AB es igual a AD, y por lo tanto las distancias recorridas, BG y GD, son también iguales, y porque [2] AG es la menor de todas las líneas uniendo los dos centros [cuando la Luna está] en BD. También es claro que AB y AD, cada uno, comprende la suma de los radios de la Luna y del Sol o la [suma de la Luna] y de la sombra, y que cada uno de ellos excede AG por aquella parte del diámetro del cuerpo eclipsado que esta cortado por el oscurecimiento.
Siendo este el caso, sea el oscurecimiento, por ej., de 3 dígitos. Primero sea A representando el centro del Sol.
Por lo tanto [11], cuando la Luna esta en su mayor distancia,
AB = 31;20 minutos (principio de este capítulo)
en consecuencia AB² = 981;47.
Y AG = 23;30 minutos, dado que es menor que AB por una 3/12 ma. parte del diámetro del Sol, por ej. 7;50 minutos.
Entonces AG² = 552;15.
Por lo tanto BG² = 429;32,
y BG ≈ 20;43 minutos.
Esta es la cantidad que entraremos en la cuarta columna de la primera Tabla de los Eclipses [Solares] para los "3 dígitos" opuestos.
Para la mínima distancia de la Luna
AB = 33;20 minutos (principio de este capítulo)
en consecuencia AB² = 1111;7.
Y AG = [0;33,20º - 0;7,50º =] 25;30 minutos,
entonces AG² = 650;15.
Y, por sustracción, BG² = 460;52,
y entonces BG = 21;28 minutos.
Esta es la cantidad que entraremos en la cuarta columna en la segunda Tabla de los Eclipses [Solares] para los "3 dígitos" opuestos.
Seguido, sea A que representa el centro de la sombra, y sea el oscurecimiento la misma fracción anterior, de ¼, [pero ahora] del diámetro lunar.
Entonces, para la máxima distancia de la Luna,
AB = 56;24 minutos (al comienzo de este capítulo),
entonces AB² = 3180;58.
y AG = 48;34 minutos, dado que este es menor que AB por ¼ del diámetro lunar, por ej. (para la máxima distancia de la luna) por 7;50 minutos.
Entonces AG² = 2358;43.
Por lo tanto, por sustracción, BG² = 822;15,
y BG = 28;41 minutos.
Esta es la cantidad que entraremos en la cuarta columna de la primera Tabla de los [Eclipses] Lunares para los "3 dígitos" opuestos. Esta representa el recorrido durante la inmersión, que es sensiblemente igual a aquella durante la emersión.
Para la mínima distancia [de la Luna]
AB = 63;36 minutos (comienzo de este capítulo),
entonces AB² = 4044;58.
Y AG = 54;46 minutos, dado que la diferencia [entre AB y AG es de] 8;50 minutos, es nuevamente, de ¼ del diámetro de la Luna, [aquí] en la mínima distancia.
En consecuencia AG² = 2999;23.
Entonces, por sustracción, BG² = 1045;35,
y BG = 32;20 minutos.
Esta es la cantidad que entraremos como los "3 dígitos" opuestos, como antes, en la cuarta columna de la segunda Tabla de los [Eclipses Lunares].

Seguido, para representar aquellas [fases del] oscurecimiento lunar comprendiendo la duración de la totalidad, sea A [Fig. 6.4] el centro de la sombra, y BGDEZ la línea recta permanente del arco del círculo inclinado de la Luna. Sea B que representa el lugar del centro de la Luna cuando [(el limbo lunar)] esta justo tangente externamente al círculo de la sombra, en [su] aproximación, G el lugar del centro de la Luna cuando [(el limbo lunar)] esta justo tangente interiormente al círculo de la sombra en el comienzo de la totalidad, E el lugar del centro de la Luna cuando [(el limbo lunar)] esta justo tangente al círculo de la sombra cuando [la Luna] se [va] retirando [al final de la totalidad], y Z el lugar del centro de la Luna cuando [(el limbo lunar)] esta tangente externamente a la sombra ya bastante al final de su egreso [del oscurecimiento].
Nuevamente eliminar la perpendicular AD desde A hasta BZ. Las mismas conclusiones como las de antes se mantienen válidas, y además es claro que AG y AE cada uno comprende la cantidad por la que el radio de la sombra excede el radio de la Luna. Por lo tanto la distancia GD es igual a la distancia DE, y cada uno representa mitad de la totalidad, mientras BG, el resto [de BD - GD], que representa la inmersión, es igual a EZ, el resto [de DZ - DE], que representa el egreso [(emersión)].

Entonces [como ejemplo] tomemos un eclipse cuya entrada [en la tabla] es de "15 dígitos lunares", por ej. un [eclipse] en el que D, el centro de la Luna [en el eclipse medio], yace a 1 ¼ diámetros lunares dentro de la frontera establecida por los límites del eclipse. Es decir que, cuando
(AB - AD) = (AZ - AD) = 1 ¼ diámetros lunares
y (AG - AD) = (AE - AD) = ¼ diámetros lunares.
Luego, de la máxima distancia de la Luna,
como antes (expresado más arriba), AB = 56;24 minutos y AB² = 3180;58.
Y AG = 25;4 minutos, dado que el diámetro de la Luna en la máxima distancia es de 31;20 minutos.
En consecuencia AG² = 628;20,
y, por un argumento similar,
AD = [56;24 - (31;20 + 7;50) =] 17;14 minutos y
AD² = 296;59.
Entonces, por sustracción [de AD² desde AB²], BD² = 2883;59,
BD = 53;42 minutos.
Y, por sustracción [de AD² desde AG²], GD² = 331;21,
y GD = 18;12 minutos.
Entonces, por sustracción, BG = 35;30 minutos.
Entonces pondremos, opuesta a la entrada de "15 dígitos" en la primera Tabla de los Eclipses Lunares, en la cuarta columna, "35;30 minutos" para la inmersión (que será la misma para la emersión), y, en la quinta columna "18;12 minutos" para la mitad de la duración de la totalidad.
La mínima distancia de la Luna,
como antes (expresado más arriba), AB = 63;36 minutos
y AB² = 4044;58;
AG = 28;16 minutos, dado que, como demostramos, el diámetro de la Luna en su mínima distancia es de 35;20 minutos,
y AG² = 799;0.
Y, por un argumento similar, AD = [63;36 - (35;20 + 8;50) =] 19;26 minutos,
entonces AD² = 377;39.
Por lo tanto, por sustracción, BD² = 3667;19,
y BD = 60;34 minutos.
Y, por sustracción, GD² = 421;21
y GD = 20;32 minutos.
Entonces, por sustracción, BG = 40;2 minutos.
Por lo tanto pondremos, opuesta a la entrada "15 dígitos" en la segunda Tabla para los Eclipses Lunares, en la cuarta columna "40;2 minutos" para la inmersión (que será nuevamente la misma para la emersión), y, en la quinta columna, "20;32 minutos" para la mitad de la duración de la totalidad.
Con el fin de tener un modo conveniente para obtener la fracción de la diferencia [entre los valores derivados desde la primera y segunda tabla] para las posiciones de la Luna sobre el Epiciclo entre las máximas y mínimas distancias ([que determinamos] por el método [de interpolación] de las sexagésimas partes), hemos dibujado, debajo de las tablas superiores, otra tabla más pequeña. Esta contiene, como argumento, la posición [en anomalía] sobre el epiciclo, y, [como función], el correspondiente número de las sexagésimas a ser aplicado [como coeficiente de interpolación] en cada caso a la diferencia [entre los valores] derivados desde [12] la primera y la segunda Tabla de los Eclipses. Ya hemos calculado las cantidades de esas sexagésimas [partes] para la Tabla de la Paralaje Lunar: están colocadas en la séptima columna [de la tabla], dado que el epiciclo ha de ser tomado en el apogeo de la Excéntrica para representar [su ubicación en] la sizigia.
Pero la mayoría de aquellos que observan las indicaciones [del tiempo (clima)], el tamaño del oscurecimiento derivado de las mediciones en los eclipses, no por los diámetros de los discos [del Sol y de la Luna], sino, en su totalidad, por [la cantidad de] la superficie total de los discos [13], dado que, cuando uno se aproxima ingenuamente al problema, el ojo compara toda la parte de la superficie que es visible con la total de aquella que es invisible. Por esta razón hemos aún agregado a la tabla de arriba otra pequeña tabla con 12 líneas y 3 columnas. En la primera columna ponemos los Dígitos de 1 a 12, donde cada dígito representa 1/12 ma. parte de diámetro de cada luminaria, como en las presentes Tablas de los Eclipses. En las otras dos columnas ponemos duodécimas partes de toda el área superficial correspondiendo a esos [dígitos lineales], aquellas para el Sol en la segunda, y aquellas para la Luna en la tercera. Calculamos estas cantidades solo para los tamaños [de los diámetros aparentes] para la Luna en su distancia media, dado que muy cerca la misma proporción resultará [en otras distancias], dando una pequeña variación en los diámetros. Además, asumimos que la proporción de la circunferencia con el diámetro es de 3;8,30 / 1, dado que esta razón esta cerca a medio camino entre (3 1/7) / 1 y (3 10/71) / 1, las cuáles Arquímedes utilizó como [límites] vagos [(no muy precisos)] [14].
Primero, para representar los eclipses solares [Fig. 6.5], sea ABGD el disco del Sol con centro en E, y AZGH el disco de la Luna en la distancia media con centro en Θ, intersecando el disco del Sol en los puntos A y G. Unir BEΘH, y supongamos que ¼ del diámetro del Sol esta eclipsado.
Por lo tanto ZD = 3 donde el diámetro BD = 12,
y el diámetro de la Luna, ZH ≈ 12;20 en las mismas unidades, de acuerdo a la proporción 15;40 / 16;40 [15].
Por lo tanto EΘ = [½ * (12 + 12;20) - 3 =] 9;10 en las mismas unidades.
Por lo tanto las circunferencias de los discos son, de acuerdo a la proporción 1 / 3;8,30,

la circunferencia del Sol: 37;42p
la circunferencia de la Luna: 38;46p.
De igual manera, dado que el producto del radio y de la circunferencia es dos veces el área del círculo, las áreas totales de los discos son:
el área del Sol: 113;6p
el área de la Luna: 119;32p.
Con lo anterior como cantidades dadas, sea el problema encontrar el área de la superficie encerrada por ADGZ, donde el área total de la superficie del Sol es de 12 partes.
Unir AE, AΘ, GE, GΘ, y también dibujar la perpendicular AKG.
Ahora, donde EΘ = 9;10p,
AE = EG = 6p (por asunción).
y AΘ = ΘG = 6;10p (por asunción).
Además, el ángulo en K es recto.
Por lo tanto, si dividimos (ΘA² - AE²), o 2;2, por EΘ, tendremos (KΘ - EK) como 0;13 ⅓p [16].
Por lo tanto EK resulta 4;28p y KΘ de 4;42p.
En consecuencia AK = KG ≈ 4p.
De acuerdo con el área del triángulo AEG = 17;52p
y el área del triángulo AΘG = 18;48p.
Además, donde el diámetro BD = 12p y ZH = 12;20p, AG = 8p;
entonces donde el diámetro BD = 120p, AG = 80p,
entonces donde el diámetro ZH = 120p, AG = 77;50p.
Por lo tanto los arcos correspondientes son:
arco ADG = 83;37º del círculo ABGD
y arco AZG = 80;52º del círculo AZGH.
Entonces, ya que la proporción de un círculo con uno de sus arcos es igual a la proporción del área del círculo total con el área del sector por debajo de ese arco,
área del sector AEGD = 26;16p donde el área del círculo ABGD = 113;6p, como fue demostrado,
y, en las mismas unidades, el área del sector AΘGZ = 26;51p
(dado que el círculo AZGH fue demostrada ser de 119;32p).
Y, en las mismas unidades, demostramos que
área del triángulo AEG = 17;52p
y área del triángulo AΘG = 18;48p.
Por lo tanto, por sustracción, el área del segmento ADGK = 8;24p y el área del segmento AZGK = 8;3p. Entonces, por adición, el área de AZGD = 16;27p donde el área del círculo ABGD = 113;6p. Por lo tanto donde el área del disco del Sol es igual a 12p, el área de la parte eclipsada ≈ 1 ¾p. Esta es la cantidad que entraremos en la tabla arriba mencionada en la segunda columna en la línea con "3 dígitos" [como argumento].
Nuevamente, en la misma figura [Fig. 6.5], representando los eclipses lunares, sea ABGD el disco de la Luna, y AZGH el disco de la sombra en la distancia [lunar] media, y, como antes, sea eclipsado ¼ ta. [parte] del diámetro de la Luna.
Por lo tanto, donde el diámetro BD = 12p, la sección eclipsada, ZD = 3p. Y, de acuerdo a la proporción 2;36 / 1, el diámetro de la sombra, ZH = 31;12p. Por lo tanto EKΘ viene a ser [½ * (12 + 31;12) - 3 =] 18;36p.
Entonces las circunstancias son las siguientes:
| el disco de la Luna: | 37;42p |
| el disco de la sombra: | 98;1p |
y las áreas son:
| el disco de la Luna: | 113;6p |
| el disco de la sombra: | 764;32p |
Aquí nuevamente, donde EΘ = 18;36p,
AE = EG = 6p (por asunción)
y AΘ = ΘG = 15;36p (por asunción).
En consecuencia (KΘ - EK) = (ΘA² - AE²) / EΘ = 11;8p.
Entonces EK llega a 3;44p y KΘ a 14;52p.
Por lo tanto AK = KG = 4;42p.
De acuerdo, al área del triángulo AEG = 17;33p
y el área del triángulo AΘG = 69;52p.
Por lo tanto, donde el diámetro BD = 12p y ZH = 31;12p, AG = 9;24p.
Entonces donde el diámetro BD = 120p, AG = 94p,
y donde el diámetro ZH = 120p, AG = 36;9p.
Por lo tanto los arcos correspondientes son:
arco ADG = 103;8º del círculo ABGD
y arco AZG = 35;4º del círculo AZGH.
Por lo tanto, por el argumento anterior, el área del sector AEGD = 32;24p donde, como fue demostrado, el área del círculo ABGD = 113;6p y, en las mismas unidades, el área del sector AGΘZ = 74;28p, dado que el área del círculo AZGH fue mostrada ser de 764;32p.
Y, como demostramos, en las mismas unidades
| el área del triángulo AEG = | 17;33p |
| y el área del triángulo AΘG = | 69;52p |
Por lo tanto, por sustracción, el área del segmento ADGK = 14;51p
y el área del segmento AZGK = 4;36p.
Entonces, por adición, el área comprendida por AZGD es de 19;27p,
donde el área del círculo ABGD es tomada como de 113;6p.
Por lo tanto, donde el área del disco lunar es de 12p,
el área comprendida por su sección eclipsada será por alrededor de 2 1/15p.
Esta es la cantidad que entraremos en la tabla, lunar arriba mencionada, en la tercera columna, sobre la línea "3 dígitos" [como argumento].
Los diseños de las tablas son los siguientes.
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Libro VI |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 | 11 | 12 |
| 13 |
Notas de referencia
- ↑ Ver HAMA 134-41, Pedersen 231-5.
- ↑ Por ej. los intervalos entre los argumentos sucesivos en las tablas (cols. 1 y 2 en la Tabla del Libro VI Capítulo 8) son determinados tomando valores enteros de la magnitud (col. 3), en contraste con el procedimiento normal, en el que uno toma el argumento a intervalos puramente arbitrarios. Esto es más conveniente para el compilador de las tablas que para el usuario, aunque ello persiste en las tablas de los eclipses de las Tablas Manuales (Prácticas) y en muchas de las tablas medievales derivadas desde ellas (ver el ej. en Toomer [10] no. 59. 88).
- ↑ (0;31,20 / 12) * 11 ½ = 0;30,2 ≈ 0;30.
- ↑ Diferencia entre la primera y la segunda paralaje lunar.
Nota del traductor al español. - ↑ El texto de Heiberg en este parágrafo esta desordenado. Para producir una secuencia lógica, insertar un punto y aparte al final de la línea 501,9, comenzar la próxima sentencia () dia (en el manuscrito Ar), remover el punto y aparte al final de 501,17, y eliminar la [palabra] (en los manuscritos D y Ar) en 501,18.
- ↑

Método de Interpolación por Lagrange. Click en la imagen para ampliar
Fórmula de interpolación solamente entre 2 pares de valores o puntos (X;Y), (i = 0 y 1 en Fórmula Polinómica de Lagrange).
α es el argumento a "entrar" en la columna de las X y el "Valor Interpolado" resulta de la columna de las Y.
Para una interpolación con más de 2 pares de valores (X;Y) verː Método de Interpolación por Lagrange, aunque para los valores que interpola Ptolomeo, con esta fórmula sencilla y reemplazándola con los 4 valores de una tabla, da el mismo resultado que el del astrónomo.
Nota del traductor al español. - ↑ El intervalo del argumento correspondiente a 1 dígito de la magnitud de un eclipse es de 0;30º en otra parte de la tabla. Dado que el intervalo es aquí de 0;24º, la cantidad correspondiente en dígitos es de 4/5. Cálculos precisos del radio de 0;17,40º y 0;15,40º dan la magnitud máxima en un eclipse solar como de 12;46 dígitos. La cantidad mas allá de los 12 dígitos representa la "duración de la totalidad" (), como en los eclipses lunares. Ver también Libro VI Capítulo 8 nota de referencia nro. 8.
- ↑ Por ej. los dos arcos ahora están intercambiados, siendo AB la eclíptica y AG la órbita de la Luna. En cambio de usar la misma figura, Ptolomeo debería haber dibujado otra, en la cual GB es perpendicular a AB (por ej. AB ≠ AG). Comparar la Fig. J (tomada de Manitius 452-53), que muestra que la sizigia verdadera (en G) precede al eclipse medio (en D) antes del nodo, sino que lo sucede después del nodo.
- ↑ Cf. HAMA 83 n. 5, estimando un error máximo de 6' como resultado de omitir la inclinación de la órbita lunar en el cálculo de las longitudes. Utilizando la formula tan λ = tan ω * cos ι, encuentro, para ι = 5º, la máxima diferencia entre λ y ω siendo alrededor de 6 ½' para ω ≈ 45;3º. Utilizando la misma fórmula para ω = 12º, encuentro que λ = 11;57,20º, por lo tanto GD = 0;2,40º, que aún genera menos que la 1/12 ma. parte de una diferencia de hora en el instante del eclipse medio. Ptolomeo calcula erróneamente BD ≈ AB / (11 ½) ≈ 1, AD = (12² - 1²) ^ 0,5 ≈ 11;58.
- ↑ Las Figs. 6.3 y 6.4 se dilucidan por las Figs. K y L respectivamente, en las que los círculos representando al Sol, a la Luna y a la sombra están dibujados en ellas. Estas son tomadas de Manitius, pero también son muy similares a los diagramas alternativos encontrados en el manuscrito D.
- ↑ Leer (con el manuscrito D) en cambio de en H507,3.
- ↑ Leer en cambio de ("que aparece desde") en H512,1. También encontrado en todos los manuscritos Griegos y en parte de la tradición Árabe, la última [palabra] no tiene paralelo en el Almagesto, y debe ser reemplazada por una palabra como (cercana paleográficamente), o , H385,5-7, . El manuscrito Is tiene la [frase] "allati tukraju", la cual sostiene mi enmienda.
- ↑ Aunque no hay razón para dudar sobre la declaración de Ptolomeo, yo se que no [hay] una magnitud en un antiguo eclipse sobreviviente en el que inequívocamente sea dada en esa "área de dígitos".
- ↑ Arquímedes, "Mediciones del Círculo", ed. Heiberg I 232-42, tr. Heath 91-8.
- ↑ El radio del Sol es de 0;15,40º (Libro VI Capítulo 5 Fig. 6.1). El radio de la Luna en su distancia media es el promedio entre 0;15,40º y 0;17,40º, por ej. 0;16,40º. Aunque Ptolomeo ha cometido un error de cálculo (cf. Manitius p. 385 n. b) y Papo de Alejandría, (Rome [1] I 261): 12 * (16;40 / 15;40) ≈ 12;46, no 12;20. Esto afecta la precisión en cada entrada en la segunda columna, aunque los resultados entonces están toscamente redondeados siendo esto de poca importancia.
- ↑ Dado que ΘA² - AK² = KΘ², AE² - AK² = EK²; sustrayendo, ΘA² - AE² = KΘ² - EK² = (KΘ + EK) * (KΘ - EK) = EΘ * (KΘ - EK). En H514,20 leo seg. ' (en el manuscrito A, D² e Is) en cambio de seg. seg. (13;3'). Corregido por Rome [1] I 262 n. (3), y por consiguiente Neugebauer en la 2da. edición de Manitius.

