Almagesto: Cálculos
| Ir a: Astrónomos en el Almagesto | Contenidos | Ir a: Catálogo de Estrellas de Ptolomeo. Datación en el Almagesto |
Ejemplos de Cálculos según el Almagesto
Ejemplo 1 - a) Calcular la distancia desde el Sol hasta el solsticio de verano y b) Hallar la latitud terrestre
(a). Libro II Capítulo 4. Dada la latitud terrestre (φ), calcular (Δλ) la distancia desde el Sol hasta el solsticio de verano medido a lo largo de la eclíptica.
Ejemplo: φ = 4;15º (cf. Libro II Capítulo 6, característica nro. 2, segundo paralelo).
- Desde la Tabla de las Inclinaciones:
| λ Arco de la Eclíptica | δ Arco del Meridiano |
|---|---|
| 10° | 4;1,38º |
| 11° | 4;25,32º |
- Por consiguiente, para una declinación [declinación solar = latitud terrestre φ] de 4;15º le corresponde una longitud eclíptica (contada desde el equinoccio de primavera) de 10;33,33º.
- Por lo tanto, la distancia desde el solsticio de verano, Δλ = (90º - 10;33,33º) = 79;26,27º (en el texto: 79 ½º).
- Por consiguiente, para una declinación [declinación solar = latitud terrestre φ] de 4;15º le corresponde una longitud eclíptica (contada desde el equinoccio de primavera) de 10;33,33º.
| Ver Fig. 1.15 en el Libro I Capítulo 14. HΘ = δ es el arco del meridiano que aquí es igual a 4;15°, es decir la declinación del Sol e igual a la latitud terrestre, por lo tanto el Sol en el cenit. Estos 4;15° se entrarán entre los dos valores de la segunda columna (δ) de la tabla y se interpolará [1] para hallar λ = EH el arco de la eclíptica, medido desde la intersección de la eclíptica con el ecuador (equinoccio de primavera) hasta su intersección con el meridiano ZHΘ. Δλ = HB es la distancia desde H hasta el solsticio B, aunque B es el solsticio de invierno, pero la figura es válida, simplemente cambiar la posición del ZHΘ de manera opuesta. Nota del traductor al español |
(b). Libro II Capítulo 6 Característica nro. 34. Hallar la latitud terrestre (φ) en la que el Sol no se pone para un período de tiempo dado.
Ejemplo: dado el período de un mes. Tomando un mes de 30 días, y asumiendo que el Sol se mueve 1 °/día sobre la eclíptica, hallamos que el paralelo en cuestión corta 30º de la eclíptica, o 15º a ambos lados del solsticio de verano.
- Desde la Tabla de las Inclinaciones:
| λ Arco de la Eclíptica | δ Arco del Meridiano |
|---|---|
| 90º - 15º = 75º | 22;59,41º |
- Por consiguiente φ = 90º - δ = 90° - 22;59,41º = 67;0,19º (en el texto: 67º).
[Se entra con 75° en la columna λ de la Tabla y se halla directamente el valor de δ, aquí 22;59,41º].
Ejemplo 2 - Hallar la longitud del día o de la noche
Libro II Capítulo 9. Dadas la longitud del Sol (λ☉) y la latitud terrestre (por ej. el "clima"), hallamos la longitud del día o de la noche y la longitud de la hora de estación.
Ejemplo: λ☉ = ♐︎ 28;18º. Lugar: Babilonia (cf. primer eclipse del Libro IV Capítulo 11). ¿Cuál es la longitud de la noche?
Utilizamos la Tabla de los Tiempos de Salida para Rodas (M = 14 ½ horas).
(a) Primer método.
Dado que es de noche, tomamos los grados opuestos al Sol, ♊︎ 28;18º.
Desde la Tabla:
| Interpolar [1] en "Intervalo de 10°" con | Grados de Tiempo Acumulado Interpolados |
|---|---|
| ρ (♊︎ 28;18º) | 69;27º |
| ρ (♐︎ 28;18º) | 286;50º |
| Diferencia (en el orden de los signos), Δ: | 217;23º |
Longitud de la noche en horas equinocciales es Δ/15: 14;29 horas (en el texto: 14 ⅖ horas).
Longitud de 1 hora nocturna de estación en grados de tiempo es Δ/12: 18;7º (en el texto: 18º)
(por consiguiente la longitud de 1 hora de estación en horas equinocciales es Δ/(12 * 15): 1;12,28 horas ).
(b) Segundo método.
De la Tabla de los Tiempos de Salida en la columna Esfera Recta:
| Interpolar [1] en "Intervalo de 10°" con | Grados de Tiempo Acumulado Interpolados |
|---|---|
| α (♊︎ 28;18º) | 88;9º |
| ρ (♐︎ 28;18º) | 69;27º |
| Diferencia (Δ): | 18;42º |
| Δ/6: | 3;7º |
Dado que Gemini esta al Norte de la eclíptica, sumar 15º, entonces (3;7° + 15°): 18;7º
Esta es la longitud de 1 hora nocturna de estación en grados de tiempo,
y en horas equinocciales (18;7° / 15): 1;12,28 hs.
Ejemplo 3 - Convertir el tiempo de horas de estación en tiempo de horas equinocciales
Desde la mitad hasta el final del Libro II Capítulo 9. Dada la longitud de una hora de estación en grados de tiempo, convertir el tiempo de horas de estación en tiempo de horas equinocciales.
Del Ejemplo 2 (q.v.), longitud de 1 hora nocturna de estación: 18;7º.
Luego de la medianoche ¿Cuántas horas equinocciales son 5 ½ horas de estación?
5 ½ * 18;7° / 15° = 6;38, entonces el tiempo es de 6;38 a.m. (06:38 horas).
Ptolomeo (l.c.) multiplica (18° / 15°) * 5 ½ y le da 6 ⅗ horas equinocciales (06:36 hs.) después de la medianoche.
Ejemplo 4 - Hallar el punto de la eclíptica en el que esta saliendo (el "horóscopo")
Desde la mitad hasta el final del Libro II Capítulo 9. Dada la longitud del Sol (λ☉), la latitud terrestre, y el tiempo en horas de estación, hallar el punto de la eclíptica en el que esta saliendo (el "horóscopo").
Ejemplo (cf. Libro VII Capítulo 3 - 4° observación). λ☉: ♏︎ 13;17º (en el texto, "alrededor de la mitad de ♏︎")
Lugar: Alejandría. Tiempo: 2 ¼ horas de estación después de la medianoche [2].
| cf. Ejemplo 2. Longitud de 1 nocturna (λ☉ = ♏︎ 13;17º, M = 14 hs.) | 16;38º |
| Tiempo desde la Puesta del Sol: 8 ¼ * 16;38°: | 137;14º |
| Desde la Tabla de los Tiempos de Salida para el Clima III (Soene): ρ (♉︎ 13;17°) tomamos el punto opuesto al Sol, dado que es de noche | 31;4º |
| Suma Total (137;14º + 31;4º) | 168;18º |
168;18º es el tiempo de salida (en Clima III - Soene) del horóscopo: ρ (♍︎ 19;51º)
(en el texto: "alrededor de ♍︎ 22 ½º").
Ejemplo 5 - Hallar el punto de la culminación superior según los datos del ejemplo anterior
Desde la mitad hasta el final del Libro II Capítulo 9. Dados los mismos datos como en el Ejemplo 4, hallar el punto de la culminación superior.
Total de horas de estación desde el último mediodía: 6 horas diurnas mas 8 ¼ horas nocturnas.
| Longitud de 1 hora diurna: | 13;22º |
| Longitud de 1 hora nocturna: | 16;38º |
| 6 * 13;22º + 8 ¼ * 16;38º = 80;12º + 137;14º = | 217;26º |
| Tabla de los Tiempos de Salida en la esfera recta del grado del Sol: α (♏︎ 13;17º): | 220;46º |
| Suma total (217;26º + 220;46º): | 78;12º |
El punto de la culminación superior es 78;12º = α (♊︎ 19;11º)
(en el texto: ♊︎ 22 ½º).
| En Suma total realizar el siguiente cálculo: ((Suma total / 360) - Entero(Suma total / 360)) * 360, y todo quedará reducido a un ángulo de un giro (0º a 360º), aquí 78;12º. La Suma total debe estar expresada en un número decimal, entonces: a° + b'/60 + c"/3600. Número de Signo del Zodíaco: Entero(Suma total * 12 / 360), donde 0 es Aries, 1 es Taurus, ..., 11 es Pisces. |
Ejemplo 6 - Hallar el punto de la culminación superior dada la longitud del "horóscopo"
Desde la mitad hasta el final del Libro II Capítulo 9. Dada la longitud del horóscopo en un lugar dado, hallar el punto de culminación superior.
Ejemplo: los mismos datos como en el Ejemplo 4.
| Tiempo de salida del horóscopo en el Clima III (Soene): (♍︎ 19;51º): | 168;18º |
| Menos (-): | 90;0º |
| Diferencia: | 78;18º |
El punto de culminación superior: 78;18º = α (♊︎ 19;16º)
(en el texto:♊︎ 22 ½º).
La discrepancia del resultado con el Ejemplo 5 se debe al redondeo a minutos de las tablas y en cada paso del cálculo.
Ejemplo 7 - Calcular la posición del Sol
Libro III Capítulo 9. Dada la fecha, calcular la posición del Sol.
Ejemplos (cf. Libro IV Capítulo 11 2° eclipse lunar del segundo conjunto de tres eclipses). Fecha: 548° año de la era de Nabonassar, 9/10 de Mechir [VI], 1 ⅓ horas equinocciales después de la medianoche [20 de Marzo de –199].
De la Tabla del Movimiento Medio del Sol:
| Tiempo | Δ seg. λ☉ |
|---|---|
| 540 años | 228;42,48º |
| 7 años | 358;17,53º |
| 150 días | 147;50,43º |
| 8 días | 7;53,6º |
| 13 horas | 0;32,2º |
| 0;20 horas | 0;0,49º |
| Suma total = 547ª 158d 13 ⅓h | 743;17,21º → 23;17,21º |
| más seg. κ (época: 1° de Thoth del 1° año de Nabonassar): | + 265;15º |
| seg. κ: | 288;32,21º |
De la Tabla de la Anomalía del Sol, para el argumento 288;32º, (por interpolación [1]) encontramos la ecuación como de 2;13,28º. Este [valor] es aditivo, dado que κ cae en la segunda columna. Continuando con la tabla anterior.
| κ cae en la segunda columna | 288;32,21º |
| más la longitud del apogeo: | +65;30º |
| seg. λ: | 354;2,21º |
| mas θ | + 2;13,28º |
| λ (la posición del Sol): | 356;15,49º |
| En Suma total realizar el siguiente cálculo: ((Suma total / 360) - Entero(Suma total / 360)) * 360 y todo quedará reducido a un ángulo de un giro (0º a 360º), aquí 23;17,21º. La Suma total debe estar expresada en un número decimal, entonces: a° + b'/60 + c"/3600. Número de Signo del Zodíaco: Entero(λ * 12 / 360), donde 0 es Aries, 1 es Taurus, ..., 11 es Pisces. |
O alrededor de ♓︎ 26;16º
(en el texto: ♓︎ 26;17º).
Fecha y horas calculadas con un programa de computación desde la observación realizada en (Alejandría) de la siguiente:
Nota del traductor al español: datos elaborados con mi software de aplicación “M1 Sistema Astronómico”©. |
Ejemplo 8 - Cálculo de la "ecuación del tiempo"
Al final del Libro III Capítulo 9. Calculo de la "ecuación del tiempo", E (dado un intervalo en días solares verdaderos, hallar el intervalo en días solares medios).
Ejemplo (cf. 1° eclipse lunar del segundo conjunto de tres eclipses Libro IV Capítulo 6):
| tn | Fecha | Hora |
|---|---|---|
| t₁ | 17° año desde Adriano, (880° año de la era Nabonassar), 20/21 de Pauni [X] | 11;15 p.m. (23:15 hs.) |
| t₂ | 19° año desde Adriano, (882° año de la era Nabonassar), 2/3 de Choiak [IV] | 11;00 p.m. (23:00 hs.) |
Desde las tablas solares: Tabla del Movimiento Medio del Sol y Tabla de la Anomalía del Sol (Ver Ejemplo 7 y cf. Manitius I p. 437), [según los datos anteriores]:
| tn | seg. λ(tn) | λ(tn) |
|---|---|---|
| t₁ | ♉︎ 42;21º | 13;15º |
| t₂ | ♎︎ 206;42º | 25;10º |
| Para hallar en seg. λ(tn) el signo del zodíaco: Entero(seg. λ(tn) * 12 / 360), donde 0 es Aries, 1 es Taurus, ..., 11 es Pisces. Nota del traductor al español |
Por consiguiente, en la Tabla de los Tiempos de Salida (en esfera recta) entrando λ(tn) en el signo correspondiente y en la columna "Intervalos de 10°", interpolar [1] con él para hallar el valor en la columna "0° Grados de Tiempo Acumulados":
| α(tn) | Valor Interpolado |
|---|---|
| α (t₁) | 40;44º |
| α (t₂) | 203;17º |
| Δ seg. λ = seg. λ(t₂) - seg. λ(t₁) | Δα = α(t₂) - α(t₁) | Diferencia (Δ seg. λ - Δα ) = E (Ecuación del Tiempo) |
|---|---|---|
| 164;21º | 162;33º | 1;48º = 1;48º / 15 = 7 ⅕ minutos. |
Dado que Δ seg. λ > Δα, restamos E desde el "simple" intervalo de 1 año 166 días 23;45 horas (primera tabla: (t₁ - t₂), en días solares verdaderos), para llegar, al intervalo en días solares medios de: 1 año 166 días 23;37,48 horas
(en el texto: 23 ⅝ horas = 23;37,30 horas).
Libro V Capítulo 9. Para una fecha dada, calcular desde las tablas la latitud y la longitud de la Luna.
Ejemplo: 466° año de la era Nabonassar, 7/8 de Thoth [I], 2 horas equinocciales después de la medianoche (cf. Libro VII Capítulo 3, 4° observación).
De las Tablas de los Movimientos Medios de la Luna:
| seg. λ (Longitud) | seg. α (Anomalía) | seg. ω (Latitud) | seg. η (Elongación) | |
|---|---|---|---|---|
| Valor de la Época (1° de Thoth del 1° año de la era Nabonassar) | 268;49º | 354;15º | 70;37º | |
| 450 años | 260;46,44º | 323;26,5º | 320;54,6º | 10;11,3º |
| 15 años | 140;41,33º | 250;46,52º | 70;41,48º | 144;20,22º |
| 6 días | 79;3,30º | 78;23,24º | 79;22,34º | 73;8,40º |
| 14 horas | 7;41,10º | 7;37,16º | 7;43,2º | 7;6,41º |
| Suma total | 488;12,57º | 929;2,37º | 832;56,30º | 305;23,46º |
| Δ seg. λ = 128;13º | seg. α = 209;3º | seg. ω = 112;56º | 2 * seg. η = 250;48º |
| Para la Suma total en Δ seg. λ, seg. α, seg. ω y 2 * seg. η, realizar el siguiente cálculo: ((Suma total / 360) - Entero(Suma total / 360)) * 360, y todo quedará reducido a un ángulo de un giro (0º a 360º), resultados asignados en la última fila de la tabla anterior. La Suma total debe estar expresada en un número decimal, entonces: a° + b'/60 + c"/3600. Nota del traductor al español |
Desde la Tabla de la Anomalía,
| Pasos | Interpolación / Cálculos |
|---|---|
| Entrar (2 * seg. η) en la columna 1 ó 2 e interpolar [1] en la columna 3 | -13;4º (c₃ = Ecuación del Apogeo) |
| Anomalía verdadera α = seg. α + c₃ | 209;3º - 13;4º = 195;59º |
| Entrar (α) en la columna 1 ó 2 e interpolar en la columna 4 | 1;30º (c₄ = Ecuación Epicíclica) |
| Entrar (α) en la columna 1 ó 2 e interpolar en la columna 5 | 0;55º (c₅ = Incremento Ecuación Epicíclica) |
| Entrar (2 * seg. η) en la columna 1 ó 2 e interpolar en la columna 6 | 0;36,52º (c₆ = Sexagésimas Partes) |
| Ecuación c = c₄ + c₅ * c₆ | +(1;30º + 0;55º * 0;36,52º) = +2;4º |
| Longitud λ = Δ seg. λ + c + λ(época) | 128;13º + 2;4º + 41;22º = 171;39º (en el texto: 171;30º). |
| ω = seg. ω + c | 112;56º + 2;4º = 115;0º |
| Entrar (ω) en la columna 1 ó 2 e interpolar en la columna 7: Latitud β(ω) | -2;7º (c7 = Latitud) (en el texto: -2 ⅙º) |
Datos calculados con un programa de computación desde la observación realizada por Timocares (actual Alejandría) de la:
Nota del traductor al español: carta y datos elaborados con mi software de aplicación “M1 Sistema Astronómico”©. |
Ejemplo 10 - Dado un instante y lugar, con las tablas, calcular la paralaje lunar con la longitud lunar y solar, la latitud lunar y su elongación
Libro V Capítulo 19. Calcular la paralaje Lunar con la longitud lunar y solar, latitud lunar y su elongación.
Ejemplo: instante (tiempo), 2 ½ horas equinocciales después de la medianoche (tiempo local verdadero de Alejandría); λ☉: ♏︎ 13;17º; λ☽︎: ♍︎ 21;30º, β☽︎: -2 ⅙º (cf. Libro VII Capítulo 3, 4° observación) y Ejemplo 9).
Con la longitud solar y el tiempo local: el punto de culminación: ♊︎ 19;11º (cf. Ejemplo 5).
Distancia de la Luna desde el meridiano [(de Alejandría)]:
α (♍︎ 21;30º) - α (♊︎ 19;11º) = 172;12º - 78;12º = 94º = 6;16 horas al Este (06:16 hs.).
Desde las Tablas de los Ángulos y de los Arcos (Clima III, Bajo Egipto), argumentos: 6;16 horas ("Hora", vertical) y 21;30º (horizontal), por interpolación [1] en las tablas de Virgo y Libra:
| arco | 90º |
| ángulo Este | 172;30º |
Corrección del arco y del ángulo de la latitud lunar (cf. Libro V Capítulo 19 Fig. 5.20) y según la Tabla de las Cuerdas:
| Cuerda (2 * (180º - 172;30º)) = Cuerda 15º | 15;40p |
| Cuerda (180º - 15º) = Cuerda 165º | 118;58p |
Multiplicando β☽︎ 2 ⅙° (+) en cada uno de ellos y dividiéndolos por 120, nos da 0;17º y 2;9º respectivamente.
| 2 ⅙° * 15;40p / 120p | 0;17º |
| 2 ⅙° * 118;58p / 120p | 2;9º |
Entonces el arco corregido esta dado por
| ((90º + 0;16º) ^ 2 + (2;9º) ^ 2)) ^ 0,5 | ≈ 90;18º |
Y el ángulo correspondiente de la corrección de:
| 2;9º * 120p / 90;18º | 2;51p |
que es la cuerda cerca de los 2;44º (ver Tabla de las Cuerdas), cuya mitad es 1;22º.
Por lo tanto el ángulo corregido es de
| 172;30º - 1;22º | 171;8º |
Tomamos el arco como de exactamente 90º (dado que de otro modo la Luna podría estar debajo del horizonte).
CÁLCULO DE LA PARALAJE LUNAR TOTAL
Según el Ejemplo 9, la anomalía verdadera lunar α☽︎ = 195;59º y la elongación lunar seg. η = 305;24º.
La paralaje lunar:
Desde la Tabla de la Paralaje, entrando con el argumento ζ = 90º.
| 3º Columna | 4º Columna | 5º Columna | 6º Columna |
|---|---|---|---|
| 0;53,34 | 0;10,17 | 1;19,0 | 0;25,0 |
| Con el argumento (360º - α☽︎) / 2 | interpolar [1] en la 7° Columna | interpolar en la 8° Columna |
|---|---|---|
| ~ 82º | 58,39 | 58,31 |
| Paralaje en la sizigia: | 0;53,34 + 0;10,17 * 0;58,39 | 1;3,37º |
| Paralaje en la cuadratura: | 1;19,0 + 0;25,0 * 0;58,31 | 1;43,23º |
| Diferencia Δ: | 0;39,46º |
| Con el argumento (360º - seg. η) | interpolar [1] en la 9° Columna |
|---|---|
| 360º - 305;23,46º = 54;36º | 42;35 |
Paralaje lunar total: 1;3,37º + 0;39,46º * 0;42,35º ≈ 1;32º.
DETERMINACIÓN DE LOS COMPONENTES LONGITUDINALES Y LATITUDINALES DE LA PARALAJE
El ángulo entre el círculo horario y la eclíptica (ver más arriba, el ángulo corregido): 171;8º. Este es mayor que 90º, así que tomamos su ángulo suplementario de 171;8º = 180º - 171;8º = 8;52º. Dos veces esto (8;52º * 2) = 17;44º, y de esto último su ángulo suplementario 162;16º.
Según la Tabla de las Cuerdas
| Ángulo [1] | Cuerda Interpolada |
|---|---|
| 17;44º | 18;30p |
| 162;16º | 118;34p |
| Tipo de Paralaje | Cálculo | Paralaje |
|---|---|---|
| Latitudinal | 1;32º * 17;44º / 120p | ≈ 0;13 ½º |
| Longitudinal | 1;32º * 118;34º / 120p | ≈ 1;31º |
La paralaje latitudinal es hacia el Sur (el cenit al Norte del punto de culminación).
Dado que la paralaje latitudinal es hacia el Sur y el ángulo es mayor que 90º, la paralaje longitudinal es positiva.
Resultado:
Paralaje en latitud: -0;13 ½º (en el texto: -0;5º).
Paralaje en longitud: +1;31º (en el texto: +1;0º).
Ejemplo 11 - Cálculo de un eclipse de Luna
Libro VI Capítulo 9. Dado el año y mes, calcular un eclipse lunar.
Ejemplo: Fecha: Año: 28° año de Nabonassar, Mes: Thoth, (cf. Libro IV Capítulo 6. De los tres primeros más antiguos, el segundo eclipse lunar, ocurrido en el segundo año del mismo Mardokempad, 18/19 de Thoth [I] en el calendario Egipcio [8/9 de Marzo –719]).
En las Tablas de las Conjunciones y de las Oposiciones, calcular la oposición media (fase lunar: llena):
| Período | Días de Thoth | seg. κ (Distancia del Sol) | seg. α (Anomalía) | seg. ω (Latitud) |
|---|---|---|---|---|
| En la Tabla de las Oposiciones, 26 años: | 9;55,35 días | 267;58,12º | 83;24,29º | 230;10,5º |
| En la Tabla Incrementos Anuales y Mensuales (Oposición y Conjunción)), año: 2° | 8;15,53 días | 7;39,36º | 285;25,4º | 46;45,54º |
| Suma total: 28 años | 18;11,28 días | 275;37,48º | 8;49,33º | 276;55,59º |
| Para la Suma total en cada columna, realizar el siguiente cálculo: ((Suma total / 360) - Entero(Suma total / 360)) * 360, y todo quedará reducido a un ángulo de un giro (0º a 360º), resultados asignados en la última fila de la tabla anterior. La Suma total debe estar expresada en un número decimal, entonces: a° + b'/60 + c"/3600. Tiempo de la oposición media: |
Tiempo de la oposición media: 18;11,28 días de Thoth a las 4;35 p.m. (16:35 hs.).
| Comprobar con Seg. ω si hay eclipse lunar o no, según en la descripción en la tabla "LÍMITES [DEL ECLIPSE] DE LA LUNA EN EL MOVIMIENTO MEDIO [LATITUDINAL]" que van desde 74;48º a 105;12º y desde 254;48º a 285;12º. Nota del traductor al español |
Seg. ω (276;55,59º) cae dentro de los límites de la eclíptica para el eclipse lunar, por lo tanto es posible [tal eclipse].
CÁLCULO DE LA OPOSICIÓN VERDADERA
| Interpolar con el argumento [1] | Valor Interpolado |
|---|---|
| c(seg. κ) = 275;37,48º en la Tabla de la Anomalía del Sol: | +2;21º (Ecuación solar) |
| c(seg. α) = 8;49,33º en la Tabla de la primera Anomalía simple de la Luna: | -0;42º (Ecuación lunar) |
| Verdadera posición en latitud: ω = seg ω + c(seg. α) = 276;14º en la oposición media |
| Δλ = 2;21º + 0;42º = 3;3º |
| Movimiento horario verdadero de la Luna en longitud: 0;32,56º - 0;32,40º * 4 ⅔' = 0;30,24º |
| Δt = 3;3º * (13/12) / 0;30,24º = 6;31 horas (06;31 hs.) |
La longitud verdadera de la Luna en la Sizigia media es menor que la longitud verdadera del Sol (menos 180º). Así que sumamos Δt al tiempo de la oposición media para que nos de el tiempo de la oposición verdadera igual a 11;6 p.m. (en el texto: 11;10 p.m., 23:00 hs.).
Movimiento en Δt = 3;3º * (13/12) = 3;18º.
Sumamos este movimiento a la posición verdadera en latitud, ω = ω + Δt = 276;14º + 3;18º = 279;32º en la oposición verdadera.
En 6;31 horas el movimiento [medio] en anomalía es de 3;33º, entonces en la oposición verdadera seg. α = seg. α + 3;33º = la (Anomalía) = 12;22º.
CÁLCULO DE LAS CIRCUNSTANCIAS DEL ECLIPSE LUNAR
Desde la Tabla de los Eclipses, en la "Tabla Eclipses Lunares":
| Interpolar con el Agumento [1] | Magnitud interpolada | Duración interpolada (Minutos de Inmersión) |
|---|---|---|
| 279;32º | 2;32 dígitos | 0;26,22º |
| Interpolar con el Argumento [1] | Magnitud interpolada | Duración interpolada (Minutos de Inmersión) |
|---|---|---|
| 279;32º | 4;42 dígitos | 0;39,35º |
| Diferencia | Mag. Dist. Mayor - Mag. Dist. Menor | Dura. Dist. Mayor - Dura. Dist. Menor |
|---|---|---|
| Δ | 2;10 dígitos | 0;13,13º |
Desde la Tabla de los Eclipses, en la "Tabla de Corrección - Tabla de Magnitudes":
| Interpolar con el argumento seg α [1] | Sexagésimas interpoladas (Tabla de Corrección) | Magnitud | Duración |
|---|---|---|---|
| 12;22º | 0;43º | 2;32 dígitos + 2;10 dígitos * 0;0,43º = 2;34 dígitos (en el texto: 3 dígitos observados) | 0;26,22º + 0;13,13º * 0;0,43º = 0;26,31º |
Para obtener el tiempo desde el comienzo hasta el eclipse medio, dividimos la duración (de 0;26,31º incrementada por una duodécima parte), dividido por el movimiento horario verdadero de la Luna:
| Tiempo desde el Comienzo del Eclipse hasta el Eclipse Medio |
|---|
| 0;26,31º * (13/12) / 0;30,24º = 0;57 horas |
| Fase del Eclipse | Tiempo |
|---|---|
| Comienzo del eclipse | 10;9 p.m. (22:09 hs. del 18 de Thoth) |
| Eclipse medio | 11;6 p.m. (23:06 hs. del 18 de Thoth) |
| Fin del eclipse | 12;3 a.m. (00:03 hs. del 19 de Thoth) |
| Fecha y horas calculadas con un programa de computación desde la observación realizada por los Babilonios (actual Bagdad) del siguiente:
Nota del traductor al español: carta y datos elaborados con mi software de aplicación “M1 Sistema Astronómico”©. |
Ejemplo 12 - Cálculo de un eclipse de Sol
Libro VI Capítulo 10. Dado el año, mes y lugar, calcular un eclipse solar.
En el Almagesto no hay ejemplos de eclipses solares, así que he seleccionado el Eclipse del 16 de Junio de 364 d.C., que Teón observó en Alejandría, y dado como ejemplo de cálculo en su comentario sobre el Almagesto, primero de acuerdo al Almagesto, y nuevamente de acuerdo a las Tablas Manuales o Prácticas (Edición de Basilea pp. 332 - 339, cf. Rome [6]). Un cálculo algo diferente del mismo eclipse también aparece en algunos manuscritos en el breve comentario de Teón sobre las 'Tablas Manuales o Prácticas, y ha sido publicado in extenso por Anne Tihon [en su obra] "Calcul de l'eclipse".
Ejemplo: Fecha: Año: 1112° año de Nabonassar, Mes: Thoth, Lugar: Alejandría.
En las Tablas de las Conjunciones y de las Oposiciones, calcular la conjunción media (fase lunar: nueva):
| Período | Días de Thoth | seg. κ (Distancia del Sol) | seg. α (Anomalía) | seg. ω (Latitud) |
|---|---|---|---|---|
| En la Tabla de las Conjunciones, 1101 años: | 22;41,45 días | 19;11,56º | 222;53,32º | 65;41,57º |
| En la Tabla Incrementos Anuales y Mensuales (Oposición y Conjunción)), 11 años: | 1;9,39 días | 358;28,11º | 271;4,19º | 211;12,3º |
| Suma Total: 1112 años | 23;51,24 días | 17;40,7º | 133;57,51º | 276;54,0º |
| Para la Suma total en cada columna, realizar el siguiente cálculo: ((Suma total / 360) - Entero(Suma total / 360)) * 360, y todo quedará reducido a un ángulo de un giro (0º a 360º), resultados asignados en la última fila de la tabla anterior. La Suma total debe estar expresada en un número decimal, entonces: a° + b'/60 + c"/3600. Tiempo de la conjunción media: |
Tiempo de la oposición media: 23;51,24 días de Thoth a las 8;34 a.m. (08:34 hs.).
| Comprobar con seg. ω si hay eclipse solar o no, según en la descripción en la tabla "LÍMITES [DEL ECLIPSE] DEL SOL EN EL MOVIMIENTO MEDIO [LATITUDINAL]" que van desde 69;19º a 101;22º y desde 258;38º a 290;41º. Nota del traductor al español |
Seg. ω (276;54,0º) cae dentro de los límites de la eclíptica para el eclipse solar, por lo tanto es posible [tal eclipse].
CÁLCULO DE LA CONJUNCIÓN VERDADERA
| Interpolar con el argumento [1] | Valor Interpolado |
|---|---|
| c(seg. κ) = 17;40,7º en la Tabla de la Anomalía del Sol: | -0;41º (Ecuación solar) |
| c(seg. α) = 133;57,51º en la Tabla de la primera Anomalía simple de la Luna: | -3;50º (Ecuación lunar) |
| Verdadera posición en latitud: ω = seg ω + c(seg. α) | 273;4º en la conjunción media |
| Δλ = -0;41º + 3;50º | 3;9º |
| Movimiento horario verdadero de la Luna en longitud: 0;32,56º - 0;32,40º * 3 ⅔' | 0;34,56º (Teón: 0;34,56º) |
| Δt = 3;9º * (13/12) / 0;34,56º | 5;52 horas |
El tiempo de la conjunción verdadera: 8;34 a.m. + 5;52 horas = 2;26 p.m. (Teón: 2 + ⅓ + 1/10 horas después del mediodía).
Movimiento en Δt = 3;9º * (13/12) = 3;25º.
Sumamos este movimiento a la posición verdadera en latitud, ω = ω + Δt = 273;4º + 3;25º = 276;29º en la conjunción verdadera.
En 5;52 horas el movimiento medio en anomalía es de 3;12º, entonces en la conjunción verdadera seg. α = seg. α + 3;12º = la (anomalía) 137;10º.
Para hallar en Alejandría el tiempo de la conjunción aparente primero tenemos que hallar el tiempo local verdadero, por ej. aplicar la ecuación del tiempo (Ejemplo 8).
| Longitud verdadera del Sol en la conjunción media: | seg. κ + seg. λₐ + c(seg. κ) | 17;40º + 65;30º - 0;41º | 82;29º |
| Movimiento del Sol desde la conjunción media hasta la verdadera: | Δλ / 12 | 3;9º / 12 | 0;16º |
| Longitud verdadera del Sol en la conjunción verdadera: | seg. κ + seg. λₐ + c(seg. κ) + Δλ / 12 | 82;29º + 0;16º | 82;45º |
Por consiguiente la ecuación de tiempo con respecto a la era de Nabonassar (cf. Ejemplo 8 para el método [a aplicar]): +24 minutos.
Tiempo de la conjunción verdadera con respecto al mediodía en Alejandría: 2;50 p.m.
CÁLCULO DE LA CONJUNCIÓN APARENTE
(1) CÁLCULO DE LA PARALAJE LUNAR (cf. Ejemplo 10):
Desde las Tablas de los Ángulos y de los Arcos Propuestos, Clima III (Bajo Egipto), interpolar [1] con los argumentos longitud del Sol λ☉ y tiempo de la conjunción verdadera (tiempo local)
| Longitud del Sol λ☉ | Tiempo de la Conjunción Verdadera (Tiempo Local) | Distancia Cenital | Ángulo |
|---|---|---|---|
| ♊︎ 22;45º | 2;50 p.m. (14:50 hs.) | 38;28º | 17;35º |
Desde la Tabla de la Paralaje, interpolar [1] con el argumento ζ
| ζ | Anomalía Lunar Verdadera α☽︎ | Paralaje Total del Sol | Paralaje Total de la Luna (solo 3º y 4º columnas) | Diferencia en las Paralajes |
|---|---|---|---|---|
| 38;28º | 137;10º (la latitud lunar es obviada) | 0;1,45º | 0;39,35º | 0;39,35º - 0;1,45º = 0;37,50º. |
Paralaje longitudinal (para el ángulo 17;35º): pλ = 0;36º.
El tiempo desde la conjunción verdadera hasta la aparente es hallada dividiendo [el resultado] anterior por la velocidad horaria verdadera de la Luna: 0;36º / 0;34,56º ≈ 1;2 horas.
Por consiguiente, el tiempo de la conjunción aparente (primera aproximación): 3;52 p.m. (15:52 hs.)
(2) SEGUNDO CÁLCULO DE LA PARALAJE LUNAR, para el tiempo corregido:
Desde las Tablas de los Ángulos y de los Arcos Propuestos, Clima III (Bajo Egipto), interpolar [1] con los argumentos Longitud del Sol λ☉ y Tiempo de la Conjunción Verdadera (Tiempo Local)
| Longitud del Sol λ☉ | Tiempo de la Conjunción Verdadera (Tiempo Local) | Distancia Cenital | Ángulo |
|---|---|---|---|
| ♊︎ 22;45º | 3;52 p.m. (15:52 hs.) | 51;48º | 18;32º |
En 1;2 horas el movimiento medio en anomalía es alrededor de 0;33º, por consiguiente seg. α para el tiempo corregido es de seg. α = seg. α + 0;33º = 137;10º + 0;33º = la (Anomalía) 137;43º.
Sin tener en cuenta la latitud lunar, como [se hizo] anteriormente, desde la Tabla de la Paralaje, interpolar [1] con el argumento ζ
| ζ | Anomalía Lunar Verdadera α☽︎ | Paralaje Total del Sol | Paralaje Total de la Luna (solo 3º y 4º columnas) | Diferencia en las Paralajes |
|---|---|---|---|---|
| 51;48º | 137;43º (la latitud lunar es obviada) | 0;2,15º | 0;49,47º | 0;49,47º - 0;2,15º = 0;47,32º. |
Paralaje longitudinal (para el ángulo 18;32ºº): p'λ = 0;45º.
(3) CÁLCULO DE LA "EPIPARALAJE" [o diferencia entre la primera y la segunda paralaje]:
Diferencia entre la primera (1) y la segunda paralaje longitudinal (2),
| p'λ - pλ | d (diferencia) |
|---|---|
| 0;45º - 0;36º | 0;9º |
| hallar f (incremento) desde f / d = d / p | f | Epiparalaje = (d + f) | Paralaje Final en Longitud |
|---|---|---|---|
| 0;9º * 0;9º / 0;36º | ≈ 0;2 | 0;11º | 0;36º + 0;11º = 0;47º |
Para tener en cuenta el movimiento del Sol sumar 1/12 ma. parte a este: (13 / 12) * 0;47º ≈ 0;51º.
Tiempo desde la conjunción verdadera hasta la aparente: 0;51º / 0;34,56º ≈ 1;28 horas.
Por consiguiente el tiempo de la conjunción aparente: 2;50 horas + 1;28 horas = 4;18 p.m. (Teón: 4 ⅓ horas p.m., 16:20 hs.)
(4) POSICIÓN DE LA LUNA EN ESE INSTANTE:
| λ | ♊︎ 22;45º + 0;51º | ♊︎ 23;36º |
| ω | 276;29º + 0;51º | 277;20º |
| α | 137;10º + 0;51º | 138;1º |
CÁLCULO DE LAS CIRCUNSTANCIAS DEL ECLIPSE SOLAR (PARCIAL)
CÁLCULO DE LA PARALAJE LATITUDINAL:
Desde las Tablas de los Ángulos y de los Arcos Propuestos, Clima III (Bajo Egipto), interpolar [1] con los argumentos de la longitud del Sol λ☉ y el tiempo de la conjunción verdadera (tiempo local)
| Longitud del Sol λ☉ | Tiempo de la Conjunción Verdadera (Tiempo Local) | Distancia Cenital | Ángulo |
|---|---|---|---|
| ♊︎ 23;36º2 | 4;18 p.m. | 57;18º | 19;46º |
Sin tener en cuenta la latitud lunar, como [se hizo] anteriormente, desde la Tabla de la Paralaje, interpolar [1] con el argumento ζ
| ζ | Anomalía Lunar Verdadera α☽︎ | Paralaje Total del Sol | Paralaje Total de la Luna (solo 3º y 4º columnas) | Diferencia en las Paralajes |
|---|---|---|---|---|
| 57;18º | 138;1º (la latitud lunar es obviada) | 0;2,24º | 0;53,2º | 0;53,2º - 0;2,24º = 0;50,38º. |
La paralaje latitudinal (cf. Ejemplo 10) para el ángulo 19;46º: pβ = 0;17º.
Convertimos esto para una distancia a lo largo de la órbita lunar, multiplicándolo por 12:
Δω = 12 * pβ = 3;24º (Teón utiliza el factor 11 ½ y le da 3;19º).
Dado que ω es 277;20º, la Luna esta pasando justamente por el nodo ascendente (☊). El efecto de la paralaje es hacia el Sur, por lo tanto su efecto sobre ω es negativo.
La posición final de la Luna sobre su órbita es : 277;20º - 3;24º = 273;56º, que es el argumento aparente de la Latitud.
Desde las Tablas de los Eclipses, interpolar [1] con el argumento de la latitud aparente de la Luna β☽︎ = 273;56º
| Magnitud (dígitos) | Duración [minutos de recorrido] |
|---|---|
| 4;8 | 23;44,28 |
| Magnitud (dígitos) | Duración [minutos de recorrido] |
|---|---|
| 4;56 | 26;18,52 |
| Magnitud (dígitos) | Duración [minutos de recorrido] |
|---|---|
| 0;48 | 2;34,24 |
Desde las Tablas de Corrección, interpolar [1] con el argumento α = 138;1º
| Sexagésimas [partes] interpolada | Magnitud (dígitos) | Duración [minutos de recorrido] |
|---|---|---|
| 51,39 | 4;8 + 0;48 * 0;51,39 = 4;49º | 23;44,28 + 2;34,24 * 0;51,39 = 25;57 |
Incrementamos esto último por 1/12 ma. parte, para tener en cuenta el movimiento del sol: 28;7',
y dividirlo por la velocidad horaria de la Luna, 0;34,56º, para tomar la duración media del eclipse: 0;28,7 / 0;34,56 ≈ 0;48,18 horas (Teón: ½ + ¼ + 1/20 = 0;48 horas).
Por lo tanto las circunstancias del eclipse (sin considerar la variación de la distancia cenital durante el eclipse):
| Fase | Hora | Según Teón |
|---|---|---|
| Comienzo del eclipse - 1° contacto Luna-Sol | 3;30 p.m. (15:30 hs.) | 3;32 p.m. (15:32 hs.) |
| Eclipse medio | 4;18 p.m. (16:18 hs.) | 4;20 p.m. (16:20 hs.) |
| Fin del eclipse - último contacto Luna-Sol | 5;6 p.m. (17:06 hs.) | 5;8 p.m. (17:08 hs.) |
(Teón pasa a calcular las diferencias en el comienzo y en el final del eclipse debido a la variación en la distancia cenital, cf. desde la mitad hasta el final del Libro VI Capítulo 10. Estas cantidades son de 12 minutos mas temprano y de 7 minutos mas tarde respectivamente, verificando los pasos de Ptolomeo acerca del efecto en los intervalos).
Utilizando unas tablas más modernas (aquellas de Paul Viktor Neugebauer, en Astonomische Chronologie), encuentro:
| Fase | Hora |
|---|---|
| Comienzo del eclipse - 1° contacto Luna-Sol | 15;18 hs. |
| Eclipse medio | 16;28 hs. |
| Fin del eclipse - último contacto Luna-Sol | 17;24 hs. |
Fecha y horas calculadas con un programa de computación desde la observación realizada por Teón (en Alejandría) del siguiente:
Nota del traductor al español: datos elaborados con mi software de aplicación “M1 Sistema Astronómico”©. |
Ejemplo 13 - Calcular la "inclinación" desde el horizonte hasta el 1° contacto del limbo lunar con el limbo solar
Libro VI Capítulo 13. Dadas las circunstancias de un eclipse (magnitud y horas de las fases principales), calcular la "inclinación" (, por ej. el punto en el horizonte hacia el que apunta la línea que une los centros [de la Luna y el Sol]).
Tomamos como ejemplo el eclipse solar del Ejemplo 12 (16 Junio 364 d.C. = 24 de Thoth de 1112° de la era Nabonassar, observado por Teón), al comienzo del eclipse (1° contacto limbo lunar - limbo solar).
Dado el instante (tiempo) en Alejandría, 3;30 p.m.; magnitud, 4;49 dígitos. Primero, hallar el punto de salida de la eclíptica (cf. Ejemplo 4).
La longitud del Sol es ♊︎ 22;45º (cf. Ejemplo 12).
Tiempo en horas de estación en Alejandría: 3 horas después del mediodía (cf. Ejemplo 2).
Por consiguiente el punto de salida de la eclíptica es: ♏︎ 10º; y por lo tanto el punto de la puesta es ♉︎ 10º.
En la Fig. 6.7, azimut de ♉︎ 10º en Clima III (Bajo Egipto): (click en la imagen para aumentar)
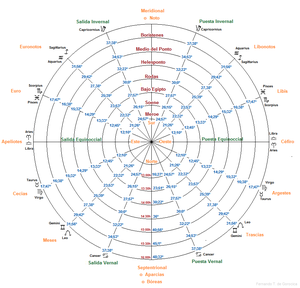
| Grados Signo Zodíaco | Azimut |
|---|---|
| ♉︎ 0º | 13;33º hacia el Norte desde el Oeste (103;33°) |
| ♊︎ 0º | 23;53º hacia el Norte desde el Oeste (113;53°) |
| Por lo tanto ♉︎ 10º | 17º hacia el Norte desde el Oeste (107°) |
En la Tabla de Visualización de los diagramas de las Inclinaciones, interpolar [1] con el argumento 4;49 dígitos en la 2° columna
| argumento [dígitos] | SOL: comienzo y fin eclipse (interpolado) |
|---|---|
| 4;49 | 37;41º |
La Luna esta al Norte de la eclíptica (en el Ejemplo 12 la posición en latitud ω es un poco más que 270º).
Por consiguiente este ángulo esta ubicado al Norte del punto de la puesta.
Entonces el punto de "inclinación" sobre el Horizonte esta en = 17º + 37;41º = 54;41º hacia el Norte desde el Oeste (144° 41').
Ejemplo 14 - Calcular la longitud de un planeta
Libro XI Capítulo 12. Dado un instante calcular la longitud de un planeta desde las Tablas de los Movimientos Medios en Longitud y en Anomalía de los cinco Planetas.
Ejemplo: Planeta: Marte, Instante: a las 9 p.m. (21:00 hs.) del 15/16 de Epiphi de 886° de Nabonassar o 30/31 de Mayo de 139 d.C. (cf. Libro X Capítulo 8, donde Marte es observado en ese momento).
En las Tablas de los Movimientos Medios en Longitud y en Anomalía de los cinco Planetas, hallar la longitud media y anomalía media:
| Tiempo | seg. λ | seg. α |
|---|---|---|
| Época (1 de Thoth de 1° de la era Nabonassar) | 3;32º | 327;13º |
| 810 años | 138;15,13º | 24;48,59º |
| 72 años | 92;17,21º | 250;12,21º |
| 3 años | 213;50,43º | 145;25,31º |
| 10 meses (300 días) | 157;13,4º | 138;28,21º |
| 14 días | 7;20,13º | 6;27,43º |
| 9 horas | 0;11,47º | 0;10,23º |
| Suma total: 885 años 314 días 9 horas | 612;40,21º | 892;46,18º |
| Por consiguiente | 252;40º | 172;46º (como en el Libro X Capítulo 8) |
| En Suma total realizar el siguiente cálculo en seg. λ y en seg. α : ((Suma total / 360) - Entero(Suma total / 360)) * 360, y todo quedará reducido a un ángulo de un giro (0º a 360º), aquí 78;12º. Ambas sumas seg. λ y seg. α deben estar expresadas en un número decimal, entonces: a° + b'/60 + c"/3600. Nota del traductor al español |
Posición del apogeo en la época (Nabonassar): ♋︎ 16;40º
Movimiento del apogeo en 886 años (1º en 100 años): 8;52º
Por consiguiente la posición del apogeo en la fecha: 115;32º.
Centrum medio (seg. κ): 252;40º - 115;32º = 137;8º (Libro X Capítulo 8: 137;11º).
Desde las Tablas para determinar las Posiciones en Longitud de los cinco Planetas:
con el argumento seg. κ, hallar la ecuación del centro interpolando [1] desde la 3° y 4° columna ("Ecuación en Longitud" y "Diferencia en la Ecuación"):
| con el argumento seg. κ [1] | "Ecuación en Longitud" interpolada | "Diferencia en la Ecuación" interpolada | Suma |
|---|---|---|---|
| 137;8º | 9;3 | -0;41 | 9;3º + (-0;41º) = 8;22º (cf. Libro X Capítulo 8, el ^ ZBE = 16;44ºº) |
Dado que seg. κ esta en la primera columna (por ser menor que 180º), restamos [el último resultado] a seg. λ y lo sumamos a seg. α:
| λ' | α |
|---|---|
| 252;40º - 8;22º = 244;18º | 172;46º + 8;22º = 181;8º |
| con el argumento [1] | 6° columna: "Ecuación de la Anomalía" interpolada (C₆) |
|---|---|
| α = 181;8º | 2;10º |
| con el argumento [1] | 8° columna: "Sexagésimas" interpolada (C₈) |
|---|---|
| seg. κ = 137;8º | 37,9 |
Dado que el seg. κ esta entre la distancia media y el perigeo (positivo en la 8° columna),
| con el argumento [1] | 7° columna: "Diferencia Aditiva" interpolada (C₇) |
|---|---|
| 181;8º | 0;53º |
Entonces
| Ecuación de la Anomalía (C) | Cálculo | Resultado = C |
|---|---|---|
| C₆ + C₈ * C₇ | 2;10º + 0;53º * 0;37,9º | 2;43º (cf. Libro X Capítulo 8, el ^ BEX = 5;26ºº) |
Dado que α es mayor que 180º (en la 2° columna del argumento), esta ecuación es negativa, por lo tanto
| Longitud del Planeta λ | Cálculo | Resultado = λ |
|---|---|---|
| λ' - c | 244;18º - 2;43º | 241;35º (en el Libro X Capítulo 8 observado: ♐︎ 1 ⅗º). |
| En λ realizar el siguiente cálculo: ((λ / 360) - Entero(λ / 360)) * 360 y todo quedará reducido a un ángulo de un giro (0º a 360º), aquí 241;35º. La λ debe estar expresada en un número decimal, entonces: a° + b'/60 + c"/3600. Número de Signo del Zodíaco: Entero(λ * 12 / 360), donde 0 es Aries, 1 es Taurus, ..., 11 es Pisces. |
| Fecha y horas calculadas con un programa de computación desde la observación realizada por Ptolomeo (actual Alejandría) de la siguiente:
Nota del traductor al español: cartas y datos elaborados con mi software de aplicación “M1 Sistema Astronómico”©. |
Ejemplo 15 - Calcular la latitud de un planeta
Libro XIII Capítulo 6. Calcular la latitud del planeta, dada la "longitud corregida" (ver en Libro XIII Capítulo 6, nota de Referencia nro. 2: κ₀, la distancia del centro del Epiciclo desde el apogeo) y la "anomalía corregida" (α).
(a) PARA UN PLANETA EXTERIOR:
Ejemplo: Júpiter, a las 6 a.m. del 18 de Epiphi de 507° de la era Nabonassar (cf. Libro XI Capítulo 3, 4 de Septiembre de 240 a. C.).
Dados: κ₀ = 290;40º, α = 72;3º.
En las Tablas para los Cálculos en Latitud
| con el argumento [1] | en la 5° columna: "sexagésimas" interpolada C₅(ω) |
|---|---|
| ω = κ₀ - 20º = 270;40º | 0;43 |
Si ω > 270º, entonces
| con el argumento [1] | en la 3° columna: "límite Norte" interpolada C₃(α) |
|---|---|
| α = 72;3º | 1;21º |
| Latitud del Planeta β | Cálculo | Resultado ~ β |
|---|---|---|
| β = C₃ * C₅ | 1;21º * 0;0,43º | ~ +0;1º (al Norte ya que tomamos C₃) |
El texto dice que Júpiter ocultó a δ Cancer, que de acuerdo con el catálogo de estrellas (Constelación XXV Estrella nro. 5) esta tiene una longitud de -0 ⅙º. Por consiguiente hay una discrepancia de ⅙º. Bryant Tuckerman en su obra "Planetary, Lunar and Solar Positions" para el 4 de Septiembre de 240 a. C. (-241) da β ≈ +0;14º. Dado que δ Cancer, por cálculos modernos, estuvo exactamente sobre la eclíptica en el momento de la observación, no pudo haber ocurrido una ocultación.
Efeméride calculada con un programa de computación desde la observación realizada por Dionysius (actual Atenas) de la siguiente:
Nota del traductor al español: datos elaborados con mi software de aplicación “M1 Sistema Astronómico”©. |
(b) PARA UN PLANETA INTERIOR:
Ejemplo: Mercurio, a las 6 a.m. del 18 de Choiac de 486° de Nabonassar (cf. Libro IX Capítulo 7, [5] observación, 11/12 de Febrero de 261 a. C.).
Dados: κ₀ = 129;44º, α = 239;15º.
En las Tablas para los Cálculos en Latitud
| con el argumento [1] | en la 3° columna: "Inclinación" interpolada (C₃) |
|---|---|
| α = 239;15º | 1;27º |
| con el argumento [1] | en la 4° columna: "Oblicuidad" interpolada (C₄) |
|---|---|
| α = 239;15º | 2;29º (*) |
(*) Dado que 90º < κ₀ < 270º, adicionamos a estos últimos (2;29º) la 1/10 ma. parte de sí mismo, entonces:
| "Oblicuidad" corregida (C₄') |
|---|
| 2;29º + 0;15º = 2;44º |
| con el argumento [1] κ' = κ₀ + 270º | en la 5° columna: "Sexagésimas" interpolada C₅(κ') |
|---|---|
| κ' = 39;44º | 45,55 |
| C₃ * C₅ | β1 |
|---|---|
| 1;27º * 0;45,55º | 1;7º |
La condición A2 (Libro XIII Capítulo 6) sostiene, dado que κ' < 90º, 90º < α < 270º, entonces β₁ esta al Norte.
| con el argumento [1] κ" = κ₀ + 180º | en la 5° columna: "Sexagésimas" interpolada C₅(κ") |
|---|---|
| κ" = 309;44º | 38;11 |
| C₄' * C₅' | β₂ |
|---|---|
| 2;44º * 0;38,11º | 1;44º |
La condición A2 (Libro XIII Capítulo 6) sostiene, dado que 270° < κ" < 360º, α > 180º, entonces β₂ esta al Sur.
| C₅ * C₅' * C₅' | β₃ |
|---|---|
| 0;45,55º * 0;38,11º * 0;38,11º | 0;18º (Este esta al Sur) |
| β₁ + β₂ + β₃ | Latitud del Planeta β |
|---|---|
| +1;7º - 1;44º - 0;18º | -0;55º |
El texto dice que Mercurio estuvo a "3 Lunas hacia el Norte" de δ Capricornus. En el catálogo de estrellas (Constelación XXXI Estrella nro. 24) esta tiene una latitud de -2º; entonces de acuerdo a la observación de la latitud de Mercurio, debería ser de -½º, una discrepancia en los cálculos de alrededor de ½º.
Bryant Tuckerman en su obra "Planetary, Lunar and Solar Positions" para el 12 de Febrero de 261 a. C. (-261), 6 a.m., Alejandría, encuentro una latitud de alrededor de +0;8º.
Fecha y horas calculadas con un programa de computación desde la observación realizada en (Alejandría) de la siguiente:
Nota del traductor al español: datos elaborados con mi software de aplicación “M1 Sistema Astronómico”©. |
Ejemplo 16 - ¿Como derivó Ptolomeo los movimientos medios para los cinco planetas?
Nuestra discusión solamente concierne a los movimientos medios diarios en anomalía, dado que los movimientos medios Diarios en longitud no son derivados independientemente: para Venus y Mercurio los últimos son idénticos con aquellos del Sol, mientras que para los planetas exteriore son encontrados restando los movimientos medios diarios en anomalía con el movimiento medio diario del Sol.
La respuesta a la pregunta de arriba podría ser provista por aquellos capítulos titulados, "Sobre la Corrección de los Movimientos Periódicos [de cada Planeta]" en el: Libro IX Capítulo 10 para (Mercurio), Libro X Capítulo 4 para (Venus), Libro X Capítulo 9 para (Marte), Libro XI Capítulo 3 para (Júpiter) y Libro XI Capítulo 7 para (Saturno). En cada caso, Ptolomeo determina la posición del planeta en el Epiciclo en una de sus propias observaciones, y también en una observación [mas] "antigua" (aproximadamente 400 años antes). Desde las relaciones del período (Babilonio) establecidas en "Sobre las vueltas periódicas de los cinco planetas", él calcula cuantas revoluciones completas en anomalía han ocurrido entre las dos observaciones; y esto mas el incremento en grados derivado desde las dos observaciones da el movimiento total del planeta en anomalía. Se divide esto último por el intervalo en días y en fracciones de día entre las dos observaciones dando el movimiento medio diario en anomalía, y Ptolomeo lo establece explícitamente en cada caso siendo la base del movimiento medio diario utilizado en las Tablas de los Movimientos Medios en Longitud y en Anomalía de los cinco Planetas.
No obstante si uno, realiza los cálculos implicados en los capítulos de arriba utilizando los números de Ptolomeo, en ningún caso uno no encuentra concordancias con los movimientos medios diarios en anomalía que él actualmente lista [3], como se muestra seguidamente.
Los movimientos medios diarios en anomalía de Ptolomeo (Libro IX Capítulo 3) son:
| Planeta | Movimientos Medios Diarios en Anomalía [º/d] | Referencia |
|---|---|---|
| ♄ | 0;57,7,43,41,43,40 | [1] |
| ♃ | 0;54,9,2,46,26,0 | [2] |
| ♂ | 0;27,41,40,19,20,58 | [3] |
| ♀ | 0;36,59,25,53,11,28 | [4] |
| ☿ | 3;6,24,6,59,35,50 | [5] |
| Libro - Capítulo | Planeta | en n Días [d] | recorre m Grados [º] | Grados recorridos por día [º/d] | Referencia |
|---|---|---|---|---|---|
| final del Libro XI Capítulo 7 | ♄ | 36;57,59,45d | 35,11,51;27º | 0;57,7,43,41,44,18º/d [4] | [1a] |
| final del Libro XI Capítulo 3 | ♃ | 38,15,32;57,30d | 34,31,45;45º | 0;54,9,2,45,8,48º/d | [2a] |
| final del Libro X Capítulo 9 | ♂ | 41,38,1;40d | 19,13,1;43º | 0;27,41,40,19,28,7º/d [5] | [3a] |
| final del Libro X Capítulo 4 | ♀ | 41,30,52d | 25,35,38;25º | 0;36,59,25,49,8,51º/d [6] | [4a] |
| final del Libro IX Capítulo 10 | ☿ | 40,50,13;33,45d | 2,6,52,6;53º | 3;6,24,6,58,39,48º/d[7] | [5a] |
La peor de estas discrepancias, aquella la de Júpiter [8], no produce en 400 años un error mayor a un minuto de arco. Por consiguiente esta claro que Ptolomeo aquí no tuvo ningún motivo para "eludir" (y también que es estrictamente ilegítimo derivar un movimiento medio al sexto lugar fraccionario sexagesimal desde las observaciones separadas por solo 400 años). Aunque, también sus observaciones están esencialmente de acuerdo con los movimientos medios diarios que él utiliza, esto último no puede ser derivado desde ellas, al menos no por el método que establece [9].
Una posible alternativa es sugerida por el camino de la derivación de los movimientos medios establecidos en el Libro IX Capítulo 3. Allí Ptolomeo las expresa en la forma de "correcciones" para las relaciones de los períodos, por ej. "para Saturno, 57 vueltas en Anomalía corresponden a 59 años tropicales más 1 ¾ días". Estas son reducidas a grados y días, por ej. "Saturno recorre (en anomalía) 20520º en 21551;18d". Es válido suponer que los recientes [valores] son en realidad primarios, por ej. las correcciones de "más 1 ¾ días", etc. son derivadas de las equivalencias entre días y grados en conjunto con el parámetro de "un año tropical es igual a 365;14,48d" [10]. Estas equivalencias pueden ser derivadas de los pares de observaciones en el Libro IX Capítulo 10, etc., combinadas con las relaciones del período Babilónico, tal como en el siguiente [ejemplo].
Ejemplo: Saturno. Por Hiparco, Ptolomeo conoce que la razón del período Babilónico, de 57 vueltas en anomalía toma lugar en 59 años, por ej. este planeta recorre (57 * 360)º en aproximadamente (59 * 365;14,48)d. Él reconoce desde su par de observaciones, que este recorre 35,11,51;27º en 36,57,59;45d. De la última equivalencia pudo derivar una "corrección" para el período de días en la más antigua [observación], multiplicando 36,57,59;45 por (57 * 360)º y dividiendo el resultado por 35,11,51;27. Esto da 5,59,11;17,59,55...d, ó (redondeado a la sexagésima [parte] más cercana) 21551;18d, como en el Libro IX Capítulo 3. Los cálculos correspondientes para los otros planetas son:
| Planeta | Cálculos | Resultado [d] | Descripción |
|---|---|---|---|
| ♃ | 38,15,32;57,30 * (65 * 360º) / 34,31,45;45 | 7,12,7;36,42,19...d | ó (redondeado) 25927;37d, como en el Libro IX Capítulo 3 |
| ♂ | 41,38,1;40 * (37 * 360º) / 19,13,1;43 | 8,0,57;40,45,50...d | ó (redondeado) 228857;41d . En el texto en el Libro IX Capítulo 3 tiene 28857;53, enmendado por mí a 28857;53 (cf. en este Ejemplo 16 nota de referencia nro. 10 [11]) |
| ♀ | 41,30;52 * (5 * 360º) / 25,35,38;25 | 48,39;40,5,19...d | ó (redondeado) 2919;40d, como en el Libro IX Capítulo 3 [11] |
| ☿ | 40,50,13;33,45 * (145 * 360º) / 2,6,52,6;53 | 4,40,2;24,1...d | ó (redondeado) 16802;24d, como en el Libro IX Capítulo 3 |
De esas "relaciones corregidas del período" los movimientos medios diarios ahora pueden ser derivados:
| Planeta | Cálculos - Resultado [º/d] | Descripción |
|---|---|---|
| ♄ | 20520º en 21551;18d deriva a 0;57,7,43,41,43,39,41...º/d | de acuerdo con [1] |
| ♃ | 23400º en 25927;37d deriva a 0;54,9,2,42,55,52...º/d | en desacuerdo con [2], y peor que en [2a] |
| ♂ | 13320º en 28857;41d deriva a 0;27,41,40,18,39,12...º/d | en desacuerdo con [3], y peor que en [3a] [12] |
| ♀ | 1800º en 2919;40d deriva a 0;36,59,25,53,11,27,36...º/d | de acuerdo con [4] [13] |
| ☿ | 52200º en 16802;24d deriva a 3;6,24,6,59,35,49,55...º/d | de acuerdo con [5] |
Por lo tanto, este procedimiento puede parecer muy adverso, puede ser utilizado para derivar los movimientos medios de Ptolomeo para Saturno, Venus y Mercurio. Sin embargo, falla con mucha pena para Júpiter y Marte, arrojando dudas sobre la validación de esta explicación en general.
Supongamos, en cambio, que Ptolomeo encuentra sus movimientos medios diarios con algún otro método. Entonces, las equivalencias "Saturno recorre 20520º en 21551;18d", etc., pueden ser derivadas directamente por la división de 20520 por 0;57,7,43,41,43,40, etc. [14], y los pares de las observaciones en el Libro IX Capítulo 10, etc.,simplemente están utilizadas como chequeo. Por ej. Ptolomeo encuentra en las observaciones para Saturno un incremento de 351;27º en 364 años 219 ¾ días.
En las Tablas de los Movimientos Medios en Longitud y en Anomalía de los cinco Planetas uno encuentra 351;26,59º para el intervalo recientemente [calculado]. Los números correspondientes para cada uno de los otros planetas son:
| Planeta | Período de Tiempo | Observado [º] | Calculado según las Tablas [º] |
|---|---|---|---|
| ♃ | 377 años 128 días -1 hora | 105;45º | 105;45,48º |
| ♂ | 410 años 231 ⅔ días | 61;43º | 61;42,55º |
| ♀ | 409 años 167 días | 338;25º | 338;27,48º [15] |
| ☿ | 402 años 283 días 13 ½ hora | 246;53º | 246;53,28º |
Por lo tanto, en cada caso, las observaciones pueden ser consideradas justificando los movimientos medios utilizados, dentro de la precisión lograda. Sobre esta asunción, Ptolomeo ha derivado sus movimientos medios desde alguna otra fuente, y simplemente no se molestó en cambiarlas sobre la base de las observaciones que dió (sobre esto fue justificado absolutamente, dado que, como se observó anteriormente, un intervalo de 400 años es suficiente para garantizar mas de 4 lugares de fraccionarios sexagesimales; por supuesto no estuvo justificado en ocultárselo a sus lectores).
Esto todavía deja sin explicar las bases de los actuales movimientos medios. Uno podría conjeturar que ellos fueron derivados desde las observaciones realizadas en un período [de tiempo] más corto (por ej. entre Hiparco y Ptolomeo). Es fácil encontrar, por [medio del] análisis de Diofanto, intervalos de tiempo y de longitud verosímiles que generen números exactos, por ej. para Marte un movimiento en 274 años 189;16 días de 128 revoluciones mas 169;32º derivan a un movimiento medio diario de 0;27,41,40,19,20,57,59º/d. Pero en ausencia de cualquier evidencia de tales observaciones de Hiparco, esto sigue siendo un falso cálculo aritmético, y debemos admitir que el origen de esos números se mantiene [aún] desconocido [16], al menos para Júpiter y Marte, y probablemente para todos los planetas.
| Ir a: Astrónomos en el Almagesto | Contenidos | Ir a: Catálogo de Estrellas de Ptolomeo. Datación en el Almagesto |
Notas de referencia
- ↑ 1,00 1,01 1,02 1,03 1,04 1,05 1,06 1,07 1,08 1,09 1,10 1,11 1,12 1,13 1,14 1,15 1,16 1,17 1,18 1,19 1,20 1,21 1,22 1,23 1,24 1,25 1,26 1,27 1,28 1,29 1,30 1,31 1,32 1,33 1,34

Método de Interpolación por Lagrange. Click en la imagen para ampliar
Fórmula de interpolación solamente entre 2 pares de valores o puntos (X;Y), (i = 0 y 1 en Fórmula Polinómica de Lagrange).
α es el argumento a "entrar" en la columna de las X y el "Valor Interpolado" resulta de la columna de las Y.
Para una interpolación con más de 2 pares de valores (X;Y) verː Método de Interpolación por Lagrange, aunque para los valores que interpola Ptolomeo, con esta fórmula sencilla y reemplazándola con los 4 valores de una tabla, da el mismo resultado que el del astrónomo.
Nota del traductor al español. - ↑ Ptolomeo (l.c.) da 2 ½ horas equinocciales, que es aproximadamente lo mismo.
- ↑ Cf. Newton pp. 320-1, 325-7, donde la discrepancia esta casi correctamente descrita, aunque deriva a consecuencias no válidas.
- ↑ En estos y en subsecuentes cálculos el último lugar esta redondeado sobre la base de un lugar más calculado.
- ↑ Ptolomeo da un incremento de "⅔ día", implicando 6 a.m. para la primera observación y 10 p.m. para la segunda. Si asumimos (de manera improbable) que la segunda fue realizada a las 10;25 p.m. (c.f. en el Libro X Capítulo 7, nota de referencia nro. 3), y el incremento actualmente es de 16;25 horas, esto podría dar un intervalo igual a 41,38,1;41,2,30d, derivando a 0;27,41,40,18,46,32º/d, que incluso [aún] es más discrepante.
- ↑ Sino ver en el Libro X Capítulo 4, nota de referencia nro. 9. El intervalo, que Ptolomeo redondea a días enteros, probablemente debería ser de 1 ¼ o 1 ½ horas menos. Estas correcciones derivan a movimientos diarios de 0;36,59,25,51,56,24º y de 0;36,59,25,52,29,19º, de los cuáles el segundo esta mucho más cerca al, pero aún no idéntico con, el movimiento diario tabulado.
- ↑ Aplicando la ecuación del tiempo de -23 minutos en la observación de Ptolomeo, por ej. tomando el incremento como de 13;7 horas, en cambio de 13 ½, deriva al movimiento diario de 3;6,24,7,3,2º, que incluso es mas discrepante.
- ↑ Asumiendo que corregimos el intervalo para Venus como en la nota de referencia anterior nro. 6.
- ↑ En caso de que alguien conjeturase que Ptolomeo calculó los tiempos de las observaciones más precisamente de lo que él establece (con el ej. en las correcciones para la ecuación del tiempo), noto que en orden de tomar el movimiento medio diario de Tolomeo, exacto al sexto lugar fraccionario sexagesimal, directamente desde las observaciones, estos podrían haber sido registrados con una precisión de segundos, lo que es totalmente increíble.
- ↑ Esto funciona muy bien para todos los planetas excepto para Marte (donde en el texto figura, "28857;53d" siendo ciertamente corrupto: he enmendado "53" en cambio de "43", aunque "42" podría estar en perfecto acuerdo con la hipótesis anterior) y para Mercurio, donde "+1 1/30d" debería ser más bien "+1;3d". Pero, en lugar de enmendar a "1 1/20d" (que es posible), podemos considerar "1 1/30d" simplemente como una pequeña imprecisión.
- ↑ 11,0 11,1 Tomando un intervalo de 1 ¼ o de 1 ½ horas menos (ver más arriba nota de referencia nro. 6) no hay una diferencia al primer lugar fraccionario sexagesimal.
- ↑ Tomando la fracción sexagesimal del día como de 42,43 ó 53 (cf. más arriba con la nota de referencia nro. 10) genera un movimiento medio diario progresivamente más pequeño y [también] progresivamente un mayor desacuerdo.
- ↑ Es interesante que lo aportado se ubica casi exactamente en el medio entre el movimiento medio diario que da Ptolomeo (28 en el último lugar sexagesimal) y aquel por debajo de las secciones para los "años" y los "períodos de 18 años" en las Tablas de los Movimientos Medios en Longitud y en Anomalía de los cinco Planetas (27 en el último lugar sexagesimal, cf. Libro IX Capítulo 3, nota de referencia nro. 12). ¿Es esto un indicio de una revisión incompleta?
- ↑ Aún aquí Marte es un problema, dado que este método también da 28857;41d (cf. más arriba con la nota de referencia nro. 10).
- ↑ Para un intervalo de 1 ½ hora menos (cf. más arriba en la nota de referencia nro. 6) uno encuentra en las tablas 338;25,30º, de acuerdo con el resultado de las observaciones.
- ↑ Una conjetura alternativa es aquella [donde] los movimientos medios incluso fueron derivados de las observaciones dadas, pero aplicando una "corrección" a un movimiento medio anterior (¿la de Hiparco?), por el mismo camino como fue corregido el movimiento medio en la anomalía lunar en el Libro IV Capítulo 7 (y en la latitud lunar en la Inscripción Canóbica). Pero dado que ningún movimiento medio es mencionado por Ptolomeo, los detalles no podrían cambiarse.



