Almagesto: Libro IV - Capítulo 09
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
{Sobre las correcciones de las Posiciones Medias de la Luna, y sus Épocas}
Por medio de los métodos de arriba hemos establecido los movimientos periódicos y las épocas [de la Luna] en longitud y en anomalía. Concernientes a las cantidades correspondientes a su latitud, anteriormente estuvimos equivocados, porque adoptamos también las asunciones de Hiparco de que [el diámetro de] la Luna llega aproximadamente a 650 veces dentro de su propia órbita, y 2 ½ veces dentro [del diámetro de] la Sombra de la Tierra, cuando [la Luna] esta en su distancia media en las Sizigias. Dado que una vez que estas cantidades y el tamaño de la inclinación de la órbita de la Luna son dadas, son dados los límites de los eclipses lunares individuales.
Entonces tomamos [un par de] eclipses separados por un intervalo conocido, (desde la magnitud del oscurecimiento en el eclipse medio) [es] calculada la distancia verdadera [de la Luna] desde cualquiera de los dos nodos [el eclipse estuvo (se ubicó) aproximadamente] a lo largo de su círculo inclinado en el [argumento en] latitud, determinada la posición media [en latitud] desde la verdadera aplicando la Ecuación de la Anomalía como ya se determinó, y así encontrar la Posición Media en Latitud en medio de cada Eclipse, y por lo tanto el movimiento en latitud (como incremento sobre las revoluciones completas) durante este intervalo [2].
Pero ahora, utilizando métodos más elegantes que no requieran alguna de las asunciones previas para la solución del problema, hemos encontrado que es erróneo el movimiento en latitud calculado por el método anterior. Además, el movimiento en latitud calculado con nuestro nuevo método sin aquellas asunciones, hemos probado que muchas de aquellas asunciones concernientes al tamaño y a la distancia son falsas, y [luego] las hemos corregido. Hemos hecho algo similar con la hipótesis para Saturno y Mercurio, cambiando algunas de nuestras primeras asunciones, algunas incorrectas, porque más tarde tuvimos observaciones más precisas.
Ya que aquellos quienes se aproximan a esta ciencia con un verdadero espíritu de investigación y con un amor a la verdad deberían utilizar cualquier nuevo método que descubran, los cuales den resultados más precisos, no para corregir meramente las antiguas teorías, sino también las suyas propias, si ellos lo necesitaran. No deberían pensar en deshonrarse, cuando el objetivo que ellos profesan para seguir es tan grande y divino, incluso [si] sus teorías son corregidas y hechas de [manera] más precisa por otros a la par de ellos mismos. En cuanto a estos temas [sobre las correcciones a las teorías de Saturno y de Mercurio], en la última parte de nuestro tratado explicaremos como tratar con ellas en los lugares apropiados [3]. Por el momento, para preservar el orden propio del procedimiento, volveremos a la demostración de la posición en latitud, que [esta dada] por medio del siguiente método.
Primero, entonces, para corregir el actual movimiento medio en latitud, buscamos [un par de] eclipses lunares (de entre aquellos registrados [en forma] precisa) separados por un intervalo [de tiempo] tan grande como fuera posible, en los que en ambos
- [1] el tamaño del oscurecimiento sea igual
- [2] los eclipses toman lugar cerca del mismo nodo,
- [3] el eclipse ocurrió en el mismo lado (tanto ambos al Norte o ambos al Sur [(de la eclíptica)]) y
- [4] la Luna estuvo cerca de la misma distancia [de la Tierra].
- [1] el tamaño del oscurecimiento sea igual
Si estas condiciones son cumplidas el centro de la Luna debería estar a la misma distancia del mismo nodo, y en el mismo lado, en ambos eclipses, y por lo tanto su movimiento verdadero en latitud durante el intervalo entre las observaciones contiene un número entero de revoluciones en latitud.
El primer eclipse que utilizamos es uno observado en Babilonia en el trigésimo primer año de Darío I, 3/4 de Tybi [V] en el calendario Egipcio, [25/26 de Abril de –490] en la mitad de la sexta hora [de la noche]. Se ha informado que en este eclipse la Luna fue oscurecida 2 dígitos desde el [limbo] Sur [4].
El segundo eclipse que utilizamos es aquel observado en Alejandría en el noveno año de Adriano, 17/18 Pachon [IX] en el calendario Egipcio [5/6 de Abril de 125], 3 ⅗ horas equinocciales antes de la medianoche. En este eclipse también la Luna fue oscurecida ⅙ ta. parte de su diámetro desde el [limbo] Sur [5].
En cada eclipse la posición de la Luna en latitud estuvo cerca del nodo descendente (incluso tales conclusiones pueden ser esbozadas desde hipótesis bastantes imprecisas) [6]. La distancia [de la Luna] fue aproximadamente la misma [en ambos eclipses], y un poco más cerca del perigeo respecto de la distancia media. Esto también puede ser demostrado desde nuestra determinación previa de la anomalía. Ahora, cuando la Luna es eclipsada desde el [limbo] Sur, su centro esta al Norte de la eclíptica. Entonces esta claro que en ambos eclipses el centro de la Luna estuvo a una cantidad igual antes del nodo descendente. En el primer eclipse la distancia de la Luna desde el apogeo del Epiciclo fue de 100;19º. (Dado que la hora del eclipse medio fue ½ hora antes de la medianoche en Babilonia, y [por lo tantos] 1 ⅓ horas equinocciales antes de la medianoche en Alejandría [7]; el tiempo desde la época del 1° año del reinado de Nabonassar viene a ser de
256 años 122 días 10 ⅔ horas recontados simplemente
256 años 122 días 10 ¼ horas recontados en días solares verdaderos.)
Por lo tanto la posición verdadera fue de 5° menos que la media [8]. En el segundo eclipse la Luna estuvo a 251;53° desde el apogeo del epiciclo. (Dado que en este caso el tiempo desde la época del 1° año del reinado [de Nabonassar] hasta la mitad del eclipse llega a ser de
871 años 256 días 8 2/5 horas equinocciales recontados simplemente
871 años 256 días 8 1/12 horas equinocciales recontados en forma precisa.)
Por lo tanto, la posición verdadera fue 4;53º mayor que la [posición] media. En consecuencia, en el intervalo entre los dos eclipses, que comprenden 615 años Egipcios, 133 días y 21 ⅚ horas equinocciales [9], el Movimiento Verdadero en Latitud de la Luna comprende un número entero de revoluciones, mientras su Movimiento Medio llega a poco menos de una revolución completa por 9;53º, que es la suma de ambas [Ecuaciones de la] Anomalía. Pero de acuerdo con los movimientos medios derivados de las hipótesis de Hiparco, como lo establecido anteriormente, en este intervalo llega a poco menos que una revolución completa por alrededor de 10;2º. Por lo tanto el movimiento medio en latitud es mayor de lo que uno podría esperar desde su hipótesis [(la de Hiparco)] por 9 minutos.
Dividimos esos 9 minutos por el total de días en el intervalo anterior (aproximadamente 224609 días), y adicionamos el resultado 0;0,0,0,8,39,18º al Movimiento Medio Diario [en Latitud] derivado anteriormente de aquellas hipótesis, por lo tanto hallamos el movimiento medio corregido [como] de 13;13,45,39,48,56,37º, que nuevamente utilizamos como base para los otros totales acumulados en las tablas.
En este sentido, una vez determinado el movimiento medio en latitud, a continuación procederemos a establecer su posición de la época. Para tal propósito buscamos otro par de eclipses precisamente observados en un intervalo conocido, en el cual todas las mismas condiciones fueron cumplidas como [sucedió] con el par [de eclipses] previos (a saber, para ambos eclipses la distancia de la Luna [a la Tierra] fue aproximadamente igual, y [la magnitud del] oscurecimiento fue igual y ocurrieron en el mismo lado (ambos tanto al Norte o al Sur [de la eclíptica]), excepto que aquí los eclipses estuvieron cerca de los nodos opuestos en cambio de cerca del mismo nodo.
El primero de estos eclipses es aquel que también utilizamos en nuestra demostración de la anomalía (Libro IV Capítulo 6) [10]. Este ocurrió en el segundo año del reinado de Mardokempad, 18/19 de Thoth [I] en el calendario Egipcio [8/9 de Marzo de –719], a medianoche en Babilonia, y a ⅚ de una hora equinoccial antes de la medianoche en Alejandría; en este eclipse esta registrado que la Luna fue oscurecida 3 dígitos desde el [limbo] Sur.
El segundo, que Hiparco también utilizó, ocurrió [11] en el vigésimo año del reinado de Darío quien sucedió a Cambises II, 28/29 de Epiphi [XI] en el calendario Egipcio [19/20 de Noviembre del –501], cuando han pasado de la noche 6 ⅓ de horas equinocciales, nuevamente en este eclipse la Luna fue oscurecida ¼ de su diámetro desde el [limbo] Sur. La mitad del eclipse fue 2/5 de una hora equinoccial antes de la medianoche en Babilonia (dado que la longitud de la mitad de la noche fue de 6 ¾ horas equinocciales en aquella fecha), y [por lo tanto] 1 ¼ de hora equinoccial antes de la medianoche en Alejandría [12].
Ambos de estos eclipses ocurrieron cuando la Luna estuvo cerca de su mayor distancia, aunque el primero estuvo cerca del nodo ascendente, mientras que el segundo estuvo cerca de nodo descendente. Entonces aquí también el centro de la Luna estuvo a una distancia igual al Norte de la Eclíptica en [ambos] eclipses.
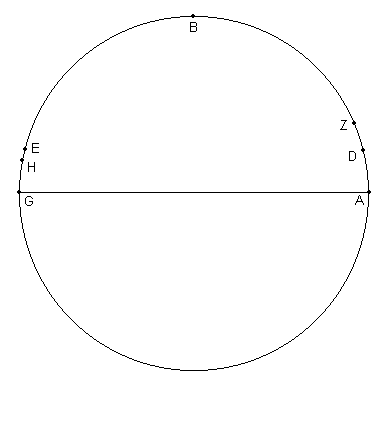
Entonces [ver Fig. 4.11], sea ABG la órbita inclinada de la Luna sobre el diámetro AG. Tomemos el punto A como el nodo ascendente, G como el nodo descendente, y B como el límite Norte. Cortar arcos iguales, AD y GE, desde los nodos A y G hacia el límite Norte B. Luego en el primer eclipse, el centro de la Luna estuvo en D y en el segundo [eclipse] en E.
Ahora el tiempo desde la época desde el 1° año del reinado [de Nabonassar] hasta [la mitad del] primer eclipse es de 27 años Egipcios, 17 días 11 ⅙ horas equinocciales (recontadas ambas simplemente y en forma precisa). Por lo tanto la distancia de la Luna desde el apogeo del epiciclo fue de 12;24º, y la posición media fue mayor que la verdadera por 59º minutos.
Igualmente, el tiempo [desde la época desde el 1° año del reinado de Nabonassar] hasta [la mitad del] segundo eclipse fue de
245 años egipcios, 327 días 10 ¾ horas equinocciales recontados simplemente
245 años egipcios, 327 días 10 ¼ horas equinocciales recontados en forma precisa.
Por lo tanto la distancia de la Luna desde el apogeo del epiciclo fue de 2;44º, y la posición media fue mayor que la verdadera por 13 minutos. El intervalo entre las observaciones contiene 218 años Egipcios, 309 días 23 1/12 horas equinocciales, que producen, para el movimiento medio en latitud deducido arriba, un incremento [sobre revoluciones completas] de 160;4º.
Entonces, debido a lo anterior, sea Z la posición media del centro de la Luna en el primer eclipse [en Fig. 4.11] y en H en el segundo. Entonces, dado que
arco ZBH = 160;4
y arco DZ = 0;59º y arco EH = 0;13º,
arco DE = [arco DZ + arco ZBH – arco EH = ] 160;50º.
En consecuencia (arco AD + arco EG) = 19;10º (suplementario).
Y, ya que ellos son iguales, arco AD = arco EG = 9;35º.
Esta es la cantidad por la cual, en el primer eclipse, la posición verdadera de la Luna estuvo hacia atrás del nodo ascendente, y por la cuál, en el segundo eclipse, la posición verdadera de la Luna estuvo antes del nodo descendente. Por lo tanto, por adición,
arco AZ = [arco AD + arco DZ = ] 10;34º
y, por sustracción
arco HG = [arco EG – arco EH = ] 9;22º.
Por lo tanto la posición media de la Luna en el primer eclipse estuvo 10;34º hacia atrás del nodo ascendente, y [por lo tanto] estuvo a 280;34º desde el límite Norte B, y en el segundo eclipse esta estuvo a 9;22º antes del nodo descendente, y [por lo tanto] su distancia desde el límite Norte [B] fue de 80;38º.
Seguido, ya que el tiempo desde la época [desde el 1° año del reinado de Nabonassar] hasta la mitad del primer eclipse produce un incremento [sobre revoluciones completas] del [movimiento medio en] latitud de 286;19º, sustraemos esta cantidad desde los 280;34º para la posición en el primer eclipse y (después de adicionar 360º) encontrar, para el primer año de Nabonassar, al mediodía del 1 de Thoth en el calendario Egipcio: la posición media en latitud (contada desde el límite Norte [como de]): 354;15º.
Con el fin de permitir chequear los cálculos concernientes a las conjunciones y oposiciones (dado que para aquellas posiciones [de la Luna] no tenemos necesidad [de calcular] la segunda anomalía que demostraremos más tarde), estableceremos una tabla para las [ecuaciones de la anomalía] individuales. La hemos calculado geométricamente, en el mismo sentido como ya lo hicimos para el Sol. En este caso utilizaremos la proporción 60 / 5 ¼ [como base], pero, como [lo hicimos previamente], la tabularemos a intervalos de 6º para los cuadrantes del apogeo, y [con intervalos] de 3º para [los cuadrantes del] perigeo. Por lo tanto el diseño de la tabla es idéntica a aquella del Sol: esta consiste de 45 líneas y 3 columnas; las dos primeras columnas contienen el argumento, en grados de la anomalía, mientras la tercera columna contiene la ecuación correspondiente a cada argumento. Para calcular la longitud y la latitud, esta ecuación tiene que ser sustraída cuando la anomalía, contada desde el apogeo del epiciclo, es [igual] hasta los 180º, y sumada cuando la anomalía es más que 180º. La tabla es la siguiente.
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Libro IV |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 | 11 |
Notas de referencia
- ↑ Ver HAMA 80-2. Pedersen 181 es inadecuado.
- ↑ El método de Hiparco fue inicialmente explicado por Schmidt, “Maanens Middelbevaegelse”. Cf. HAMA 313. Norman T. Hamilton descubrió la relevancia de este pasaje para el valor del movimiento medio de la Luna y de la posición en latitud ambos dados en la Inscripción Canóbica, (Op. Min. 151-2, cf. HAMA 914), y demostró que ellos fueron derivados por la aplicación del método aquí descrito para los dos eclipses del 28° año del reinado de Nabonassar 18/19 de Thoth [I] [8/9 de Marzo –719] (Libro IV Capítulo 6, H303) y del 882° año del reinado de Nabonassar 2/3 de Choiak [IV] [20/21 de Octubre del 134] (Libro IV Capítulo 6, H315). El primero de estos ya había sido utilizado por Hiparco (cf. Libro VI Capítulo 9, H526), quién (por este método) encontró que la Luna estuvo 9º pasado el nodo. Aplicando el movimiento medio en latitud de Hiparco al intervalo entre los eclipses, Ptolomeo encuentra en el segundo eclipse que la Luna debería haber pasado 5º el nodo. Sin embargo, desde la magnitud observada calculó que más bien esta debe estar 6° más allá del nodo, y por lo tanto el movimiento medio “corregido” de Hiparco adicionando 1º, a ser distribuido en los intervinientes 311784 días. Cf. Libro IV Capítulo 7. Esto produce exactamente el valor hallado en la Inscripción Canóbica.
- ↑ No hay nada en las discusiones de Mercurio y de Saturno (Libros IX y XI) que den una guía a los cambios que menciona Ptolomeo, pero el descubrimiento de Hamilton acerca de la teoría lunar en latitud (ver nota de referencia anterior) hace válido lo que Ptolomeo se refiere a diferentes parámetros para Mercurio y Saturno hallados en la Inscripción Canóbica. Estos son: para Saturno, una excentricidad de 3;15p en cambio de 3;25p, el nodo ascendente de 353;30º desde Regulus en cambio de 327;30º; para Mercurio, una excentricidad de 2;30p en cambio de 3-9p [?], la inclinación de la deferente de 0;40º en cambio de 0;45º, la inclinación del epiciclo 7º en cambio de 6;15º, la oblicuidad del epiciclo 2;30º en cambio de 7º (cf. HAMA 908-17).
- ↑ Oppolzer no. 1107: tiempo 19;55 hs. (≈ 22:00 hs. en Alejandría), magnitud 1,1 dígitos. Paul Viktor Neugebauer calcula ca. de 22,7 hs. en Babilonia (≈ 22:15 hs. en Alejandría), 1,7 dígitos.
Fecha y horas calculadas con un programa de computación desde la observación realizada por los Babilonios (actual Bagdad) del siguiente:Eclipse lunar Fecha Tipo Eclipse 1° Contacto con la Umbra Eclipse Medio Último Contacto con la Umbra Duración de la Totalidad Tiempo Total del Eclipse % Oscurecimiento - Magnitud - Dígitos Luna en Carta 25 de Abril de 491 a. C. (-491) Parcial 21:43:11 hs. 22:18:10 hs. 22:53:08 hs. ------ 01:09:56 hs. 3,91 % - 0,0908 - 1,08 dígitos Scorpius 
Almagesto Observación - 25.04.491 a. C. Nota del traductor al español: el cálculo de los dígitos es la fracción sombreada o eclipsada del diámetro lunar siendo igual a la Magnitud actual -menor o igual a 1- multiplicada por 12 dígitos (100% eclipsada). La carta y datos elaborados con mi software de aplicación "M1 Sistema Astronómico"©.
- ↑ Oppolzer no. 2058: tiempo 18;57 hs. (≈ 21:00 hs. en Alejandría), magnitud 2 dígitos. Notar también que este eclipse fue observado en Alejandría, Ptolomeo no dice que él mismo fue el observador. Por conjeturas podemos [decir] que fue observado por Teón de Esmirna quien “transmitió” las observaciones planetarias a Ptolomeo registradas en el Libro IX Capítulo 9 y en el Libro X Capítulos 1 y 2.
Fecha y horas calculadas con un programa de computación desde la observación realizada por Teón de Esmirna (actual Alejandría) del siguiente:Eclipse lunar Fecha Tipo Eclipse 1° Contacto con la Umbra Eclipse Medio Último Contacto con la Umbra Duración de la Totalidad Tiempo Total del Eclipse % Oscurecimiento - Magnitud - Dígitos Luna en Carta 5 de Abril de 125 d. C. (125) Parcial 19:49:02 hs. 20:31:41 hs. 21:14:20 hs. ------ 01:25:17 hs. 7,82 % - 0,1451 - 1,74 dígitos Libra 
Almagesto Observación 05.04.125 d. C. Nota del traductor al español: carta y datos elaborados con mi software de aplicación "M1 Sistema Astronómico"©.
- ↑ Ver HAMA 81 n.4. como ejemplo de como esto pudo haber sido realizado.
- ↑ No es claro si Ptolomeo toma la hora de la observación dada en horas de estación o equinocciales. No obstante, el Sol esta suficientemente cerca del Equinoccio (por ½ hora) siendo mínima la diferencia.
- ↑ El camino más simple de chequear (la cantidad correspondiente en el segundo eclipse) es utilizar la Tabla de la Ecuación [Tabla de la Primer Anomalía Simple de la Luna] (Libro IV Capítulos 10) con los argumentos de 100;19º y 251;53º.
- ↑ Las correcciones de la Ecuación del Tiempo están bastante erróneamente calculadas, siendo cerca de 4 minutos mayor en ambos eclipses. Sin embargo, estas imprecisiones se cancelan en el cálculo del intervalo.
- ↑ Fecha y horas calculadas con un programa de computación desde la observación realizada por los Babilonios (actual Bagdad) del siguiente:
Eclipse lunar Fecha Tipo Eclipse 1° Contacto con la Umbra Eclipse Medio Último Contacto con la Umbra Duración de la Totalidad Tiempo Total del Eclipse % Oscurecimiento - Magnitud - Dígitos Luna en Carta 8-9 de Marzo de 720 a. C. (-720) Parcial 22:44:25 hs. 23:25:08 hs. 00:05:51 hs. ------ 01:21:25 hs. 5,25 % - 0,1111 - 1,33 dígitos Virgo 
Almagesto Observación - 08.03.720 a. C. Nota del traductor al español: carta y datos elaborados con mi software de aplicación "M1 Sistema Astronómico"©.
- ↑ Leer en el manuscrito C y el D en cambio de en H332,14.
Fecha y horas calculadas con un programa de computación desde la observación realizada por los Babilonios (actual Bagdad) del siguiente:Eclipse lunar Fecha Tipo Eclipse 1° Contacto con la Umbra Eclipse Medio Último Contacto con la Umbra Duración de la Totalidad Tiempo Total del Eclipse % Oscurecimiento - Magnitud - Dígitos Luna en Carta 19-20 de Noviembre de 502 a. C. (-502) Parcial 22:42:02 hs. 23:34:27 hs. 00:26:51 hs. ------ 01:44:49 hs. 11,46 % - 0,1889 - 2,26 dígitos Taurus 
Almagesto Observación - 19.11.502 a. C. Nota del traductor al español: carta y datos elaborados con mi software de aplicación "M1 Sistema Astronómico"©.
- ↑ Oppolzer no. 1090: tiempo 21;24 hs. (≈ 23:15 hs. Alejandría), magnitud 2.1 dígitos.
