Almagesto: Libro XI - Capítulo 01
| Ir al Libro X - Capítulo 10 | Contenidos | Capítulo Siguiente |
{Demostración de la Excentricidad y de la (posición del) Apogeo de Júpiter}
Ahora que hemos establecido los movimientos periódicos, las anomalías y las épocas del planeta Marte, seguidamente vamos a tratar con aquellas de Júpiter por el mismo camino. Una vez más, primero tomamos, para demostrar [la posición del] apogeo y [la proporción (razón) de] la excentricidad, tres oposiciones [en las cuáles Júpiter esta] directamente opuesto a la [longitud media del] Sol.
[1] Observamos la primera de esas por medio del instrumento Astrolabio en el decimoséptimo año de Adriano, 1/2 de Epiphi [XI] en el calendario Egipcio [17/18 de Mayo de 133], 1 hora antes de la medianoche, en ♏︎ 23;11º [2];
[2] la segunda en el año vigésimo primero [de Adriano]. 13/14 de Phaophi [II] [31 de Agosto / 1 de Septiembre de 136], 2 horas antes de la medianoche, en ♓︎ 7;54º [3];
[3] y la tercera en el primer año de Antonino Pío, 20/21 de Athyr [III] [7/8 de Octubre de 137], 5 horas después de la medianoche, en ♈︎ 14;23º [4].
Ya que los dos intervalos, aquel desde la primera hasta la segunda oposición comprende:
| [en tiempo] | 3 años Egipcios 106 días 23 horas |
| y en movimiento aparente del planeta | 104;43º |
mientras que [el segundo intervalo] desde la segunda hasta la tercera oposición comprende:
| [en tiempo] | 1 año Egipcio 37 días 7 horas |
| y [en longitud verdadera] | 36;29º |
Por cálculo encontramos que el movimiento medio en longitud
| para el primer intervalo: | 99;55º |
| para el segundo intervalo: | 33;26º |
Desde esos intervalos, siguiendo los métodos expuestos para Marte, llevamos a cabo la demostración que propusimos determinar; primero de todo como si allí hubiera, nuevamente, solo una Excéntrica. La demostración es la siguiente.
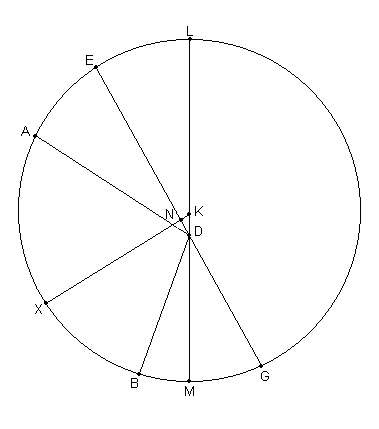
Sea ABG [Fig. 11.1] la excéntrica, sobre la cual el punto A es tomado como la posición central del Epiciclo en la primera oposición, B aquella en la segunda oposición, y G aquella en la tercera. Dentro de la excéntrica ABG tomar D como el centro de la Eclíptica, unir AD, BD y GD, prolongar GD hasta E y dibujar AE, EB y AB, y eliminar las perpendiculares EZ y EH desde E hasta AD y BD, y la perpendicular AΘ desde A hasta EB.
Entonces, dado que el arco BG de la excéntrica esta dado como subtendiendo 36;29º de la eclíptica, el ángulo en el centro de la eclíptica,
el ^ BDG (= ^ EDH) = 36;29º donde 4 ángulos rectos = 360º
el ^ BDG (= ^ EDH) = 72;58ºº donde 2 ángulos rectos = 360ºº.
Por lo tanto, en el circulo alrededor del triángulo rectángulo EDH,
arco EH = 72;58º
y EH = 71;21p donde la hipotenusa DE = 120p.
Similarmente, dado que arco BG = 33;26º,
el ángulo [subtendido por él] en la circunferencia,
el ^ BEG = 33;26ºº donde 2 ángulos rectos = 360ºº;
y, por sustracción [del ^ BEG desde ^ EDH],
el ^ EBH = 39;32ºº en las mismas unidades.
Por lo tanto, en el círculo alrededor del triángulo rectángulo BEH,
arco EH = 39;32º
y EH = 40;35p donde la hipotenusa BE = 120p.
Por lo tanto donde EH, como demostramos, es de 71;21p, y ED = 120p,
BE = 210;58p.
Además, dado que el todo el arco ABG de la excéntrica esta dado subtendiendo 141;12º de la eclíptica (la suma de ambos intervalos [104;43° y 36;29°]), el ángulo en el centro de la eclíptica,
el ^ ADG = 141;12º donde 4 ángulos rectos = 360º
el ^ ADG = 282;24ºº donde 2 ángulos rectos = 360ºº,
y su [ángulo] complementario, el ^ ADE = 77;36ºº en las mismas unidades.
Por lo tanto, en el círculo alrededor del triángulo rectángulo DEZ,
arco EZ = 77;36º
y EZ = 75;12p donde la hipotenusa DE = 120p.
Similarmente, dado que el arco ABG de la excéntrica es, por adición [de 99;55º + 33;26º], 133;21º, el ángulo [subtendido por él] en la circunferencia,
el ^ AEG = 133;21ºº donde 2 ángulos rectos = 360ºº.
Pero el ^ ADE fue encontrado ser de 77;36ºº en las mismas unidades.
Por lo tanto el ángulo restante [en el triángulo EAD],
el ^ EAZ = 149;3ºº en las mismas unidades.
Por lo tanto, en el círculo alrededor del triángulo rectángulo AEZ,
arco EZ = 149;3º
y EZ = 115;39p donde la hipotenusa EA es de 120p.
Por consiguiente donde EZ, como fue demostrado, es de 75;12p, y ED esta dado como de 120p,
EA = 78;2p.
Además, dado que el arco AB de la excéntrica es de 99;55º, el ángulo [subtendido por él] en la circunferencia,
el ^ AEB = 99;55ºº donde 2 ángulos rectos = 360ºº.
Por lo tanto, en el círculo alrededor del triángulo rectángulo AEΘ,
arco AΘ = 99;55º
y arco EΘ = 80;5º (suplementario).
Por lo tanto las cuerdas correspondientes
AΘ = 91;52p donde la hipotenusa EA = 120p.
Y EΘ = 77;12p donde la hipotenusa EA = 120p.
Por lo tanto donde AE, como fue demostrado, es de 78;2p, y DE = 120p,
AΘ = 59;44p
y EΘ = 50;12p.
Pero toda la línea EB fue demostrada ser de 210;58p en las mismas unidades.
Entonces, por sustracción, ΘB = 160;46p donde AΘ = 59;44p.
Y arco ΘB² = 25845;55
ΘA² = 3568;4,
entonces ΘB² + ΘA² = AB² = 29413;59.
En consecuencia AB = 171;30p donde ED es de 120p y EA es de 78;2p.
Además, donde el diámetro de la excéntrica es de 120p,
AB = 91;52p (dado que este subtiende un arco de 99;55º).
Por lo tanto donde AB = 91;52p y el diámetro de la excéntrica es de 120p,
ED= 64;17p
y EA = 41;47p.
Por lo tanto el arco EA de la excéntrica es igual a 40;45º,
y el arco total EABG [= 40;45º + 133;21º] = 174;6º.
Por lo tanto EDG ≈ 119;50p donde el diámetro de la excéntrica es de 120p.
Por ende, el segmento EABG es menor que un semicírculo, entonces el centro de la excéntrica se ubicará fuera de él. Sea este, entonces, [esta ubicado] en K [ver Fig. 11.2], y dibujar a través de K y de D el diámetro LKDM a través de ambos centros, y sea la perpendicular desde K hasta GE sea prolongada como KNX.
Entonces, donde el diámetro LM = 120p,
toda la línea EG fue demostrada ser de 119;50p, y ED ser de 64;17p;
entonces por sustracción, GD = 55;33p en las mismas unidades.
Entonces, dado que ED * DG = LD * DM,
LD * DM = 3570;56p donde el diámetro LM = 120p.
Pero LD * DM + DK² = LK² (por ej. el cuadrado sobre la mitad del diámetro).
Por lo tanto, si sustraemos (LD * DM), por ej. 3570;56, desde el cuadrado sobre la mitad del diámetro, por ej. 3600, el resto será el cuadrado sobre DK,
por ej. DK² = 29;4.
Por lo tanto la distancia entre los centros, DK ≈ 5;23p [5]
donde el radio de la excéntrica, KL = 60p.
Además, dado que
GN = ½ * GE = 59;55p donde el diámetro LM = 120p,
y GD fue demostrado ser de 55;33p en las mismas unidades,
por sustracción, DN = 4;22p donde DK = 5;23p.
Por lo tanto donde la hipotenusa [del triángulo rectángulo DKN] DK = 120p,
DN = 97;20p,
y, en el círculo en el triángulo rectángulo DKN,
arco DN = 108;24º.
En consecuencia el ^ DKN 108;24ºº donde 2 ángulos rectos = 360ºº
En consecuencia el ^ DKN 54;12º donde 4 ángulos rectos = 360º.
Y dado que DKN es un ángulo en el centro de la excéntrica,
también el arco MX = 54;12º.
Pero el arco total GMX, que es ½ arco de GXE, es igual a 87;3º.
Por lo tanto, por sustracción, el arco desde el perigeo hasta la tercera oposición,
arco MG = 32;51º [6].
Y claramente, dado que el intervalo BG esta dado como de 33;26º, por sustracción, encontramos el arco desde la segunda oposición hasta el perigeo,
arco BM = 0;35º [7];
y dado que el intervalo AB es dado como de 99;55º, por sustracción [del (arco AB + arco BM) desde los 180º], encontramos el arco desde el apogeo hasta la primera oposición,
arco LA = 79;30º.
Ahora, si este fuera esta excéntrica sobre la cual el centro del epiciclo es transportado, las cantidades anteriores podrían ser lo suficientemente precisas para utilizarlas. Sin embargo, ya que, de acuerdo a nuestra hipótesis, [el centro del epiciclo] se mueve sobre un círculo diferente, a saber el círculo descrito con centro en el punto bisecando [dividiendo en dos o en dos partes iguales a] DK y con el radio KL, debemos una vez más, como lo hicimos para Marte, calcular primero las diferencias que resultan en los intervalos aparentes [por ej. los arcos de la eclíptica entre las oposiciones]: debemos demostrar que los tamaños de esas diferencias podrían ser (tomando la proporción anterior para la excentricidad aproximadamente como la correcta), si el centro del epiciclo fuera transportado, no sobre la segunda excéntrica, sino sobre la primera excéntrica [por ej. la Ecuante], la cual produce la anomalía eclíptica, por ej. la dibujada en el centro K.
Entonces [ver Fig. 11.3] sea LM la excéntrica con centro en D transportando el centro del epiciclo, y NX la excéntrica del movimiento medio del planeta con centro en Z, igual a LM. Dibujar el diámetro a través de los centros, NLM, y tomar sobre él a E, el centro de la eclíptica. Sea el centro del epiciclo situado, primero, en A, para la primera oposición. Dibujar DA, EA, ZAX y EX, y eliminar las perpendiculares DH y EΘ desde D y E hasta AZ prolongada.
Entonces, ya que el ángulo del movimiento medio en longitud, ^ NZX, fue demostrado ser de 79;30º donde 4 ángulos rectos = 360º, el ángulo verticalmente opuesto a él,
el ^ DZH = 79;30º donde 4 ángulos rectos = 360º
el ^ DZH = 159ºº donde 2 ángulos rectos = 360ºº.
Por lo tanto, en el círculo alrededor del triángulo rectángulo DZH,
arco DH = 159º
y arco ZH = 21º (suplementario).
Por lo tanto las cuerdas correspondientes
DH = 117;59p donde la hipotenusa DZ = 120p
y ZH = 21;52p donde la hipotenusa DZ = 120p.
Por lo tanto donde DZ (= ½ * EZ) ≈ 2;42p y el radio de la excéntrica, DA = 60p,
DH = 2;39p
y ZH = 0;30p.
Y dado que DA² - DH² = AH²
AH = 59;56p en las mismas unidades.
Similarmente, dado que ZH = HΘ, EΘ = 2 * DH,
por adición, AΘ = 60;26p donde EΘ = 5;18p,
y por lo tanto la hipotenusa [del triángulo rectángulo AEΘ]
AE = 60;40p en las mismas unidades.
Por lo tanto, donde AE = 120p, EΘ = 10;29p,
Y, en el círculo alrededor del triángulo rectángulo AEΘ,
arco EΘ ≈ 10;1º.
En consecuencia el ^ EAΘ = 10;1ºº donde 2 ángulos rectos = 360ºº.
Además, donde EΘ = 5;18p,
(por lo tanto, obviamente, por suma, XΘ = 61p).
Entonces encontramos la hipotenusa EX [del triángulo rectángulo EΘX] como de 61;14p en las mismas unidades.
y, en el círculo alrededor del triángulo rectángulo EΘX,
arco EΘ = 9;55º.
En consecuencia el ^ EXΘ = 9;55ºº donde 2 ángulos rectos = 360ºº.
Pero demostramos que el ^ EAΘ = 10;1ºº en las mismas unidades.
Por lo tanto, por sustracción, el ángulo de la diferencia en cuestión,
el ^ AEX = 0;6ºº donde 2 ángulos rectos = 360ºº
el ^ AEX = 0;3º donde 4 ángulos rectos = 360º.
Pero en la oposición del planeta, visto a lo largo de la línea EA, [este] tuvo una longitud aparente de ♏︎ 23;11º. Por lo tanto esta claro que, si el centro del epiciclo fuese transportado, no sobre la excéntrica LM, sino sobre [la excéntrica] NX, podría haber estado en el punto X sobre esta excéntrica, y el planeta podría haber aparecido a lo largo de la línea EX, difiriendo por 0;3º [desde la posición actual], y en consecuencia podría haber tenido una longitud de ♏︎ 23;14º.
Sea el diagrama dibujado para la segunda oposición, nuevamente, con una figura similar [ a la Fig. 11.4] [8], [con el centro del epiciclo] descrito como un poco hacia adelante del perigeo.
Entonces, dado que el arco XN de la Excéntrica fue demostrado [arriba en Fig. 11.2, arco BM] ser de 0;35º,
el ^ XZN = 0;35º donde 4 ángulos rectos = 360º
el ^ XZN = 1;10ºº donde 2 ángulos rectos = 360ºº.
Por lo tanto, en el círculo alrededor del triángulo rectángulo DZH,
arco DH = 1;10º
y arco ZH = 178;50º (suplementario).
Por lo tanto las cuerdas correspondientes
DH = 1;13p donde la hipotenusa DZ = 120p
y ZH ≈ 120p donde la hipotenusa DZ = 120p.
Por lo tanto donde DZ = 2;42p y el radio de la excéntrica, DB = 60p,
DH = 0;2p
y ZH = 2;42p.
Y HB = 60p en las mismas unidades (dado que esta es insignificantemente más pequeña que la hipotenusa BD [del triángulo rectángulo HBD]).
Además, dado que ΘH = HZ, y EΘ = 2 * DH,
por sustracción, ΘB = 57;18p donde EΘ = 0;4p.
Por lo tanto la hipotenusa [del triángulo rectángulo EΘB] EB = 57;18p en las mismas unidades.
Por lo tanto, donde EB = 120p, EΘ ≈ 0;8p,
y, en el círculo alrededor del triángulo rectángulo BEΘ,
también el arco EΘ = 0;8º.
En consecuencia el ^ EBΘ = 0;8ºº donde 2 ángulos rectos = 360ºº.
Por el mismo camino, dado que demostramos que toda la línea ZΘ [= 2 * ZH] = 5;24p donde el radio de la excéntrica, ZX = 60p,
por sustracción, ΘX = 54;36p donde EΘ = 0;4p.
Por lo tanto la hipotenusa [del triángulo rectángulo EΘX] EX = 54;36p en las misas unidades.
Por lo tanto, donde EX = 120p, EΘ ≈ 0;10p,
y, en el círculo alrededor del triángulo rectángulo EΘX,
arco EΘ = 0;10°
en consecuencia el ^ EXΘ = 0;10ºº donde 2 ángulos rectos = 360ºº,
y, por sustracción [del ^ EBΘ], el ^ BEX = 0;2ºº en las mismas unidades
y, por sustracción [del ^ EBΘ], el ^ BEX = 0;1º donde 4 ángulos rectos = 360º.
Aquí, entonces, esta claro que el planeta, desde su longitud aparente en la segunda oposición, cuando esta fue observada a lo largo de la línea EB, estuvo en ♓︎ 7;54º, podría, si este ha sido visto a lo largo de la línea EX, haber tenido una longitud de solo ♓︎ 7;53º.
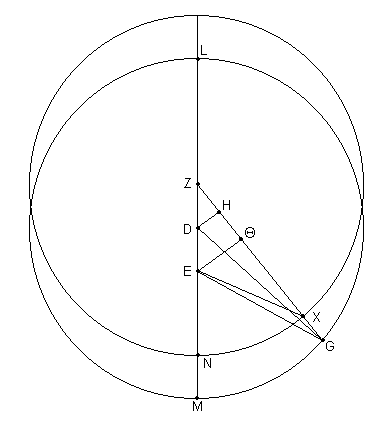
Entonces sea dibujado el diagrama para la tercera oposición, hacia atrás del perigeo [Fig. 11.5] [9].
Entonces, dado que el arco NX de la excéntrica esta dado como de 32;51º,
el ^ NZX = 32;51º donde 4 ángulos rectos = 360º
el ^ NZX = 65;42ºº donde 2 ángulos rectos = 360ºº.
Por lo tanto, en el círculo alrededor del triángulo rectángulo DZH,
arco DH = 65;42º
y arco ZH = 114;18º (suplementario).
Por lo tanto las cuerdas correspondientes
DH = 65;6p donde la hipotenusa DZ = 120p
y ZH = 100;49p donde la hipotenusa DZ = 120p.
Por lo tanto donde DZ = 2;42p y el radio de la excéntrica, DG = 60p,
DH = 1;28p
y ZH = 2;16p.
Y dado que GD² - DH² = GH²,
GH ≈ 59;59p.
Similarmente, dado que ΘH = HZ, y EΘ = 2 * DH,
por sustracción, GΘ = 57;43p donde EΘ = 2;56p.
Por lo tanto, la hipotenusa [del triángulo rectángulo EΘG] EG = 57;47p en las mismas unidades.
Por lo tanto, donde EG = 120p, EΘ = 6;5p,
y, en el círculo alrededor del triángulo rectángulo GEΘ,
arco EΘ ≈ 5;48º.
En consecuencia el ^ EGΘ = 5;48ºº donde 2 ángulos rectos = 360ºº.
Por el mismo camino, dado que toda la línea ZΘ [= 2 * ZH] viene a ser de 4;32p
donde el radio de la excéntrica, ZX = 60p,
por sustracción, XΘ = 55;28p donde EΘ fue encontrada ser de 2;56p.
Por lo tanto la hipotenusa [del triángulo rectángulo EΘX] EX = 55;33p en las mismas unidades.
Por lo tanto, donde EX = 120p, EΘ = 6;20p,
Y, en el círculo alrededor del triángulo rectángulo EΘX,
arco EΘ = 6;2º.
En consecuencia ^ EXΘ = 6;2ºº donde 2 ángulos rectos = 360ºº,
y, por sustracción [del ^ EGΘ], el ^ GEX = 0;14ºº en las mismas unidades
y, por sustracción [del ^ EGΘ], el ^ GEX = 0;7º donde 4 ángulos rectos = 360º.
Por lo tanto, dado que el planeta en la 3 era. oposición, cuando fue observado a lo largo de la línea EG, tuvo una longitud de ♈︎ 14;23º, esta claro que, si este ha estado sobre la línea EX, podría haber tenido una longitud de ♈︎ 14;30º. Y demostramos que sus longitudes [corregidas] [podrían haber sido]
| en la primera oposición ♏︎ | 23;14º |
| en la segunda oposición ♓︎ | 7;53º |
Por consiguiente calculamos los intervalos aparentes [en longitud] del plantea, tomados, no con respecto a la excéntrica transportando el centro del epiciclo, sino con respecto a la excéntrica produciendo el movimiento medio [ej. de la ecuante] [10], como de
| desde la primera hasta la segunda oposición | 104;39º |
| desde la segunda hasta la tercera oposición | 36;37º |
Comenzando con estos datos, por medio del teorema previamente demostrado encontramos la distancia entre los centros de la eclíptica y de la excéntrica produciendo el movimiento medio del epiciclo como alrededor de
5;30p donde le diámetro de la excéntrica es de 120p;
y, para los arcos de la excéntrica,
| desde el apogeo hasta la primera oposición: | 77;15º |
| desde la segunda oposición hasta el perigeo | 2;50º |
| desde el perigeo hasta la tercera oposición | 30;36º |
Las cantidades anteriores han sido determinadas precisamente por este método, dado que las diferencias en los intervalos (medidos a lo largo de la Deferente y de la Ecuante), cuando son calculados con estos datos, son cercanamente las mismos como en el conjunto previo [11]. [También] esta claro el hecho que los intervalos aparentes [en longitud] del planeta derivados desde las proporciones que por lo tanto hemos encontrado llegar a ser los mismos que los observados; podemos demostrar esto del siguiente modo.
Una vez más, sea dibujado el diagrama para la primera oposición [Fig. 11.6], pero conteniendo solamente la excéntrica transportando el centro del epiciclo. Entonces, dado que el ^ LZA fue demostrado ser de 77;15º donde 4 ángulos rectos = 360º, el ^ LZA = ^ DZH (opuesto verticalmente) = 154;30ºº donde 2 ángulos rectos = 360ºº.
Por lo tanto, en el círculo alrededor del triángulo DZH,
arco DH = 154;30º
y arco ZH = 25;30º (suplementario).
Por lo tanto las cuerdas correspondientes
DH = 117;2p donde la hipotenusa DZ = 120p
y ZH = 26;29p donde la hipotenusa DZ = 120p.
Por lo tanto donde ZD = 2;45p y el radio de la excéntrica DA = 60p,
DH = 2;41p
y ZH = 0;36p.
Entonces, por el mismo argumento, como en la previa prueba,
y, por adición [de HΘ = ZH], AΘ = 60;32p donde EΘ (= 2 * DH) = 5;22p.
Por lo tanto la hipotenusa [del triángulo rectángulo AEΘ] AE viene a ser de 60;46p en las mismas unidades.
y, en el círculo alrededor del triángulo rectángulo AEΘ,
arco EΘ = 10;8º.
En consecuencia el ^ EAΘ = 10;8ºº donde 2 ángulos rectos = 360ºº,
y, por sustracción [del ^ EAΘ desde ^ LZA],
el ^ LEA = 144,22ºº en las mismas unidades
el ^ LEA = 72;11º donde 4 ángulos rectos = 360º.
Aquellos [72;11º], entonces, fue la distancia en la eclíptica [12] del planeta desde su apogeo en la primera oposición.
Nuevamente, sea dibujado el diagrama [correspondiente] para la segunda oposición [Fig. 11.7]. [Luego,] dado que
el ^ BZM es dado como 2;50º donde 4 ángulos rectos = 360º
el ^ BZM es dado como 5;40ºº donde 2 ángulos rectos = 360ºº,
en el círculo alrededor del triángulo rectángulo DZH,
arco DH = 5;40º
y arco ZH = 174;20º (suplementario).
Por lo tanto las cuerdas correspondientes
DH = 5;55p donde la hipotenusa DZ = 120p
y ZH = 119;51p donde la hipotenusa DZ = 120p.
Por lo tanto donde DZ = 2;45p y el radio de la excéntrica, DB = 60p,
DH = 0;8p
y ZH ≈ 2;45p.
Y, por el mismo [argumento como el previo],
BH ≈ 60p en las mismas unidades,
y, por sustracción [de HΘ = ZH], BΘ = 57;15p donde EΘ = 0;16p.
Por consiguiente la hipotenusa [del triángulo rectángulo EBΘ] EB viene a ser de 57;15p en las mismas unidades.
Por lo tanto, donde EB = 120p, EΘ = 0;33p,
y, en el círculo alrededor del triángulo rectángulo BEΘ,
arco EΘ = 0;32º.
En consecuencia el ^ EBΘ = 0;32ºº donde 2 ángulos rectos = 360ºº.
Y, por adición [del ^ BZM], ^ BEM = 6;12ºº en las mismas unidades
Y, por adición [del ^ BZM], ^ BEM = 3;6º donde 4 ángulos rectos = 360ºº.
Por lo tanto la distancia del planeta hacia adelante del perigeo en la segunda oposición fue de 3;6º. Y demostramos [Fig. 11.6] que en la primera oposición este estuvo a 72;11º hacia atrás del apogeo [13]. Por lo tanto el intervalo aparente calculado desde la primera hasta la segunda oposición es el suplemento [de 3;6º + 72;11º], 104;43º, de acuerdo con el intervalo derivado desde las observaciones [descritas al principio de este capítulo].
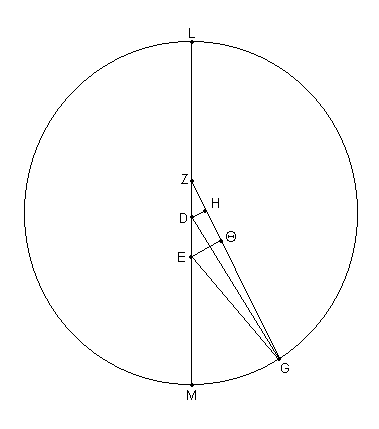
Entonces sea dibujado [Fig. 11.8] el diagrama [correspondiente] para la tercera oposición. [Entonces,] dado que
el ^ MZG fue mostrado ser 30;36º donde 4 ángulos rectos = 360º
el ^ MZG fue mostrado ser 61;12º donde 2 ángulos rectos = 360ºº,
en el círculo alrededor del triángulo rectángulo DZH,
arco DH = 61;12º
y arco ZH = 118;42º (suplementario).
Por lo tanto las cuerdas correspondientes
DH = 61;6p donde la hipotenusa DZ = 120p
y ZH = 103;17p donde la hipotenusa DZ = 120p.
Por lo tanto donde DZ = 2;45p y el radio de la excéntrica, GD = 60p,
DH = 1;24p
y ZH = 2;22p.
Y, por el mismo [argumento como el previo],
GH = 59;59p,
y, por sustracción [de HΘ = ZH], GΘ = 57;37p donde EΘ = 2;48p.
Por lo tanto la hipotenusa [del triángulo rectángulo EGΘ] EG = 57;41p en las mismas unidades;
y por consiguiente, donde EG = 120p, EΘ = 5;50p,
y, en el círculo alrededor del triángulo rectángulo GEΘ,
arco EΘ = 5;34º
en consecuencia ^ EGΘ = 5;34ºº donde 2 ángulos rectos = 360ºº.
Y, por suma [del ^ MZG],
el ^ MEG = 66;46ºº en las mismas unidades
el ^ MEG = 33;23º donde 4 ángulos rectos = 360º.
Estos [33;23º], entonces, fue la distancia del planeta hacia atrás desde el perigeo en la tercera oposición. Y demostramos que en la segunda oposición su distancia hacia adelante del mismo perigeo fue de 3;6º. Por lo tanto el intervalo [en longitud] aparente desde la segunda hasta la tercera oposición es calculado como la suma [anterior de], 36;29º, una vez más de acuerdo con el intervalo observado [al principio de este capítulo].
Inmediatamente esta claro, dado que el planeta en la tercera oposición tuvo una longitud observada de ♈︎ 14;23º y, como fue demostrado, estuvo 33;23º hacia atrás del perigeo, esto [ocurrió] en ese momento [en el que] el perigeo de su excéntrica tuvo una longitud de ♓︎ 11º, mientras su apogeo estuvo diametralmente opuesto en ♍︎ 11º.
Y si dibujamos el epiciclo HΘK alrededor del centro G [ver Fig. 11.9] [14], inmediatamente tendremos:
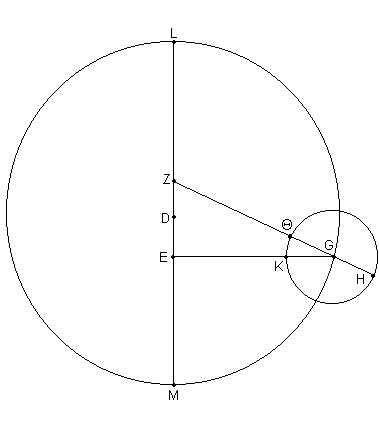
L, la posición en longitud media [contada] desde el apogeo de la excéntrica, como de 210;36º (dado que hemos demostrado que el ^ MZG = 30;36º); y el arco ΘK del epiciclo desde el perigeo Θ hasta K, [la posición del] planeta, como de 2;47º (ya que demostramos que
el ^ EGZ = 5;34ºº donde 2 ángulos rectos = 360ºº
el ^ EGZ = 2;47º donde 4 ángulos rectos = 360º).
Por lo tanto en aquel momento de la tercera oposición, a saber en el primer año de Antonino Pío, 20/21 de Athyr [III] en el calendario Egipcio, 5 horas después de la medianoche, el planeta Júpiter tuvo las siguientes posiciones medias [4]:
| en longitud, desde el apogeo de la excéntrica (por ej. su longitud media estuvo en ♈︎ 11;36º) | 210;36º |
| en anomalía, desde H el apogeo del epiciclo | 182;47º |
| Ir al Libro X - Capítulo 10 | Contenidos | Capítulo Siguiente |
| Libro XI |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 | 11 | 12 |
Notas de referencia
- ↑ El procedimiento para Júpiter y Saturno es idéntico como aquel para Marte (excepto que pocas iteraciones son requeridas). Al lector se remiten las notas en el Libro X Capítulos: 7, 8 y 9 para dilucidar los puntos de detalle.
- ↑
Fecha y horas calculadas con un programa de computación desde la observación realizada por Ptolomeo (actual Alejandría) de la siguiente:
Oposición de Júpiter en el día de la observación de Ptolomeo Fecha Hora Longitud del Sol Longitud de Júpiter Latitud de Júpiter Elongación Altura Azimut Magnitud Júpiter en Carta 17 de Mayo de 133 d. C. (133) 23:00 hs. ♉︎ 54° 49' 52,83" ♏︎ 234° 08' 26" +00° 47' 57,34" E 178° 58' 11" 39° 05' 55" 344° 22' 24" -2,6 Ophiuchus 
Almagesto Observación 17.05.133 d. C. En ese instante, Júpiter se encontraba a: 1° 28' 15" (SW) de Xi Ophiuchus.
La oposición de Júpiter ocurrió el 17 de Mayo de 133 d. C. (133) a las 07:35:37 hora local. Ese mismo día pasaba por el meridiano del lugar a las 23:50:42 hs., altura: 40° 34' y azimut: 0°. Distancia Tierra-Júpiter: 637.286.926,20 kms.
Nota del traductor al español: carta y datos elaborados con mi software de aplicación "M1 Sistema Astronómico"©.
- ↑
Fecha y horas calculadas con un programa de computación desde la observación realizada por Ptolomeo (actual Alejandría) de la siguiente:
Oposición de Júpiter en el día de la observación de Ptolomeo Fecha Hora Longitud del Sol Longitud de Júpiter Latitud de Júpiter Elongación Altura Azimut Magnitud Júpiter en Carta 31 de Agosto de 136 d. C. (136) 22:00 hs. ♍︎ 156° 58' 45" ♓︎ 338° 59' 28" -01° 43' 04" W 177° 21' 27" 38° 32' 42" 317° 33' 10" -2,9 Pisces 
Almagesto Observación 31.08.136 d. C. En ese instante, Júpiter se encontraba a: 8° 31' 57" (SE) de Omega Pisces y a 9° 15' 20" (N) de Iota Cetus (Deneb Al-Shemali).
La oposición de Júpiter ocurrió el 2 de Septiembre de 136 d. C. (136) a las 17:19:34 hora local. Ese mismo día pasaba por el meridiano del lugar a las 00:04:39 hs., altura: 48° 52' y azimut: 0°. Distancia Tierra-Júpiter: 593.903.543,90 kms.
Nota del traductor al español: carta y datos elaborados con mi software de aplicación "M1 Sistema Astronómico"©.
- ↑ 4,0 4,1
Fecha y horas calculadas con un programa de computación desde la observación realizada por Ptolomeo (actual Alejandría) de la siguiente:
Oposición de Júpiter en el día de la observación de Ptolomeo Fecha Hora Longitud del Sol Longitud de Júpiter Latitud de Júpiter Elongación Altura Azimut Magnitud Júpiter en Carta 8 de Octubre de 137 d. C. (137) 05:00 hs. ♎︎ 193° 49' 47" ♈︎ 15° 25' 03" -01° 36' 33" W 177° 43' 56" 14° 45' 18" 86° 30' 25" -2,9 Aries 
Almagesto Observación 08.10.137 d. C. En ese instante, Júpiter se encontraba a: 2° 12' 36" (SW) de Omicrón Aries.
La oposición de Júpiter ocurrió el 9 de Octubre de 137 d. C. (137) a las 14:36:53 hora local. Ese mismo día pasaba por el meridiano del lugar a las 23:49:34 hs., altura: 63° 21' y azimut: 0°. Distancia Tierra-Júpiter: 599.887.458,70 kms.
Nota del traductor al español: carta y datos elaborados con mi software de aplicación "M1 Sistema Astronómico"©.
- ↑ Debido a una acumulación de errores de redondeo este debería ser de 5;20p.
- ↑ La acumulación de errores por redondeo de Ptolomeo ha llegado a una considerable discrepancia de ½º respecto del resultado exacto de 32;21º.
- ↑ Las pequeñeces en las correcciones para esta y la siguiente oposición demuestran que tales oposiciones han sido muy mal elegidas. Para visualizar la máxima diferencia entre los modelos de la excéntrica simple y de la Ecuante, todas las tres oposiciones deberían estar cerca de los octantes [(45°)] (como lo están para Marte).
- ↑ La figura de Heiberg (pág. 371) esta equivocada: ha sido unida en cambio de , y es un error de impresión siendo [el válido]. Corregida por Manitius.
- ↑ La figura de Heiberg (pág. 373) esta equivocada: ha sido unida en cambio de , y esta en el lugar equivocado y es un error de impresión siendo [el válido]. Corregida por Manitius.
- ↑ Por ej. los intervalos aparentes que podrían resultar si el epiciclo fuera transportado, no sobre la actual Deferente, sino sobre la Ecuante. Cf. Libro XI Capítulo 5 antes de la Fig. 11.14, donde es establecido explícitamente. Cf. ver también Libro X Capítulo 7 Fig. 10.12.
- ↑ Incluso, una iteración posterior produce un cambio mucho menor que 0;1p en la excentricidad, y alrededor de 0;10º en la línea de los Ápsides.
- ↑ Por lo que debemos traducir (por ej. tomarla aproximadamente como ) en H377,16, para darle algún sentido sobre todo. Pero su posición en la sentencia, y redundancia, me hace suponer que es una interpolación, aunque lo esta en todas las ramas en la tradición de los manuscritos.
- ↑ Leer (en los manuscritos D y Ar), en cambio de ("hacia atrás"). Corregido por Manitius.
- ↑ La figura de Heiberg en la pág. 381 es incorrecta: ha unido en cambio de . Corregido por Manitius.
