Almagesto: Libro VIII - Capítulo 05
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
{Sobre las Salidas, Culminaciones y Puestas simultáneas de las Estrellas Fijas}
Dadas las definiciones anteriores, los tiempos de las Salidas, de las Culminaciones y de las Puestas simultáneas verdaderas, que son observados con respecto al centro del Sol, pueden ser hallados inmediatamente por nosotros por métodos puramente geométricos desde la posición de [las estrellas en cuestión] en la delineación de las estrellas ([que observamos] sobre el Globo Sólido). Dado que los puntos sobre la Eclíptica con los que cada estrella fija simultáneamente Culmina, Sale o se Pone pueden ser derivados geométricamente por medio de los teoremas [ya] establecidos [2].
Primero, para demostrar las "culminaciones simultáneas", sea ABGD [Fig. 8.1.] [3] el círculo a través de los polos, aquel del Ecuador y aquel de la Eclíptica. Sea AEG un semicírculo del Ecuador alrededor del polo Z, y BED un semicírculo de la Eclíptica alrededor del polo H. Dibujar el segmento HΘKL del gran círculo a través de los polos de la Eclíptica, y tomar sobre él el punto Θ como la estrella fija requerida (dado que ésta esta con respecto a dichos círculos [por ej. los grandes círculos a través de los polos de la Eclíptica, sobre] los cuales hemos observado y registrado las posiciones de las estrellas fijas). También, dibujar el segmento del gran círculo ZΘMN a través de los polos del Ecuador y de la estrella en Θ.
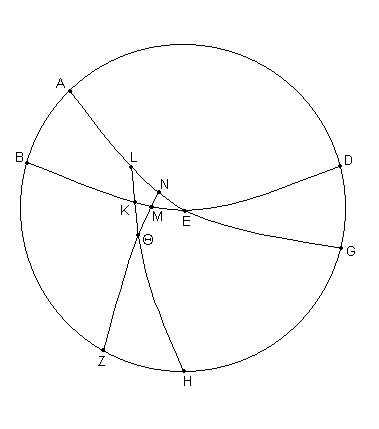
Ahora, es obvio que la estrella [ubicada] en Θ culmina simultáneamente con los puntos M y N de la Eclíptica y del Ecuador [respectivamente]. Pero estos puntos, y el arco ΘN, están dados, como tan claro lo será desde las siguientes consideraciones. De lo que hemos podido comprobar al principio de nuestro tratado (Libro I Capítulo 13), ya que los [dos] arcos HL y NZ del gran círculo han sido dibujados para encontrarse [con] los dos arcos AH y AN del gran círculo,
| Cuerda arco 2 * HA / Cuerda arco 2 * AZ = (Cuerda arco 2 * HL / Cuerda arco 2 * LΘ) * (Cuerda arco 2 * NΘ / Cuerda arco 2 * ZN). [M.T.I.] Configuración de Menelao. |
Pero, inmediatamente por hipótesis, cada uno de los arcos AZ, ZN y HK son dados como cuadrantes; desde el catálogo, el arco KΘ esta dado desde la latitud de la estrella y el arco KB desde su longitud; y el arco ZH y el arco KL están dados desde la Oblicuidad de la Eclíptica demostrada [4]. Por lo tanto esta claro que, desde los arcos en cuestión, son dados el arco HA [= arco AZ + arco ZH], el arco AZ, el arco HL [= arco HK + arco KL], el arco LΘ [= arco KL + arco KΘ] y también el arco NZ. Por lo tanto el arco restante, NΘ, también será dado.
Nuevamente, dado que
| Cuerda arco 2 * ZH / Cuerda arco 2 * HA = (Cuerda arco 2 * ZΘ / Cuerda arco 2 * ΘN) * (Cuerda arco 2 * NL / Cuerda arco 2 * LA), [M.T.II.] Configuración de Menelao. |
Y, por lo anterior, [también] son dados los arcos en cuestión, el arco ZH, el arco HA, el arco ZΘ [= arco ZN – arco NΘ] y el arco ΘN, y el arco LA desde el arco KB por medio de [los arcos del] Ecuador que salen conjuntamente con [aquellos de la] Eclíptica en la Esfera Recta, el arco restante, NL, también será dado. Similarmente [por medio de los tiempos de salida en la Esfera Recta] el arco MB de la Eclíptica será dado desde el arco NA, [que es] la suma [del arco NL + arco LA].
Además los puntos sobre el Ecuador y sobre la Eclíptica que salen o se ponen simultáneamente con una estrella fija pueden ser hallados fácilmente por medio de las "culminaciones simultáneas", de la siguiente manera:
Sea ABGD [Fig. 8.2] un círculo Meridiano, AEG un semicírculo del Ecuador alrededor del polo Z, y BED un semicírculo del Horizonte. Sea la estrella que esta saliendo [ubicada] en el punto H del Horizonte, y dibujar ZHΘ [siendo] el cuadrante del gran círculo a través de los puntos Z y H.

Entonces de nuevo, dado que [dos] arcos ZΘ y EB del gran círculo han sido dibujados para encontrarse con los arcos AZ y AE del gran círculo,
| Cuerda arco 2 * ZB / Cuerda arco 2 * BA = (Cuerda arco 2 * ZH / Cuerda arco 2 * HΘ) * (Cuerda arco 2 * ΘE / Cuerda arco 2 * AE), [M.T.II.] Configuración de Menelao. |
Pero, de los arcos en cuestión, el arco ZA, el arco ZΘ y el arco EA cada uno comprende un cuadrante, el arco ZB [y por lo tanto el arco BA = arco ZA – arco ZB] esta dado desde la Elevación del Polo, y el punto Θ del Ecuador y el arco ΘH [y por lo tanto el arco HZ = arco ZΘ – arco ΘH] desde la "culminación simultánea". Por lo tanto el [arco] restante, ΘE, será dado.
Dado que también, las "puestas simultáneas", pueden ser fácilmente observadas tal que si cortamos un arco, ΘK, por adelante de Θ e igual al arco ΘE, la estrella se pondrá conjuntamente con el punto K del Ecuador.
Ya que en esta situación la puesta toma lugar en un arco [del horizonte medido desde el meridiano] igual al arco BH, y corta un ángulo por adelante del meridiano igual a aquel establecido hacia atrás [de él] por el arco AZ y el arco ZΘ en la presente ubicación.
Además, de los arcos del Ecuador y de la Eclíptica que salen y se ponen conjuntamente los cuales hemos calculado para cada Clima (Libro II Capítulo 8), inmediatamente será dado ese punto sobre la Eclíptica que sale junto con el punto E del Ecuador y con la estrella, y ese punto que se pone junto con el punto K y con la estrella. Esta claro que en el instante cuando el Sol esta exactamente en esos puntos de la Eclíptica, allí comenzarán a pasar (ocurrir) las salidas, las culminaciones y las puestas de la estrella fija [en cuestión] tomadas con respecto al centro del Sol, que son las llamadas “posiciones cardinales simultáneas verdaderas” [5].
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Libro VIII |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
Notas de referencia
- ↑ Ver HAMA 32-4, 39.
- ↑ En Libro I Capítulo 13, Libro I Capítulo 16 y Libro II Capítulos 7 y 8.
- ↑ La versión de Heiberg de la Fig. 8.1, derivada del manuscrito A, es defectuosa dado que contiene un punto redundante Ξ. Sigo la versión correcta del manuscrito D y del Ar.
- ↑ El arco ZH = ε, el arco KL = δ del punto K.
- ↑ , cf. Libro VIII Capítulo 4, nota de referencia nro. 6, sobre .
