Almagesto: Libro VIII - Capítulo 06
| Capítulo Anterior | Contenidos | Ir al Libro IX - Capítulo 01 |
{Sobre la Primera y la Última visibilidad de las Estrellas Fijas}
Sin embargo, en el caso de la primera y de la última visibilidad [de las estrellas fijas], encontramos que el método geométrico expuesto [anteriormente] utilizando solo sus posiciones [en latitud y en longitud] no es el más adecuado. Porque no es posible [2] encontrar el tamaño (la longitud) del arco por el cual el Sol debe estar distanciado por debajo del horizonte con el propósito de que dada una estrella tenga su primera o última visibilidad por métodos similares a los procedimientos geométricos por [medio] de lo cuales, por ej., uno demuestra el punto sobre la Eclíptica con el que esta estrella sale. Dado que este arco (el arcus visionis [3]) no puede ser el mismo para todas las estrellas ni el mismo para una estrella dada en todos los lugares [de la Tierra], sino que varía de acuerdo a la Magnitud de la estrella, su distancia en latitud desde el Sol, y el cambio en las inclinaciones de la Eclíptica (con respecto al Horizonte).
Ya que si imaginamos ABGD un círculo Meridiano [Fig. 8.3], AEZG un semicírculo de la Eclíptica, y BED un semicírculo del horizonte alrededor del polo H, esta claro que, dada una estrella saliendo simultáneamente con el punto E de la Eclíptica [4], [y] si una estrella de mayor magnitud tiene su primera visibilidad cuando el Sol esta a una distancia de, por ej., el arco EZ por debajo de la Tierra [(del horizonte)], una estrella de menor magnitud, incluso una a una igual distancia en latitud desde el Sol, tendrá su primera visibilidad cuando el Sol esta a una mayor distancia que la del arco EZ, y [por lo tanto] el efecto de sus rayos será más débil.
Nuevamente, para las estrellas de igual magnitud, si una estrella que esta más cerca, en latitud, al punto E tiene su primera visibilidad a una distancia [del Sol desde el horizonte igual] al arco EZ, [y] una estrella que esta mas lejos que ese [punto E en latitud] tendrá su primera visibilidad a una distancia [solar] menor. Ya que dada la misma distancia del Sol por debajo del horizonte, los rayos en la vecindad de la Eclíptica y del Sol mismo son más densos [5] que aquellos más alejados.
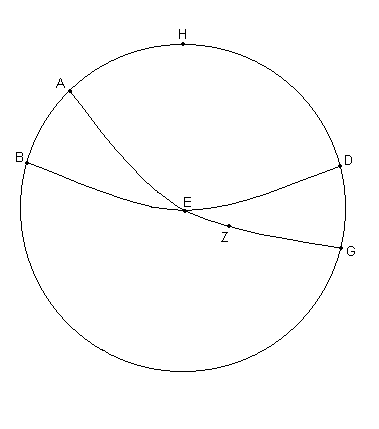
[Finalmente], en el caso de las estrellas de igual magnitud que salen a iguales distancias, en latitud,[desde el Sol], cuanto más este la Eclíptica inclinada al horizonte, [por ende] haciendo un ángulo DEZ más pequeño, mayor [será la] distancia [solar] EZ en la cual la estrella tendrá su primera visibilidad.
Dado que si, como en la siguiente figura [Fig. 8.4], también dibujamos HΘZK en el semicírculo a través de los polos del horizonte y del Sol en Z [6], el cual será, obviamente, perpendicular al horizonte, la distancia [vertical] del Sol por debajo de la Tierra siempre permanecerá igual a ZΘ para la misma estrella, dado que, para un intervalo tomado igual [(de la misma longitud)], el [efecto] de los rayos por encima de la Tierra será similar; pero si el arco ΘZ se mantiene constante, el arco EZ, como dijimos, llegará a ser menor tanto como la Eclíptica salga más en una posición perpendicular, y mayor, tanto como ésta [la Eclíptica] este más inclinada [7] [en el horizonte].
Por lo tanto necesitamos observaciones para cada una de las estrellas fijas individuales con el fin de determinar la distancia [requerida] del Sol por debajo de la Tierra medida a lo largo de la Eclíptica. Y si incluso la distancia vertical al horizonte (por ejemplo, en la figura presente [Fig. 8.4], ZΘ) no sigue siendo la misma para las mismas estrellas en todos los lugares de la Tierra, dado que los rayos de similar densidad no tienen el mismo efecto de oscurecimiento [8] en el aire más espeso de las latitudes terrestres más al Norte (septentrionales), necesitaríamos observaciones, no meramente en una latitud terrestre, sino que en cada una de las otras [latitudes] por igual. No obstante, si el arco correspondiente a ZΘ permanece constante en todas las partes de la Tierra para las mismas estrellas (como parece probable, dado que las estrellas fijas también deben estar afectadas por la variación en la atmósfera del mismo modo que para los rayos), las distancias observadas en una única latitud terrestre nos serán suficientes para determinar aquellas en las otras latitudes: [podemos hacer esto] por métodos geométricos, si la variación en la inclinación de la Eclíptica es debida al lugar terrestre [de observación] o al movimiento demostrado de la esfera de las estrellas fijas hacia atrás con respecto a ella [a la Eclíptica].
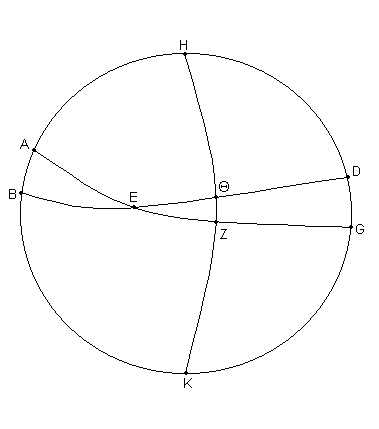
[Para demostrar esto], en la figura descrita [Fig. 8.4.], sea EZ la distancia dada desde una observación en cualquier latitud terrestre sea cual fuere. Entonces, nuevamente, dado que los [dos grandes arcos del círculo] BΘ y ZA han sido dibujados para encontrarse [con] los dos grandes arcos del círculo HB y HZ,
| Cuerda arco 2 * AB / Cuerda arco 2 * BH = (Cuerda arco 2 * AE / Cuerda arco 2 * EZ) * (Cuerda arco 2 * ZΘ / Cuerda arco 2 * ΘH), [M.T.II.] Configuración de Menelao |
Pero, de los arcos en cuestión, el arco BH y el arco ΘH son [dados] inmediatamente, [siendo] cada uno de un cuadrante [de 90°]; y dado que el punto E esta dado por hipótesis, con el cual la estrella sale, también es dado A el punto culminante, por medio de la sección sobre los tiempos de salida (al final del Libro II Capítulo 9): por lo tanto el arco AE también esta dado de esta manera, y el arco EZ por la observación; y también el arco AH [y en consecuencia también es dado el arco AB = arco BH – arco AH], siendo derivado de la distancia del punto A desde el Ecuador (que esta dada desde la Tabla de la Inclinación (de la Eclíptica)) y de la distancia del Ecuador desde el Cenit a lo largo del mismo Meridiano (que es igual a la elevación del polo). Por lo tanto el [arco] restante, ZΘ, será dado.
Una vez que este [arco ZΘ] ha sido hallado, y sigue siendo siempre el mismo para todos los lugares, desde las mismas consideraciones podemos utilizarlo para derivar las cantidades del arco EZ para [todas] las otras latitudes terrestres. Nuevamente [en Fig. 8.4]
| Cuerda arco 2 * HB / Cuerda arco 2 * AB = (Cuerda arco 2 * HΘ / Cuerda arco 2 * ZΘ) * (Cuerda arco 2 * ZE / Cuerda arco 2 * EA), [M.T.II.] Configuración de Menelao |
Y, de los arcos en cuestión, ahora el arco ZΘ esta dado por hipótesis; y dado que E, el punto que sale conjuntamente con la estrella en la latitud terrestre en cuestión, esta dado por el procedimiento demostrado anteriormente (al final del Libro VIII Capítulo 5), y similarmente son dados los arcos EA y BA [9], el arco restante EZ, que es el arco de la Eclíptica, también es dado.
Daremos por sentado el mismo método de operación para las últimas visibilidades, que ocurren cerca del punto de la puesta. Prácticamente la única diferencia será que en la misma figura [Fig. 8.4] la Eclíptica será dibujada sobre el otro lado [de BED], de acuerdo con la manera en que se inclina cuando el [arco] del horizonte BD es tomado como parte occidental [ver Fig. N].

Pensamos que lo anterior es suficiente como una indicación de los métodos en este tipo de investigación teórica, suficiente [al menos] para que no se pueda decir que hemos descuidado este tema. Sin embargo, viendo que el cálculo de este tipo de predicción es de gran complejidad, no solo por el gran número de diferentes latitudes terrestres e inclinaciones de la Eclíptica involucradas, sino también debido a la gran multitud [(cantidad)] de estrellas fijas; viendo, también, que, con respecto a las presentes observaciones de las fases [10] es laborioso e incierto, dado que [las diferencias entre] los mismos observadores y la atmósfera en las regiones de observación pueden producir variaciones en y debido alrededor de la hora de la primera supuesta ocurrencia, como ha quedado claro, por lo menos a mí, desde mi propia experiencia y desde las discrepancias en este tipo de observaciones; viendo, además, que debido al movimiento de la esfera de las estrellas fijas [a través de la Eclíptica], incluso para las latitudes terrestres individuales, las salidas, culminaciones y puestas simultáneas no pueden permanecer siempre idénticas con las presentes, lo que tomaría una gran cantidad de cálculos numéricos y geométricos para calcularlas, hemos decidido prescindir de una operación de este tipo [que] requiere mucho tiempo. Por el momento nos conformamos así mismos con las [fases] aproximadas las cuales pueden ser derivadas tanto desde [11] los registros iniciales [12] [más antiguos] o tanto desde la manipulación actual del [Globo de las Estrellas] para cualquier estrella en particular. Además, notamos que los pronósticos concernientes a los estados de la atmósfera derivados desde las primeras y últimas visibilidades (si incluso uno asigna a esta como causa [de los cambios en el clima], y no más bien a las posiciones [del Sol] en la Eclíptica), son casi siempre aproximaciones, y no exhiben una regularidad perfecta e invariabilidad: parece que este factor casual tiene solamente una aplicación general, y deriva su vigencia (fortaleza), no tanto desde la hora actual de la primera y de la última visibilidad, sino que a partir de las configuraciones con respecto al Sol, tomadas a intervalos en números redondos [enteros], y, en parte, a las inclinaciones [13] de la Luna en esas configuraciones.
| Capítulo Anterior | Contenidos | Ir al Libro IX - Capítulo 01 |
| Libro VIII |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
Notas de referencia
- ↑ Ver HAMA II 927-8.
- ↑ Leer en el manuscrito en H198,18. Heiberg elimina , dado que uno espera un verbo indicativo. Aunque para el infinitivo después de las palabras como en oratio oblicua ver Kühner-Gerth II 551, dado por Jenofonte, Mem. 1.2.13, ... .
- ↑ Nota del traductor al español: El arco visual (del latín, arcus visionis) especifica la distancia mínima entre el Sol y otro objeto celeste, que es necesario para observar su salida o su puesta en posición helíaca (orto helíaco) y salida acrónica (el cuerpo celeste sale cuando el Sol se pone).
Por definición, es la profundidad del Sol medida perpendicularmente debajo del horizonte en el momento en que el objeto celeste llega al horizonte. El arco visual tiene diferentes valores para cada objeto celeste y para diferentes lugares de observación, ya que diferentes factores, como la magnitud aparente de la estrella, su desaparición y las condiciones atmosféricas influyen en el arco visual. Por ejemplo, la contaminación del aire y la contaminación lumínica en el área de una gran ciudad pueden aumentar considerablemente el arco visual necesario para percibir una estrella.
Una fórmula de aproximación de uso frecuente para el arcus visionis es: 10,5° + 1,4° * Magnitud Aparente del objeto celeste.
Fuente Sehungsbogen.
- ↑ Ptolomeo dice “de aquellas estrellas que salen simultáneamente con el punto E”. Sin embargo, no quiere dar a entender comparar un número de estrellas saliendo simultáneamente con algún punto fijo de la Eclíptica; dado que ello no permitiría la tercera situación prevista, en la que dos estrellas diferentes con la misma latitud cruzan el horizonte junto con el punto E, y el ángulo en E siendo diferente en los dos casos.
- ↑ Literalmente “más numeroso”.
- ↑ Tomando la lectura en el manuscrito D en H200, 6, Z (en cambio de Z), y en H200,7, HΘZK (también en el manuscrito Ar) en cambio de ΘZK. Corregido por Manitius.
- ↑ Leer (en el manuscrito D) en cambio de en H200,13.
- ↑ , “brilla para oscurecer”. Ver el Libro X Capítulo 1, nota de referencia nro. 8.
- ↑ Como antes, (Fig. 8.4), desde [el punto] E, el horóscopo, por el procedimiento al final del Libro II Capítulo 9 encontramos A, el punto culminante. Por lo tanto tenemos el arco EA. El arco AB = arco BH – arco AH, donde el arco BH = 90º y el arco AH = φ – δ (A).
- ↑ Leer ' , en el manuscrito D, en H203,14, por ej. tomándola como la siguiente [palabra] y entendiendo antes . Heiberg imprime () ; posiblemente entendiendo antes de ella, pero esta es [una palabra] muy áspera. Por "fases" () Ptolomeo da a entender aquí ambas visibilidades, la primera y la última.
- ↑ Leer , en el manuscrito D, en cambio de ' en H204, 3.
- ↑ En su última obra, Phaseis, donde en el cual solo el Libro II es conservado, Ptolomeo lista varios de estos [registros].
- ↑ . Desde el Tetrabiblos (II 13, ed. Boll-Boer 100,7-9) parece que Ptolomeo quiere decir la dirección ("viento") hacia la cual apunta la Luna en su movimiento en [argumento] de la latitud. Sino ver también ibid. (Tetrabiblos) II 14, 5 (ed. Boll-Boer 102,2-3) donde esta parece ser la dirección hacia la cual apunta la “hoz” o los puntos de la Luna gibosa.
