Ir al contenido

Almagesto: Introducción

Añadir enlaces
De Wikisource, la biblioteca libre.
Ir al Prefacio Contenidos Ir al Libro I - Capítulo 1

Ptolomeo

Se conoce poco para hacer una descripción detallada de la vida del autor del Almagesto y de otros de sus numerosos trabajos tales como los de astronomía, astrología, geografía, óptica y de otros temas matemáticos; doy una referencia al lector en mi artículo “Diccionario de Biografías Científicas”, (Toomer [5]). Aquí solo hago mención de su nombre que es Claudius Ptolemaeus (Κλαύδιοζ Πτολεμαῑοζ), que vivió aproximadamente desde el año 100 después de Cristo al 175 d. C. y que trabajó en Alejandría, ciudad principal grecorromana en Egipto (ocupada por estos), y entre otras cosas tuvo la mejor biblioteca del mundo antiguo.

El Almagesto

El Almagesto fue fechado con seguridad, en el reinado del emperador romano Antonino Pío (138-161 d. C.). La última observación astronómica descrita en él es la datada el 2 de Febrero de 141 d. C. (Libro IX Capítulo 7). Ptolomeo toma como referencia el comienzo del reinado de Antonino Pío como período de realización de su Catálogo de Estrellas (Libro VII Capítulo 4). Es claro también que a Ptolomeo le ha llevado mucho tiempo escribir su obra y que es producto de su plena madurez (sus propias observaciones van desde el 127 d. C. al 141 d. C., ver Tabla Cronológica de las Observaciones); considerado siempre como su primer trabajo extenso debido a los meticulosos cambios que realizó en él y a las referencias sobre el mismo en otros trabajos propios (ver Toomer [5] para mayores detalles). Sin embargo, un reciente descubrimiento por parte de Norman T. Hamilton (IV, 51) ha demostrado que la “Inscripción Canóbica” representa un paso en el desarrollo de la teoría astronómica de Ptolomeo previa al Almagesto. Dado que Ptolomeo comenzó su labor en el año décimo del reinado de Antonino Pío (146/7 d. C.), el Almagesto pudo haber sido publicado efectivamente a principios del año 150 d. C.

Como lo indica su nombre en griego, μαθηματικἡ σὐνταξιζ, ”sintaxis del tratado de matemáticas”, el Almagesto es una exposición completa de las matemáticas astronómicas tal como los griegos comprendían por este término. También existieron algunos trabajos comparables (por ej. tratados astronómicos comprehensivos) antes de que este fuera conocido. No obstante, su suceso contribuyó a la pérdida de la mayoría de los trabajos de los científicos predecesores a Ptolomeo, como sucedió con Hiparco de Nicea (Rodas) a finales de la edad antigua, porque siendo obsoletos, fueron mermando respecto de las copias. Se considera que los trabajos de Hiparco fueron utilizados igualmente por los contemporáneos Ptolemaicos más jóvenes, tales como Galeno y Vettius Valens [1], en el inicio del Siglo IV, (y probablemente mucho antes) [2], y cuando Pappus escribió su comentario acerca de él, el Almagesto había empezado a ser el libro de enseñanza astronómica, el cual permaneció por más de mil años. Por lo tanto su importancia es para nosotros, no solo como objeto de valor histórico por las observaciones y sus teorías, sino principalmente también por su influencia en toda la astronomía desde los inicios de la edad antigua y en las épocas medievales (en las áreas del Islamismo y del Cristianismo) hasta el S. XVI. Esta obra fue dominante por un gran período de tiempo la cual fue insuperable por cualquier otro trabajo excepto por los Elementos de Euclides.

Aquí no se puede intentar hacer una reseña histórica sobre su influencia [3]. Solo menciono algunos puntos en los cuales haré referencia en las notas a lo largo de la traducción. La posición del Almagesto como libro estándar de astronomía en los “estudiantes avanzados” de Alejandría (y sin dudas en los de Atenas y Antioquía a fines de la antigüedad), es ampliamente comprobable tal parcialidad existente, dada por los comentarios de Pappus (c. 320 d. C.) y por Teón de Alejandría (c. 370 d. C.). A finales de los S. VIII y S. IX, y con el interés en el crecimiento de la ciencia griega en el mundo islámico, el Almagesto fue traducido primero al siríaco, luego varias veces más, al árabe.

A mediados del S. XII no menos de cinco tales versiones estaban en manos del amateur ibn as-Salah: una traducción al siríaco, dos versiones hechas bajo el califato de al-Ma’mum (una más antigua realizada por al-Hasan ibn Quraysh, y otra fechada 7/827 por al-Hajjaj), una versión del famoso traductor Abū Yaʿqūb Isḥāq ibn Ḥunayn (c. 879-90), y una revisión de esta última por Thābit ibn Qurra ibn Marwán al-Sabi al-Harrani (c. 901) [4]. Dos de éstas traducciones están hoy disponibles, aquellas de al-Hajjaj y la de Isḥāq-Thābit [traducción de Abū Yaʿqūb Isḥāq ibn Ḥunayn revisada y reescrita por Thābit ibn Qurra ibn Marwán al-Sabi al-Harrani].

En ellas encontramos el título del tratado de Ptolomeo, dado como “al-mjsty” (solo su parte consonante). Este es indudablemente derivado de la forma griega μεγιστιζ (συνταξιζ), cuyo significado es “el más grande (tratado)”, pero finalmente esta mal vocalizado como al-majasti, que se deriva luego al latín como “almagesti”, “almagestum”, que son los antecesores de la moderna designación “Almagesto”. La evidencia disponible ha sido discutida y ensamblada por Kunitzsch en el Der Almagest 115-25, el cual hizo una buena suposición acerca de que la forma arábiga fue derivada no directamente del griego sino de una traducción del Almagesto del persa medio (Pahlavi). Por lo tanto existe una evidencia independiente de una traducción más temprana, realizada al inicio del reinado del rey sasánida Shahpuhr I (241-272), último rey persa, siendo para mí muy dudosa.

Mientras el trabajo de Ptolomeo en lengua griega original continuó siendo copiado y estudiado en el oriente del imperio Bizantino (Esteban de Alejandría, Simeon Seth, Anna Komnene, Teodoro Pródromo, Miguel Glycas y Teodoro Metoquita y otros astrónomos bizantinos), todo conocimiento sobre él fue perdido en la región occidental de Europa en la Edad Media. Las traducciones de los textos griegos al latín también fueron realizadas en la edad media, [la traducción más temprana fue realizada en Sicilia en el año 1160] [5], la principal vía para el restablecimiento del Almagesto en el Occidente Europeo fue la traducción desde el árabe por Gerardo de Cremona, hecha en Toledo y completada en 1175 [6]. Manuscritos del texto griego comenzaron a llegar al Oeste en el S. XV, pero el texto de Gerardo de Cremona le dio vitalidad a los libros de astronomía, (muchas veces con varias eliminaciones del texto), como ocurre en el sumario inicial de Peurbach-Regiomontanus del Almagesto (ver en la Bibliografía sobre Regiomontanus). También esta fue la versión que por primera vez fue impresa (Venice, 1515). El S. XVI, vio la amplia diseminación del texto griego, (impresa en Basilea por Hervagius, 1538), y también el obsoleto sistema Ptolemaico, incluyendo no mucho, las teorías de los trabajos de Copérnico (cuyas formas y conceptos eran aún dominados por el Almagesto) como también los de Brahe y Kepler.

La Traducción

La base de mi traducción es la del texto griego, establecida por Heiberg. Dada la oportunidad, tuve que recurrir a él para hacer cientos de correcciones al texto. Esto ocurrió en los lugares (frases) donde la traducción fue realizada [7], y tales correcciones han sido listadas en el apéndice B (no presente en esta traducción al español). En muchos casos implican varios cálculos astronómicos, y mi corrección consiste en adaptar la lectura del manuscrito D, injustamente despreciado por Heiberg, como descendiente de un arquetipo debido a la revisión crítica alejandrina de finales de la antigüedad (Prolegomena, en Ptolomeo, “Opera Minora” CXXVI – VII). Sea cual fuere la verdad acerca de todo esto, y sobre el menosprecio hacia él, Heiberg dijo: “es el más negligente que se ha escrito”, yo estoy convencido ciertamente que su consistencia interna representa una tradición sólida como la existente en los manuscritos A, B y C, generalmente preferidos por Heiberg. En muchos casos sus lecturas obvias corregidas son compartidas en su totalidad o en parte por la tradición árabe. No obstante, no me he desviado del texto de Heiberg excepto dónde me pareció que ha habido alguna inconsistencia numérica. Haciendo correcciones hice referencia a las fotografías (microfilms) de los siguientes manuscritos:

En el manuscrito griego, donde utilicé la notación de Heiberg [basada, a su vez según su prólogo, en los manuscritos: Codex Parisinus Graecus (A) 2389 y (F) 2390, Codex Vaticanus Graecus (B) 1594, (D) 180 y 184, Codex Marcianus Graecus (C) 313 y (E) 310].
En el (A), del Parisinus graecus 2389. Principalmente las letras tipo uncial, del S. IX.
En el (B), del Vaticanus Graecus 1594. Minúsculas, del S. IX.
En el (D), del Vaticanus Graecus 180. Varias correcciones, pero no como las de Heiberg, Almagesto I p. V, del S. XII, a veces del S. X: ver el catálogo del Vaticano de Mercati, Iohannes y Franchi de' Cavalieri, Pius, I p. 206. Nigel G. Wilson ha hecho una inspección confirmando personalmente estas fechas dadas por mí. (El propio Heiberg parece que cambió su opinión más tarde: ver Prolegomena LXXIX).
En el arábigo (he utilizado las abreviaciones “Ar” para referirme a una relación con la tradición árabe, e “Is” al manuscrito según la versión de Isḥāq-Thābit).
En el (L), Leiden 680. Del S. XI de acuerdo a Kunitzsch, “Der Almagest” 38. Esta es la única versión del manuscrito según la versión de al-Hajjaj .
En el (T), Tunis, Bibliotheque Nationale, 07116 (ver Kunitzsch, “Der Almagest" 38-40). Completada en Octubre de 1085. Es la versión de Isḥāq-Thābit completa.
En el (P), Biblioteca Nacional de París, ar 2482. Completada en Diciembre de 1221. Ver Kunitzsch, “Der Almagest” 42-3. Es la versión de Isḥāq-Thābit, libros I-VI 13.
En el (Q), B. N. de París, ar. 2483. Del S. XV. Ver Kunitzsch, “Der Almagest” 43. Es la versión de Isḥāq-Thābit, libros I-VII 13.
En el (E), de Biblioteca de El Escorial 914. Ver Kunitzsch, “Der Almagest” 43-4. Es la versión de Isḥāq-Thābit, libros V-IX.
En el (F), de El Escorial 915. Completado en Septiembre de 1276. Ver Kunitzsch, Es la versión de Isḥāq-Thābit, según se afirma conteniendo los libros VII-XIII, pero carente, en efecto, de grandes secciones iguales a este y un desorden tal, siendo de poco uso.
En el (Ger), la traducción latina de Gerardo de Cremona, donde he utilizado solo la edición impresa (Venice, Liechtenstein, 1515. Ver Kunitzsch, “Der Almagest”, 97-104) para una relación o dependencia compleja de este con varias versiones arábigas.

No he emprendido una comparación completa entre algunos de los manuscritos mencionados más arriba. El manuscrito griego, (que le he dado poco uso) y en todas las ediciones de los informes de Heiberg, son muy precisos (a juzgar de mis esporádicas verificaciones; las remarqué en las notas de la traducción). Para comparar la traducción de este libro con las del árabe debería haber demorado varios años más, pero no le he proporcionado más tiempo. Consulté los manuscritos mencionados arriba solo en los pasajes donde consideré o supuse que el texto de Heiberg era erróneo. De cualquier modo no se hicieron notas acerca de la lectura del manuscrito árabe, donde tampoco no las informé explícitamente. Existen un gran número de lugares donde sí consideré que el texto griego difiere del de Heiberg y sobre lo cual también no me he molestado en registrarlo en este libro.

Por ej.: principales correcciones de ortografía que hice:

ηύρίσκομεν por εύρίσκομεν (imperfecto) I 327,15
Κάλλιπποζ por Κάλιπποζ I 199,5
άμετάπειστον por άμετάπιστον I 6,18 (cf. Boll, Studien 74)
κρίκοζ por κρικοζ I 196,8

Cambios en formas que no afectan el sentido: αν por έάν I 393, 11
Reversión de las letras refiriendo figuras: ZK por KZ I 243, 22

Errores obvios de impresión:
σελήνζ por σηλήνηζ
άνωμαλίαζ por άμωμαλίάζ I 462, 19

(Otros errores menores (obvios) de impresión son registrados, particularmente aquellos que involucran números).

Durante el transcurso de la traducción comencé convencido de que el texto contenía gran número de interpolaciones, (las cuales deben revisarse según los manuscritos de la era antigua), y en donde se encuentran a lo largo de todo el manuscrito de la tradición árabe y de la griega. Fui el primero en llegar a estas conclusiones, por el descubrimiento de que ellas se hallan en lugares no esenciales del texto como se presentan, las cuales fueron escritas para proteger el perfecto sentido (del texto) y simplemente eliminando una cláusula o sentencia, que pudieron haber sido insertadas como expresiones de alguien quien erró el entendimiento de Ptolomeo. Un ejemplo notable es en el Libro V Capítulo 1 y también en el Libro V Capítulo 12. Más tarde lo hice en aquellas siendo tipos de elementos completamente textuales que deben ser considerados también como interpolaciones. Una de éstas interpolaciones son los totales en el catálogo de estrellas. Las otras son los encabezamientos de los capítulos los cuales no son aptos como para describir un contexto presente del capítulo, siendo improbable atribuírselas a Ptolomeo. En efecto, no creo que Ptolomeo, propiamente dicho, haya utilizado alguna división de capítulos en general. Es obvio que él es el responsable de la división dentro de 13 libros, tal como se encuentran en los sumarios al comienzo de muchos libros y como referencias explícitas, como en el Libro I Capítulo 1 (έν τω πρώτω τηζ συντάξεωζ, Libro II Capítulo 1) y en el “libro precedente” (έν τω πρό τούτων συντάγματι, Libro VI Capítulo 5). Él nunca se refirió a una división de capítulos. Además, aquí existe una discrepancia, en la tradición del manuscrito (especialmente entre la rama representada por el manuscrito D y la representada por el A), referida a los puntos de división entre capítulos (por ej. al principio del Libro III), y también en los comentarios de Pappus, es claro que existió en ese período una división entre capítulos, siendo diferente al comienzo del Libro V y con respecto de la presente división [8]. Si la división de capítulos y encabezamientos son ilegítimos, entonces también debe ser la tabla de contenidos precediendo cada libro. No obstante, ya que este método de subdivisión del texto es bien utilizado para diferentes propósitos, y aparece en todas las ediciones, también tuve que hacerlo principalmente remarcando el carácter de los encabezamientos del capítulo encerrándolos entre llaves.

TRADUCCIONES DIGITALIZADAS:

Que es el Almagesto y que no es

Es completamente lógico el orden de cómo estudiar (todos) los temas en el Almagesto (esbozado en el Libro I Capítulo 2). En el Libro I, después de un breve tratado sobre la naturaleza del universo (en la medida como se expresa el astrónomo), Ptolomeo desarrolla la teoría trigonométrica necesaria para la obra en su totalidad. En el Libro II Ptolomeo discute aquellos aspectos de la astronomía esférica los cuales son descritos para la posición de un observador (ubicado) en la Tierra (horas de salida, cantidad de luz diurna, etc.). El Libro III esta dedicado a la teoría del Sol. Es prioritario el tratado de la Luna que se describe en el Libro IV, ya que en el cálculo de los eclipses lunares, se toma en cuenta la habilidad de uno para calcular la posición del Sol. El Libro V trata la teoría avanzada de la Luna, que es un refinamiento con respecto a la del Libro IV, tratando también las paralajes lunares y solares. El Libro VI trata sobre los eclipses, y requiere por lo tanto del conocimiento de la teoría solar y lunar, como también de las paralajes. Los Libros VII y VIII tratan las estrellas fijas: dado que la Luna es tomada en cuenta como “marcador” para determinar la posición de algunas estrellas cruciales, la teoría lunar debe preceder a ello, y algunas observaciones planetarias están realizadas con respecto a las estrellas fijas, y el establecimiento de un catálogo de estrellas (Libro VII Capítulo 05 y Libro VIII Capítulo 01) debe preceder a la teoría planetaria. Los últimos cinco libros están dedicados a los planetas. Los libros IX al XI desarrollan la teoría de sus movimientos longitudinales, el Libro XII trata los movimientos retrógrados y las grandes elongaciones (que dependen solo de la longitud), mientras que el Libro XIII considera la latitud planetaria y todos aquellos fenómenos los cuales parcialmente dependen de ella (por ej. las fases). Más tarde Ptolomeo anticipa ocasionalmente los resultados por motivos de conveniencia (ver Libro IV Capítulo 03 y Libro IX Capítulo 03), donde el movimiento medio en las tablas de la Luna y de los planetas incorporan más tarde (también) correcciones, pero en general el orden de presentación, dentro de los libros tanto como en la totalidad del tratado, esta dedicado con una lógica de metodología didáctica.

De cualquier modo, hay ciertos temas que Ptolomeo no los discute ya que los toma como garantía de que son conocidos por sus lectores, o porque le parecen superfluos para entrar en detalles (me refiero especialmente a los temas cronológicos). Advirtió especialmente (Libro I Capítulo 1 nota de referencia nro. 10) que la obra “es para aquellos que tienen algunos conocimientos en el campo”, esto significa que en la práctica, este asume un conocimiento de geometría elemental (“Euclides”), de “lógica” (que más tarde no la considera necesaria para explicar cómo extraer una raíz cuadrada), y también de las “esféricas”. Lo último es ilustrado por los trabajos existentes de Autólico de Pitane, Euclides (“Phaenomena”), y Teodosio de Bitinia (“Spherica”), que están de acuerdo con los fenómenos derivados de la rotación de las estrellas y del Sol desde un centro, de una Tierra esférica, e.j. sus salidas, puestas, primeras y últimas visibilidades, períodos de invisibilidad, la Tierra esférica, etc., utilizando geometría elemental, pero principalmente llegando a resultados [9] cualitativos mas que cuantitativos. En la obra de Ptolomeo estos resultados son obsoletos en su mayoría, aunque él hace bastante uso de una terminología y de conceptos sobre esféricas sin explicación.

Qué es lo que el lector debe conocer del Almagesto

Generalmente el lector moderno esta familiarizado con la geometría elemental. Por lo tanto, la traducción no la he llenado con referencias a Euclides excepto donde inmediatamente se asumen los teoremas siendo no obvios. Como fuere, lo que damos como una breve explicación de los métodos, conceptos y hechos no explicados por Ptolomeo los cuales el lector necesita conocer del Almagesto y que pueden ser menos familiares. En general uno puede estudiar los métodos matemáticos de Ptolomeo consultando a Olaf Pedersen 47-56.

(a) El sistema sexagesimal

Fue adquirido por los griegos desde los Babilonios (uno puede confirmarlo a través de los astrónomos Helenísticos), como vía conveniente de expresar fracciones y (en menor medida) para los grandes números, y realizar cálculos con ellos. Este es el primer sistema de valores conocido en la historia. En las traducciones y notas, utilicé la moderna notación conveniente, donde 6,13;10,0,58 representa 6 * 60 + 13 + 10 * 60 ^ (-1) + 0 * 60 ^ (-2) + 58 * 60 ^ (-3). Ptolomeo utiliza este sistema solo para fracciones, y representa a todos los números aún cuando están combinados con las fracciones sexagesimales, por [medio de] la notación (alfabética) estándar griega. La traducción continúa esta mezcla de notación (tanto que el número descrito arriba podría ser escrito en la traducción como 373;10,0,58, y en griego seg. τογ seg. ί ο seg. νη).

(b) Fracciones

Excepto donde la fracción necesariamente sea precisa, Ptolomeo prefiere el sistema tradicional griego de fracciones para los sexagesimales. También es posible expresar fracciones propias como por ej. “4 5 tos.” [cuatro quintos], preferentemente dada en unidades de fracción, esto es por ej. “¾” es expresado como la suma de “½” y “¼” (escrito < “δ”, por ej. “½ ¼”). Hay un signo especial para ⅔. Usualmente en la traducción he convertido estas sumas de unidades de fracciones a fracciones en sí, sin comentarios. De cualquier modo, he considerado la parte de la fracción donde Ptolomeo lo ha hecho, dado que él da una falsa apariencia de precisión para convertirlas a sexagesimales (tal como hizo Manitius, escribiendo un número exacto de minutos en cambio de una fracción de un grado). Particularmente esto esta confirmado en el catálogo de estrellas.

(c) Trigonometría

La función trigonométrica exclusiva utilizada por Ptolomeo es la cuerda. La derivación y estructura de “su” Tabla de las Cuerdas esta completamente explicada en el Libro I Capítulo 10. Sin embargo Ptolomeo no da instrucciones explícitas para su uso en los cálculos trigonométricos aunque su método es suficientemente obvio en los ejemplos prácticos. Seguidamente doy una traducción literal con comentarios de un cálculo típico, teniendo en cuenta la trigonometría.

Ver la figura A, y, por mis convenciones, comparar la traducción en el Libro III Capítulo 6 Fig. 3.18. En una situación dada, el arco ΘH es de 30º, AD es de 60p, AH es 2;30p (p = partes), y es requerido para hallar el ángulo ADH (la “ecuación”). En la trigonometría moderna podríamos utilizar la fórmula del coseno. Ptolomeo no tiene equivalente, entonces elimina la perpendicular HK, así transforma el problema en una solución solo de triángulos rectángulos, siendo este su procedimiento estándar [10].

“Luego dado que el arco ΘH es nuevamente de 30 grados, el ángulo ΘAH sería de esas 30 (unidades) donde 4 ángulos rectos son 360 grados, y 60 de esas (unidades) en las que 2 ángulos rectos son 360. Entonces el arco en HK es de 60 unidades en las que el círculo (circunscrito) alrededor del triángulo rectángulo HKA es de 360, y el arco sobre AK es de 120, suplementario que forma el semicírculo. Y entonces, las cuerdas subtendidas por él, HK será de 60 de unidades cuya hipotenusa AH es de 120, y AK de 103;55 en las mismas (unidades).”

Fig. A
Fig. A
Fig. A

Para resolver el triángulo rectángulo HKA, Ptolomeo imagina un círculo circunscrito en él. Luego, la hipotenusa del triángulo es el diámetro del círculo, y es tomado, inicialmente de 120 partes; siendo 60 partes la medida estándar (patrón), a partir del cual fue construida la Tabla de las Cuerdas. Los dos ángulos agudos del triángulo son dados, los otros dos lados pueden ser expresados en la misma unidad de medida: siendo ambos las cuerdas de los arcos del círculo circunscrito, que son el doble de los ángulos del triángulo (siendo iguales a los ángulos en el centro). Ptolomeo en cambio de la explicación del doble de estos ángulos inicialmente siempre los expresa en “unidades donde dos ángulos rectos son 360”. (Siguiendo la convención inventada por B. R. Goldstein, indico estos “semi grados” por medio de la notación ºº, reservando º para el grado estándar en los que tenemos 90 para un ángulo recto). Esto le permite a él cambiar de igual forma desde un triángulo al círculo (y en consecuencia a la Tabla de las Cuerdas, que le brinda los números actuales de 60p y 103;55p): un ángulo de medida θº es igual a 2θºº, y por lo tanto el arco del círculo circunscrito que corresponde a aquel ángulo es igual a 2θº.

“Por lo tanto en esas (unidades) donde la línea AH es 2;30, y el radio AD es de 60, HK será de 1;15 y AK, igualmente, de 2;10, y el resto KD de 57;50.”

Los lados del triángulo AKH son convertidos en la norma representando sus tamaños actuales (AH = 2;30p, por lo tanto son multiplicados por 2;30/120). Esto da los dos lados del siguiente triángulo a ser resuelto, DHK / HK y (por sustracción de AK del AD dado) KD.

“Y dado que los cuadrados de estos sumados en conjunto dan el cuadrado de DH, lo último será en longitud aproximadamente de 57;51 de las unidades de las cuales la línea KH fue (hallada ser) de 1;15.”

Dado que Ptolomeo no tiene la función tangente, utiliza el Teorema de Pitágoras para hallar la hipotenusa del triángulo rectángulo en cuestión. Utiliza la palabra , “en longitud”, para indicar que esta tomando la raíz cuadrada (considerada como el lado de un cuadrado, por ende una línea de longitud).

“Y entonces de esas (unidades) donde la hipotenusa DH es de 120, la línea HK será de 2;34 y el arco en él (HK, será de) 2;27 de éstas mismas unidades donde el círculo (circunscrito) alrededor de DHK es de 360. Entonces el ángulo HDK es 2;27 de esas unidades donde dos ángulos rectos son de 360, y alrededor de 1;14 de esas unidades donde los 4 ángulos rectos son iguales a 360”.

Los lados del triángulo DHK son ahora convertidos a la [medida] estándar donde la hipotenusa es de 120p, lo que le permite a Ptolomeo utilizar la Tabla de las Cuerdas para determinar el arco HDK correspondiente al lado opuesto a ser hallado. Esto último, siendo en la circunferencia del círculo circunscrito, la mitad de arco. Ptolomeo expresa nuevamente esta relación diciendo que este es el mismo número de “semi grados” siendo el arco de “grados simples”, y luego convirtiendo los “semi grados” a “grados simples” por medio de la división. Notar que frecuentemente traduzco las expresiones como “30 grados del tipo de grados donde el gran círculo es de 360” simplemente como 30º.

(d) Cronología y calendarios

El sistema cronológico propio de Ptolomeo es muy simple. Utiliza el Año Egipcio y la era de Nabonassar. El Año Egipcio tiene una longitud invariable de 365 días, consistente de 30 días por mes y al final 5 días extras ("epagomenales").

Ptolomeo utiliza las traducciones griegas de los nombres de los meses egipcios. Para facilidad del lector usualmente agrego un número romano indicando el número del mes egipcio. El orden de los meses es:

Mes Nombre Mes Nombre
I THOTH VII PHAMENOTH
II PHAOPHI VIII PHARMOUTHI
III ATHYR IX PACHON
IV CHOIAK X PAYNI
V TYBI XI EPIPHI
VI MECHIR XII MESORE

La razón de elegir la era de Nabonassar esta descrita por Ptolomeo en el Libro III Capítulo 8: las observaciones disponibles más tempranas (Babilónicas) que describe fueron aquellas [realizadas] en del reinado del Rey Nabonassar (ver Tabla Cronológica de las Observaciones). La fecha ptolemaica, 1° de Thoth del 1° año de Nabonassar corresponde al 26 de Febrero del 747 a. C., según nuestro recuento [11].

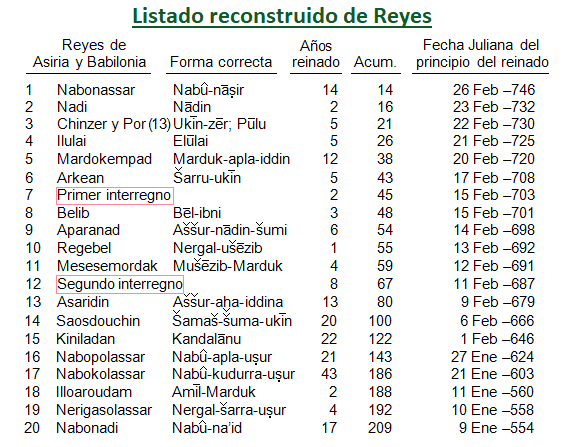
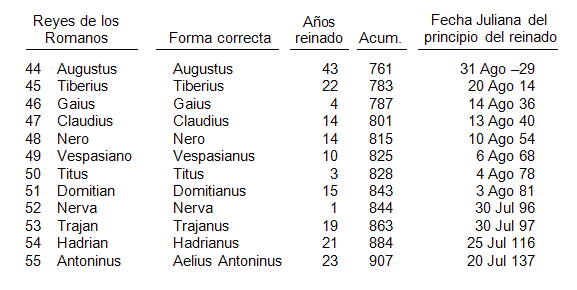
Incluso cuando Ptolomeo se refiere a otros calendarios usualmente da la fecha equivalente de la era Nabonassar, pero solo el año del reinado del rey. Esta claro que ya existía, de alguna manera, una “lista de reyes” permitiéndole a uno relacionar el año del reinado de un rey dado con la época o fecha estándar [12]. Ptolomeo más tarde publica estas “Tablas Manuales o Prácticas” como listado de reyes (conocida como “Canon Basileon”), que sobrevive en forma considerablemente aumentada en las versiones Bizantinas de Teón de Alejandría y en las revisiones alejandrinas de estas “Tablas Manuales”. De esta última tengo un extracto y seguidamente la brindo reconstruida, la cual no hace pretensiones históricas aunque sí intenta, exclusivamente, dar una clase de ayuda a los lectores de este libro. La base de la tabla es de la edición Usener desde las dos versiones del manuscrito de Leidensis gr. 78, en “Monumenta Germaniae Histórica, Auctores Antiquisimi XIII” (“Chronica Minora Saec. IV. V. VI. VII”, ed. Th. Mommsen), Vol. III, 447-53, con un suplemento de lo que he leído en el manuscrito griego del Vaticano 1291, 16v-17r. Los nombres de los reyes de Babilonia y de Asiria [13], están distorsionados (son corruptos), y no tuve la intención de repararlos, aunque tuve que elegir aquellas variantes de los manuscritos donde se leen muy próximas a las formas hoy conocidas de las tablas cuneiformes, son listadas en la segunda columna (dadas a mí por A. Sachs).[14]

A los propósitos de la cronología astronómica, es asignado un número entero de años para cada reinado. Como se puede comprobar, el “1° año” de cualquier reinado en las tablas independientes, se asume como inicio del mismo el 1° de Thoth estableciendo la fecha histórica en la que el rey comenzaba a reinar [15]. Por lo tanto, para utilizar la tabla para ir desde un reinado dado a la era Nabonassar, uno simplemente suma el número de año del reinado a la lista total (dada en la cuarta columna) del rey anterior [16]. Por ej. para hallar el segundo año de Mardokempad en la era Nabonassar (cf. Libro IV Capítulo 08), sumamos 2 años al total de los 26 años dados por su predecesor, Ilulai, y nos da el año 28 de la era Nabonassar.

También en la traducción doy el equivalente moderno de todas las fechas del Almagesto y he adicionado, para que la utilicen aquellos lectores que deseen chequearla, una quinta columna listando el equivalente juliano del primer día del reinado de cada rey. Si uno mentalmente sostiene que cada año juliano divisible por 4 es un año bisiesto, mientras que el año egipcio es constante, es una base suficiente para realizar los cálculos. Sin embargo, recomiendo como simple alternativa consultar la obra de Schram: “Kalendarigraphische Tafeln”: de la página 182-9, para que uno pueda hallar, en pocos segundos, el número del día Juliano de alguna fecha de la era Nabonassar, y por lo tanto (desde estas otras tablas) la fecha equivalente en algún otro calendario estándar. Nota del traductor al español: ver Tabla de equivalencias entre los calandarios: Nabonassar, Egipcio y Juliano-Gregoriano.

Tabla de los Reyes asirios y babilonios
Tabla de los Reyes asirios y babilonios
Tabla de los Reyes persas y macedonios
Tabla de los Reyes persas y macedonios
Tabla de los Reyes romanos
Tabla de los Reyes romanos

El otro aspecto requerido a ser remarcado son las 'fechas dobles' de la cronología propia de Ptolomeo. Él caracteriza frecuentemente el día de una observación por las expresiones tales como ' ' traducido como “17/18 de Pachon”, literalmente “del decimoséptimo día al decimoctavo día de Pachon”. Historiadores modernos innecesariamente han dado épocas confusas según lo descrito arriba. Ptolomeo utiliza en forma apropiada el período de mediodía, siendo este el punto de partida artificial (razón por la cual lo explica en el Libro III Capítulo 10), y no tiene nada que ver con la numeración del día. En la antigüedad el “tiempo civil” del día comenzaba en el amanecer en Egipto o en la puesta del Sol en Babilonia. Tanto en un sistema como en el otro, un evento que fuera observado en el día (de luz solar) pudo haber sucedido en el mismo “día”, pero uno que fuera observado por la noche pudo haber ocurrido en el “día n” del día egipcio es decir como inicio del día en el amanecer y a su vez en el “día + 1” en el babilonio, tomando el comienzo del día con la puesta del Sol. Consecuencia de ello una ambigüedad era posible. Ptolomeo utiliza fechas dobles (las cuales corresponden solamente a las observaciones nocturnas) que presentan tal ambigüedad. La forma que él utiliza implica la egipcia, por ej. el recuento desde el amanecer (cf. la forma larga en el Libro III Capítulo 02, '  seg. ' literalmente “en el decimoprimer día de Mesore, aproximadamente dos horas después de la medianoche hacia la duodécima”), aunque esto pueda ser claro incluso para alguien que utilice la época (recuento) desde la puesta (pudiendo fechar el evento de arriba como “12 de Mesore”) como día significativo.

Utilizando observaciones de sus predecesores Ptolomeo tiene la ocasión de referirse frecuentemente a otros sistemas cronológicos y calendarios. También en estos casos uno, fácilmente, puede derivarlos siempre al sistema propio de Ptolomeo (casi siempre lo da explícitamente). Seguidamente lo describiré brevemente.

El sistema mencionado más frecuentemente es el Ciclo Calípico. Para explicar este, debemos ir atrás hasta Metón (ver Ciclo Metónico), quién en el año –431 ideó un ciclo de 19 años, con, por ejemplo, un esquema fijo de intercalación de meses conteniendo 6940 días (por lo tanto el promedio de la longitud del año era 365¼ + 1/76 días) [17]. Dado que fue ateniense, utilizó los nombres de los meses de su calendario artificial. Cien años más tarde un “asociado” de Aristóteles, Calipo, realizó una revisión a éste, basado en un año más preciso (en longitud) de 365 ¼ días. En orden de lograr esto, Calipo elimina un día de los 4 Ciclos Metónicos, de ahí en más creando el “Ciclo Calípico” de 76 años ó 27759 días. Más tarde este fue conocido como el “primer Ciclo Calípico” comenzando con él en el solsticio de verano (probablemente el 28 de Junio) del año –329. En el Almagesto también encontramos referencias al segundo y tercer ciclo Calípico, que comienzan en los años –253 y –177 respectivamente. A juzgar desde el Almagesto, este sistema cronológico fue el más usado por los primeros astrónomos Helenísticos [18]. En el Libro VII Capítulo 3 cuatro observaciones atribuidas a Timocares (Alejandría, S. III a. C.) eran dadas acorde al año del primer Ciclo Calípico y al mes y día ateniense. Sobre la base de esto, varias consideraciones han sido realizadas para reconstruir enteramente el “calendario Calípico”, aunque con resultados discrepantes. Según lo descrito arriba, ello constituye una base completa de evidencia, aparte del pasaje en Geminus, “Eisagoge VIII”, que he considerado como ficción, y dos dudosas equivalencias en el parapegma Milesiano, donde cualquier reconstrucción es académica [19].

Solamente noto aquí, que Calipo evidentemente mantuvo un método peculiar ateniense para contar los días del mes por décadas, y en la última década contando hacia atrás, entonces en el Libro VII Capítulo 03 ' , literalmente “en el sexto día de la Luna menguante”, significa “el sexto día desde el final de la última década”, por ej. la vigesimoquinta [20].

Hiparco utilizó también el Ciclo Calípico para el fechado astronómico, pero combinándolo, no con el calendario Calípico “Ateniense”, sino con el calendario Egipcio, (por ej. simplemente utilizó los ciclos como un año numerado), como al principio hemos descrito brevemente en el Almagesto. Esto parece ofrecer dos ambigüedades, dado que el año Calípico comienza (o cercanamente) en el solsticio de verano, mientras que el año Egipcio es un “año erróneo”, que en tiempos de Hiparco comienza cerca del fin de Septiembre. Por lo tanto, aquí se origina la posibilidad de una discrepancia de 1 año en el recuento, para ciertas extensiones del año (si este es +1 o –1 depende de la elección de Hiparco). Una discrepancia esta firmemente atestiguada en el Almagesto Libro IV Capítulo 11, y no puede ser eliminada válidamente por unas enmiendas, sobre todo si esto ha sido realizado (por Ideler y otros) por un interés de lograr alguna consistencia. De hecho, es imposible hacer todo el fechado del Ciclo Calípico de Hiparco consistente en el Almagesto con otro, y debemos permitir dar la posibilidad de que Hiparco utilizó distintos sistemas en diferentes trabajos.

En el Almagesto tres observaciones planetarias son fechadas , “acorde con los Caldeos”, con un número de año y un mes y día de procedencia Macedonia. Los números de año muestran que la era utilizada es aquella conocida en tiempos modernos como la era Seleúcida (fechada desde el primer año del reinado de Seleuco I Nicátor, -311/-310), siendo común a través del imperio Seleúcida. Dado que las observaciones son indudablemente babilonias, la época en particular utilizada en ellas es, como es de esperar, aquella conocida por los textos sobrevivientes de la astronomía babilonia, 1° de Nisan (Abril) del –310 (los griegos bajo el imperio seleúcido utilizaron comúnmente la época del otoño del –311). El uso de los nombres de procedencia macedonia, ha sido estrictamente adquirido para demostrar que los meses lunares simplemente fueron nombrados como los meses macedonios de los griegos bajo el imperio seleúcido: si uno calcula la fecha del primer día del mes “macedonio” desde una fecha equivalente a la era Nabonassar dada por Ptolomeo, coincide (con un error de no más de un día) respecto al día calculado desde la primera visibilidad de la Luna creciente en Babilonia [21]. Aquí hay otra evidencia para asimilar los nombres de los meses [22], siendo la más firme. Un estudio externo al Almagesto sin validar es aquel del Calendario de Dionysius. Tiene un recuento de años consecutivos y meses nombrados según los signos del Zodíaco (correspondiendo, en principio, al período del año cuando el Sol se hallaba en el signo en cuestión).

Los meses confirmados son:

Tauron (♉︎)
Didymon (♊︎)
Leonton (♌︎)
Parthenon (♍︎)
Skorpion (♏︎)
Aigon (♑︎)
Hydron (♒︎)

Del análisis del Almagesto la evidencia dada por Bockh, “Sonnenkreise” 286-340, demostró que la época del calendario era la del Solsticio del año –284. Desde el 1° de Thoth (2 de Noviembre de –284), que es el comienzo del reinado de Ptolomeo de Filadelfia, se valida como finalizada [la época del calendario] según lo observado por Dionysius en Egipto. Conclusiones posteriores de Bockh, fueron que el calendario era similar al egipcio conteniendo 12 meses de 30 días, pero modificado por la introducción de seis días “epagomenales” cada cuatro años, no pudiendo ser observado como válido, especialmente teniendo algunas enmiendas en las fechas del Almagesto. Aquí una “reconstrucción”, como para el calendario Calípico, parece impuntual cuando la evidencia es escasa y la probabilidad de verificación es enteramente remota [23].

Una observación esta datada en el calendario “Bitiniano” del período imperial. Contar con otros calendarios contemporáneos de Asia menor, uno es simplemente el calendario Juliano, con diferentes nombres de meses y como primer día el cumpleaños del César Augusto, siendo el 23 de Septiembre. Ver “Greek and Roman Chronology” 174-5 de Alan Edouard Samuel para detalles y literatura.

(e) El catálogo de estrellas de Ptolomeo

La lista de las coordenadas y de las magnitudes de las principales estrellas fijas observadas por Ptolomeo tiene un problema especial para el traductor. Hay numerosas variaciones en las coordenadas en particular, y mientras uno escribe cierto número en la traducción, es a menudo difícil estar en lo correcto según los números elegidos. La solución que he adoptado (y solo en el catálogo estelar) es agregar un asterisco en algún elemento (en la longitud, latitud, magnitud, descripción o identificación) donde surja la razón al suponer que pueda ser errónea la cifra (por ej. no según lo que Ptolomeo escribió o intentó escribir) [24], sino porque hay una variación interesante en el manuscrito, o alguna inconsistencia relevante de carácter astronómico. En tales casos, doy todas las variaciones específicas, obviamente, encontrando muchas equivocadas. El lector que desee ir más allá debe consultar a Peters-Knobel (Christian F. P. Peters y Edward Knobel), obra en la que me he basado arduamente, además de ser la mejor en el tratamiento completo de este catálogo, en lo erróneo, en la necesidad de actualización y en la revisión de ciertos temas [25].

Ptolomeo lista las estrellas dentro de 48 constelaciones, y da para cada estrella:

(1) una descripción de su localización en la “figura” y (algunas veces) su brillo y color;
(2) su longitud,
(3) su latitud y dirección (al norte o al sur de la eclíptica); y
(4) su magnitud.

He seguido a mis predecesores (Manitius) agregando lo siguiente:

(a) una columna inicial dando un número consecutivo para cada estrella dentro de su constelación (hay estrellas listadas por Ptolomeo al final de algunas constelaciones y “fuera de la constelación”, por ej. no como parte de una figura imaginaria, siendo numeradas continuamente de aquellas que las preceden);
(b) una última columna dando una identificación moderna de la estrella [26]. Ciertas estrellas más pequeñas (en brillo) no las tienen, para ello doy el número del catálogo de estrellas brillantes de Yale (abreviadas “BSC”). En esta publicación los interesados pueden encontrar el número correspondiente en el “Durchmusterung”, en los Catálogos de Henry Draper o en el Boss General Catalogue. He dejado de lado toda referencia del anticuado Catálogo de Piazzi (aún usado por Peters-Knobel).

He utilizado números romanos para enumerar las constelaciones, y referirlos a estrellas individuales (a lo largo de mi traducción por la combinación de números romanos y arábigos (por lo tanto “catálogo XXXIX 2” esta referida a la segunda estrella de la constelación número treinta y nueve (Canis Minor), llamada Procyon).

Las descripciones de las estrellas poseen numerosos problemas individuales, solo algunos de ellos los he tratado al pie de página. Idealmente, debería brindar una reconstrucción de las notas de cada constelación tal como éstas aparecen en el globo de estrellas de Ptolomeo. Desafortunadamente uno no ha hecho el trabajo necesario de ensamblar y comparar toda evidencia en la literatura e iconografía de la antigüedad y en la tradición derivada del árabe (notablemente, la de al-Sufi). Este podría ser un emprendimiento interesante y valorable. Mientras tanto, si el lector necesita alguna ilustración visual, solo puedo recomendar la vieja tarea de Johann Bayer, “Uranometría”, con la precaución de que en muchos casos el posicionamiento de las estrellas en las figuras, y en los comentarios de las figuras mismas, son ciertamente diferentes a las de Ptolomeo [27]. En el caso de la orientación de las figuras, tuve que satisfacerme a mí mismo, dado que Ptolomeo las describe como si estuvieran dibujadas desde dentro del globo, como vistas por un observador situado en el centro de tal globo, y las constelaciones encarándolas hacia él. Esto esta de acuerdo con lo que Hiparco expresó (“Comm. In Arat. I 4 5”: “Todas las estrellas están descritas en constelaciones () desde nuestro punto de vista, y como si estuvieran mirándonos a nosotros, excepto aquellas que son dibujadas de perfil” , tal como lo interpreta Manitius, de quien he dudado). En este sentido es lo que debemos interpretar como “a mano izquierda”, “a mano derecha”, etc. De esto se cuenta, que en los presentes globos de estrellas las constelaciones fueron dibujadas sobre la su superficie o lado externo. Por lo tanto la orientación de las figuras fueron (en principio y en algunos casos) revertidas, lo cual podría llevar a confusión [28]. He rendido las preposiciones utilizadas por Ptolomeo indicando consistentemente las posiciones de las estrellas con respecto a las partes de las figuras del siguiente modo:

en = 
sobre = 
encima =
arriba = 
bajo = 
debajo = 
justo por encima =  + genitivo
por delante, en avance = 
por detrás, hacia atrás = 

Acerca del significado de los dos últimos términos ver mas abajo de la página en "Signo [zodiacal]". Notar que el término “trasero” nunca se usa en otro sentido sino como direccional. Para indicar las partes de atrás de una figura de un animal uso la palabra [la cola] “trasera”. Ambas longitudes y latitudes son dadas, no en grados ni en minutos, sino en grados y fracciones de grado. Esto lo he tenido en cuenta en la traducción. En muy pocas excepciones, las longitudes no son dadas con una precisión de más de ⅙º (valor que ha sido tomado implicando que el aro graduado (eclíptico) del instrumento de Ptolomeo estaba graduado solamente cada 10 minutos). Sin embargo, uno frecuentemente encuentra las fracciones ¼º y ¾º para las latitudes.

En la lista de Ptolomeo las latitudes están precedidas por la dirección ( = , “norte”; , “sur”). Lo he aclarado con un + y con un –, respectivamente.

Los rangos de magnitudes desde 1 hasta 6 (acordes al sistema que precede, ciertamente, a Ptolomeo, son solo atribuidos a Hiparco por conjeturas). Ptolomeo indica magnitudes intermedias agregándolas (después del número) , “más grande” o , “menor que” (abreviado en el manuscrito). Esto lo he suministrado con un > y con un < (antes del número) respectivamente. Ocasionalmente, para la magnitud, en cambio de un número uno encuentra, la reseña  (dada con una “f.” para “débil”) o . (para ), “nebuloso”, abreviado como “neb.”.

Peters-Knobel (ver Christian F. P. Peters y Edward Knobel) y Manitius están de acuerdo con las identificaciones donde estuvieran, usualmente me he contenido en adoptar sus opiniones donde diferían (e incluso cuando estuvieran de acuerdo, en algunos casos especiales) [29]. He chequeado cuidadosamente las posibilidades tanto como pudiera, utilizando la gran escala del “Atlas de los Cielos” de Becvar, y transformando, donde fuera necesario, las coordenadas de Ptolomeo, la Ascensión Recta y Declinación hacia una época moderna (Equinoccio de la fecha). Sin embargo, no he intentado rehacer el trabajo de Peters y Knobel a saber, recalcular la longitud y latitud de las estrellas relevantes de la época de Ptolomeo hacia estas fechas actuales (en particular utilizando valores más modernos para los movimientos propios [de las estrellas]). Por el momento hacer esto podría ser meritorio, aunque dudo si el grado de improvisación de Peters-Knobel podría justificar tal gran cantidad de cálculos. En cualquier caso, es poco probable que ello eliminara las dudas remanentes acerca de la identificación de muchas de las estrellas débiles.

En el manuscrito, al final de cada constelación son listados los números totales de estrellas de la constelación, y los subtotales por cada magnitud. En definitiva, esta descripción también es agregada en varios puntos intermedios (en el segmento Norte, en el Zodíaco, y en el segmento Sur), y los totales generales están dados al final. Estoy convencido que esto no fue realizado por Ptolomeo (quien no lo mencionó en su descripción del catálogo, Libro VII Capítulo 04). Otra indicación de lo espurio de estos pasajes es que un recuento (no separado) se realizan en los totales de las estrellas que son mayores (>) o menores (<) a cierta magnitud: todas son agrupadas con las estrellas de tal magnitud. He traducido dichos pasajes en cuestión, pero encerrados entre llaves: { }.

(f) Explicaciones de términos especiales

(i) Geométricos

por sustracción (): literalmente “la parte restante”, “residuo” (en alguna ocasión lo he especificado).

por adición (): literalmente “el total”.

Cuerda X (Crd X): cuerda del ángulo Xº (R = 60p). El griego no tiene una palabra para especificar el significado “cuerda”, pero usa el genérico  "línea recta". “Cuerda X” especifica  x , “la línea recta subtendiendo X grados”. En conexión con el Teorema de Menelao, una expresión del tipo “Cuerda arco 2 AB” representa  AB , literalmente “la línea subtendida por el doble del arco AB”.

^ por "ángulo" (utilizado por el traductor al español).

Suplementario, arco suplementario (): literalmente “el arco que es el resto del semicírculo”.

Complementario (): literalmente, “el resto del cuadrante”.

|| literalmente. “es similar a”. Utilizado en los arcos de los círculos de diferentes tamaños. Arc AB || arc GD si cada arco es la misma fracción de su círculo.

||| (): literalmente, “tiene [todos] sus ángulos iguales a”, por ej. es similar a (utilizado solo en triángulos).

≡ (): literalmente “tiene sus lados iguales a”, por ej. "es congruente a". Utilizado solo en triángulos esféricos. Algunas veces , “tiene sus ángulos y lados iguales a”.

Q.E.D. (): literalmente “Lo que se ha requerido para examinar”.

Componendo (). Expresa la operación de la suma de las proporciones: si a / b = c / d, entonces (a + b) / b = (c + d) / d.

Dividendo () (1) Usualmente expresa la operación de sustracción de las proporciones: si a / b = c / d, entonces (a - b) / b = (c - d) / d.

(2) A la vez, en el Libro XII Capítulo 01,  expresa la divisón de los números de las proporciones. Si a / b = c / d, entonces (a / n) / b = (c / n) / d.

Figura B
Figura B
Fig. B

La Configuración de Menelao y el Teorema de Menelao (es utilizado solo en los pies de página y en las adiciones explicativas). Cf. HAMA 26-9. Fig. B representa la Configuración de Menelao. M, n, r y s son cuatro grandes círculos sobre la superficie de una esfera, intersectándose uno con otro como se muestra en la figura, y se dividen dentro de partes m1, m2, etc. (entonces m = m1 + m2, n = n1 + n2, r = r1 + r2 y s = s1 + s2). En el Libro I Capítulo 10 Ptolomeo provee los teoremas:

Teorema de Menelao I Cuerda 2m / Cuerda 2m1 = Cuerda 2r / Cuerda 2r1 * Cuerda 2s2 / Cuerda 2s
Teorema de Menelao II Cuerda 2r2 / Cuerda 2r1 = Cuerda 2m2 / Cuerda 2m1 * Cuerda 2n / Cuerda 2n2

Dado que estos teoremas los desarrolló Menelao, Neugebauer los nombra como “Teorema de Menelao I” y “Teorema de Menelao II” respectivamente, y según él, abreviándolos como “M.T.I” y “M.T.II”.

(ii) Astronomía esférica

(en) la esfera recta (' ) y (en) la esfera oblicua (' ). Estos términos medievales latinos son las traducciones desde el griego, que significan respectivamente “en la esfera recta” y “en la esfera inclinada (oblicua)”. Probablemente tomados al utilizar globos celestes, estos se refieren al fenómeno que ocurre cuando el ecuador celeste es perpendicular al horizonte local (esfera recta) o inclinado hacia él en un ángulo agudo (esfera oblicua). En particular, utilizaremos los tiempos de salida en la esfera recta o en Ascensión Recta, y los tiempos de salida en la esfera oblicua o en Ascensión Oblicua, para designar respectivamente el arco del Ecuador que cruza el horizonte con un arco dado de la eclíptica (por ej. un signo del Zodíaco) en la esfera recta (por ej. en el ecuador terrestre), y en la esfera oblicua (por ej. en cualquier otra latitud terrestre).

Ecuador: representa (), literalmente “círculo de igual día”, entonces así llamado por esta razón, Ptolomeo lo da en el Libro I Capítulo 8.

Meridiano: representa (), literalmente “círculo de medio día”, (definido y explicado en el Libro I Capítulo 8). El pasaje del objeto por el meridiano es llamado Culminación. El término griego para culminar y culminación, , , significa literalmente “estando en la mitad de los cielos”. La culminación superior y la inferior son expresadas por  y , significando respectivamente “arriba de la Tierra” y “debajo de la Tierra”, y algunas veces traducidas.

Un Círculo de Altitud es cualquier círculo dibujado a través del cenit perpendicular al horizonte. Ptolomeo no tiene un término especial para esto en el Almagesto, diciendo meramente “el (gran) círculo dibujado a través del cenit (a través de los polos del horizonte)”, por ej. en el Libro II Capítulo 12, HI 166, 20-1.

Coluros: este término es utilizado por Ptolomeo solo una vez, en el Libro II Capítulo 06. Traduzco parte de la nota de Manitius en el pasaje: Dos de los círculos de declinación a través de los polos del Ecuador son nombrados “coluros” (): el coluro del solsticio, que va a través de los solsticios y por lo tanto lleva los polos de la eclíptica, y el coluro equinoccial. Estos dos coluros dividen la esfera dentro de cuatro partes iguales y divide tanto a la eclíptica como al ecuador en cuatro cuadrantes, entonces un cuadrante corresponde a cada estación del año. Ptolomeo recuenta el coluro del Solsticio como el límite de la revolución diaria en el Libro I Capítulo 08, donde sin embargo el término “coluro” no es utilizado, pero nunca menciona explícitamente el coluro equinoccial. Ambos coluros ya fueron definidos por Eudoxo (Hiparco, “Comm. In Arat. 117 ff.). El término es explicado por Achilles, “Isagoge 27” (Mass, “Comm. In Arat. 60) como sigue: “Estos son llamados coluros porque aparentan tener, en tal forma, sus colas cortadas (), dado que nosotros no podemos ver las partes de ellas comenzando desde el antártico, paralelo siempre invisible”.

Es desafortunado que tengamos que utilizar la misma palabra “latitud” para referirse a ambas: a las coordenadas celestes (perpendicular a la eclíptica) y a la coordenada terrestre la cual no tiene relación. Ptolomeo utiliza, para el término formal , y posteriormente , literalmente “inclinación”. Necesariamente comento esto cuando lo hago como por ej. con la “latitud [terrestre]”. , sin embargo, no se refiere a la coordenada como tal (para lo cual Ptolomeo utiliza la palabra , HI 68,9, , HI 101, 23 o, una vez,, HI 188,4), aunque para una “banda [sector]” específica de la Tierra donde el mismo fenómeno es observado (por ej. la longitud del día más largo (solar)). En consecuencia, en tiempos Helenísticos más tempranos, surgió la noción de la división del mundo conocido (el ) dentro de siete “clímatas” estándares ver HAMA 334 ff. II 727 ff. y Honigmann “Die sieben Klimata”). Este término es reflejado en varios lugares del Almagesto, por ej. en la Tabla en el Libro II Capítulo 13. Me refiero a los 7 paralelos estándares por medio de números romanos, por ej. el Clima IV es el paralelo a través de Rodas, donde el día más largo era de 14 ½ horas.

(iii) Refiriéndose a los objetos celestiales

Ptolomeo en su sistema explica en el Libro I Capítulo 08, que los cielos son concebidos en su totalidad rotando del Este hacia el Oeste, haciendo una revolución diaria. La dirección definida por este movimiento, y la dirección medida de él, son llamadas  (“hacia las partes fundamentales”) y  (“hacia las siguientes partes”), respectivamente. Los adjetivos correspondientes  y , también son hallados particularmente en el catálogo de estrellas, y Ptolomeo frecuentemente utiliza las frases () , “hacia las (siguientes) [partes] principales de los signos zodiacales”, para indicar la dirección del movimiento en la eclíptica. Un lector moderno puede resultarle esto confuso: dado que el movimiento normal de los cuerpos en la eclíptica es de Oeste a Este, que nosotros consideramos como un movimiento hacia adelante, por ej.: de un planeta, esta descrito como “hacia las [partes] siguientes” (“hacia la parte trasera” en mi traducción). No existe una versión satisfactoria de estos términos en el lenguaje moderno. Uno no puede utilizar los términos “Oeste” y “Este” dado que estos deben estar reservados para los términos que utiliza Ptolomeo de  y , que son confinados en situaciones donde el observador terrestre esta involucrado. Es una distorsión [gramatical] al traducirla (desde Manitius) “en orden inverso de los signos” y “en orden de los signos”, ya que implica que los términos definen coordenadas eclípticas estando expresadas en el sistema ecuatorial, y bien suele ser cierto que un objeto celeste  (“se dirija hacia adelante”) por sobre otro, tendrá una longitud eclíptica menor, si sus latitudes difieren bastante lo contrario puede ser válido, especialmente en latitudes eclípticas mayores. Precisamente esta situación ocurre en el catálogo de las estrellas, pese a la declaración de Ptolomeo en el Libro VII Capítulo 04, donde los términos en su catálogo definen las coordenadas eclípticas (ver allí en la nota de referencia nro. 7). Soy consciente también, que mi elección tiene demasiados inconvenientes, por lo que he tenido que asentarlo como “hacia adelante” para , y “hacia la parte trasera” para . Esto siempre implica “con respecto al movimiento diario de Este a Oeste”, con la paradójica consecuencia, como remarque arriba, que un objeto ubicado en la eclíptica "hacia adelante” (Oeste) respecto de otro, tiene una longitud menor. De cualquier modo, he cometido una inconsistencia al traducir el nombre derivado de  como “retrógrado”. Es utilizado solo para el segmento de los cursos de los cinco planetas que revierten su dirección de movimiento, lo cuál podría ser demasiado confuso de explicar como “movimiento hacia adelante”.

Eclíptica. Ptolomeo nunca se refiere a este círculo con el término  (que estrictamente deriva su significado como “en donde suceden los eclipses”). Su término normal es , que significa “el (círculo) a lo largo por el medio de los signos zodiacales” (por ej. HI 16,23-4); más enteramente, , “el círculo inclinado a lo largo por el medio de los signos zodiacales” (HI 64,4). Ocasionalmente, cuando el contexto es claro, simplemente , “círculo inclinado” (HI 8,22). Sin embargo, más tarde puede ser utilizado para otras cosas, tal como para la órbita de la Luna (que esta “inclinada” sobre la eclíptica). Normalmente uso la palabra “eclíptica” en toda la traducción.

Signo [zodiacal]. La subdivisión convencional de la eclíptica dentro de los doce treinta grados (30º) que se extienden a lo largo, son llamados Aries, Taurus, etc. Para ello Ptolomeo no utiliza el término  (“el signo animal”), sino  (“doce”), probablemente porque desea distinguir a la eclíptica, como un círculo imaginario en la zona del Zodíaco, siendo la presente banda de constelaciones.

Estrella: el término griego  realmente significa “cuerpo celestial”, y puede ser utilizado indiferentemente para una estrella (en el sentido moderno), un planeta, o aún para el Sol y la Luna. Cuando Ptolomeo desea distinguir lo que nosotros llamamos estrellas, él dice “estrellas fijas”. Normalmente lo traduzco  de acuerdo al contexto, como “planeta”, “estrella” o “cuerpo”. No obstante, en el Libro I Capítulos 03-08, donde Ptolomeo utiliza el término para incluir todo cuerpo celestial, también utilicé la palabra “estrella” en ese sentido (literal). Cuando se nombran los cinco planetas, Ptolomeo también, siempre usa la frase “estrella de...”, entonces  (), “(estrella) de Kronos”. Simplemente la traduzco siempre como “Saturno”, etc.

Latitud (celestial):  (literalmente “anchura”) no solo se refiere a “la dirección ortogonal hacia la eclíptica”, sino a cualquier dirección “vertical”, por ej. aquella normal al Ecuador. En tales casos no utilizo “latitud”, sino otro término apropiado (ver Libro I Capítulo 12 nota de referencia nro. 6). Sin embargo, en el Libro VII Capítulo 03, fui forzado en utilizar [el término] “latitud” para expresar los bastos significados generales del griego (ver Libro VII Capítulo 03 nota de referencia nro. 2).

Ptolomeo utiliza , tanto como adjetivo o nombre. Este término puede ser, y en último caso, que uno siempre tenga que entenderlo como , “círculo excéntrico”. De cualquier modo, para evitar ambigüedades, he denotado consistentemente (y siguiendo el uso medieval) el nombre de “excéntrica” y el adjetivo “excéntrico”. Una “excéntrica” es simplemente un círculo excéntrico. Similarmente “concéntrica” y “concéntrico”.

Ocasionalmente he utilizado el término medieval equivalente de “deferente” para denotar el círculo sobre el cuál un epiciclo es “transportado”. Ptolomeo no tiene una palabra equivalente, pero he utilizado frases tales como “la concéntrica transporta el epiciclo”, “el círculo transportándolo”.

Anomalía: como se observa en el ejemplo de Pedersen (139 en n.9), , en el Almagesto tiene un número de significados diferentes. No obstante dada la ambigüedad, generalmente he suministrado  y el adjetivo desde el cuál es derivado, , por “anomalía”, “anomalístico”, necesariamente también más tarde, lo he tenido que traducir literalmente como “no uniforme”. Ya refiriéndose al movimiento “no uniforme”, “anomalía” es también utilizado para el movimiento medio (en consecuencia “uniforme”) de la Luna y de los planetas sobre sus epiciclos (porque el movimiento en un epiciclo produce la apariencia de “no uniformidad”). Para los planetas Ptolomeo distingue entre “anomalía sinódica” (, “la anomalía con respecto al Sol”, HII 255,8), que produce el fenómeno retrógrado y varía con la elongación del planeta desde el Sol, y la “anomalía eclíptica” (, HII 258,11), que varía de acuerdo a la posición del planeta en la eclíptica.

Ecuación: utilicé convenientemente este término medieval para el ángulo o arco a ser aplicado al movimiento medio para “corregirlo”, teniéndolo en cuenta en un aspecto particular del modelo geométrico. Ptolomeo utiliza los términos imprecisos de  “diferencia” (también utilizado en muchas otras cosas) y  (“cantidad a ser sumada o sustraída”). La “Ecuación de la Anomalía” se refiere a la corrección para la posición variable de un cuerpo en su epiciclo, y la “Ecuación del Centro” (solo en los pies de página, no en el texto) a la corrección debida a la excentricidad de la deferente del planeta.

Centrum: ocasionalmente he utilizado este término medieval en los pies de página para denotar la distancia angular desde el apogeo (ver mas abajo) al centro del epiciclo.

Elongación: () es la distancia angular a lo largo de la eclíptica entre dos objetos o puntos. Es utilizado en forma particular, pero no exclusivamente, para la distancia eclíptica entre el Sol y la Luna.

Apogeo y Perigeo: son simplemente las transcripciones de  y , literalmente, “el [punto] lejos de la Tierra” y “[punto] cerca de la Tierra”. Estos son los términos usuales de los puntos que tiene un cuerpo sobre la órbita del mismo, estando lo más lejos y lo más cerca del observador terrestre. Ptolomeo usa también las formas superlativas  () , (“punto más lejos (más cerca) de la Tierra”), sin ninguna diferencia obvia en su significado. De cualquier modo, en el caso de Mercurio, la traducción de ambas por “perigeo” genera una ambigüedad. Para todos los otros cuerpos, en los modelos de Ptolomeo, el perigeo es diametralmente opuesto al apogeo, pero para Mercurio el punto de mayor aproximación es de unos 120º desde el apogeo. Ptolomeo aún se refiere al punto 180º desde el apogeo como desde el “perigeo” () de Mercurio, y cuando desea referirse al punto de mayor aproximación del planeta utiliza el superlativo (). He mitigado esta ambigüedad traduciéndolo más tarde, no como “perigeo”, sino como “más cercano a la Tierra” (solamente para Mercurio).

Fase: utilizado para las estrellas fijas y los planetas, es simplemente una transcripción de , y es un término general incluyendo todas las “configuraciones con respecto al Sol” (listado por Ptolomeo en el Libro VIII Capítulo 04, y ejemplificado en su trabajo parcial existente , “fases de las estrellas fijas”), tal como la primera visibilidad en la puesta, o la última visibilidad justamente antes del crepúsculo matutino. Pero el significado literal de  es “apariencia”, y Ptolomeo también lo utiliza para dar específicamente el significado de “primera visibilidad” de un cuerpo después de un período de invisibilidad. Para prevenir ambigüedades, lo he traducido posteriormente en el caso de “primera visibilidad”, reservando [la palabra] “fase” para el término general.

(iv) Refiriéndose al Sol y a la Luna:

Conjunción: es un término válido suministrado desde  (“encuentro”), en tanto “oposición”  (literalmente “Luna llena”, que ocurre cuando el Sol y la Luna están en oposición). Sizigias: es la mejor traducción de  (literalmente “juntos”), un término general para denotar tanto una como ambas, conjunciones y oposiciones. En los eclipses las fases parciales son denotadas por “inmersión” (, “entrando en”, la fase desde el principio del eclipse hacia la totalidad) y “emersión” (, “llenándola nuevamente [de luz]”, la fase desde el fin de la totalidad hacia el fin del eclipse). La fase total es denotada como  (“restante o remanente”) y suministrada por la “duración (de la totalidad)” [30].

(v) Recuento del Tiempo:

Ptolomeo frecuentemente utiliza el término , que combina las palabras griegas para la noche y el día, significando al “día solar” de 24 horas. En español este no es un término tan conveniente. Generalmente lo traduzco “día” cuando ninguna ambigüedad sea posible, aunque ocasionalmente tiene que ser escrita como una frase consistente (por ej. en el Libro II Capítulo 03 = HI 96, 7-9).

Desde que usamos relojes, conocemos el tiempo por “el día solar medio” de longitud uniforme, siendo el promedio de tiempo que toma el Sol de ir desde un meridiano hasta el (mismo) siguiente. En la antigüedad, donde el significado normal de tiempo “versado” era el del reloj de Sol, usualmente este era tomado en cuenta como “el día solar verdadero”, de longitud variable, tiempo tomado por el Sol en ir desde un meridiano hasta el próximo en un día específico. En el Libro III Capítulo 10 Ptolomeo explica porque estos son diferentes, y como se modifica uno con el otro. Utiliza los términos  (“días uniformes”) y  (“días no uniformes”) para los días solares medios y verdaderos respectivamente. Cuando habla acerca de los intervalos, frecuentemente se refiere a aquellos medidos en días solares verdaderos como “recontados simplemente”, y aquellos medidos en días solares medios como “recontados con exactitud”.

El tipo de horas utilizadas normalmente en el mundo antiguo eran las “horas de estación” (), algunas veces conocidas como “horas civiles”. Una hora era la duodécima parte de la longitud del día solar o de la noche en un determinado lugar, entonces la longitud de una hora variaba de acuerdo a la latitud terrestre y la época del año, y un día-hora era de longitud diferente respecto de una noche-hora, excepto en los equinoccios. No obstante para propósitos astronómicos, la vigésima cuarta parte de un día era utilizada, esto fue conocido como “horas equinocciales” (), dado que ellas eran de la misma longitud como la hora en la estación del equinoccio. Si un número ordinal esta junto a una hora, esto indica una hora de estación, contada desde la salida del Sol (o la puesta, sí es especificada por “de noche” o por el contexto). Entonces “la hora sexta” es la misma que la del mediodía.

Grados de tiempo: otro camino de medir el tiempo fue el “valor del Ecuador celeste” que ha pasado un límite (el del horizonte o el del meridiano). Frecuentemente fue asociado con los tiempos de salida de los arcos eclípticos. Esta medición era [dada] en grados. De los 360º del Ecuador culminando en el meridiano cerca de un día, un “grado de tiempo” era igual a la decimoquinta parte de una hora equinoccial o 4 minutos. El término griego es  (“tiempo ecuatorial”), algunas veces abreviado como  (“tiempo”).

(vi) Otras consideraciones

Medio (): puede implicar “el promedio en longitud” (tal como en “el mes sinódico medio”) o “uniforme” (como en “movimiento medio en longitud”).

Hipótesis: he usado este término con cierta duda para traducir , donde también la connotación en el Almagesto nunca coincide realmente con la moderna. Por donde fuere, utilizamos el término “hipótesis” para denotar una teoría tentativa que aún tiene que ser verificada, Ptolomeo comúnmente da el significado de  algo más que “modelo”, “sistema de explicación”, varias veces verídico refiriéndose a “las hipótesis que hemos demostrado”. Esta palabra aún retiene mucho de su significado etimológico como “base sobre la cuál algo también es construido”. Las formas verbales correspondientes son , la que he traducido frecuentemente no solamente como “asume”, sino también como “esto es dado”. Siendo términos estándares de la geometría griega, en un sentido, como sucedieron en principio (inicialmente) con Euclides.

Procedimientos de la editorial

Dado que la traducción esta principalmente basada en el texto de Heiberg, este esta relacionado a la presente edición por medio de un agregado (no presente en esta traducción al español), en el margen, de los números de página de Heiberg. Aquí y en otras partes las referencias a Heiberg son precedidas por una “H”. Entonces HI 236,15 significa la “edición de Heiberg, Vol. I página 236 línea 15”. Donde el contexto lo hace innecesario, el número de volumen es omitido.

Los corchetes son utilizados de la siguiente forma. Los corchetes [ ] encierran adiciones explicativas o expansiones del texto griego del traductor. Las llaves { } encierran pasajes, los cuales creo, son posteriormente agregados al texto original de Ptolomeo. Los paréntesis ( ) son utilizados simplemente para clarificar, para expresar mejor el buen concepto (sintaxis) de la secuencia del autor.

Como se explicó al comienzo de la introducción, creo que la lista de los encabezados del capítulo que preceden cada libro fueron agregados posteriormente. No obstante, sirve como propósito de gran utilidad, su agrupado juntamente al principio de la obra para servir como tabla de contenidos.

No he realizado un esfuerzo de brindar un comentario contínuo, aunque doy al lector las secciones relevantes de la obra de Olaf Pedersen “Una revisión del Almagesto” (abreviado “Pedersen”) y la de O. Neugebauer “Historia de la Astronomía Matemática Antigua” (abreviado HAMA). Mis “pies de página” son confinados a los casos particulares no tratados por ellos, requiriendo alguna elaboración, y a las correcciones textuales. En Cálculos, sin embargo, para cada tipo de problemas he provisto ejemplos elaborados que surgen del Almagesto (incluyendo aquellos donde el uso de las tablas no fuera enteramente trivial), excepto donde Ptolomeo propiamente dicho da un ejemplo desarrollado. Donde fuera posible, mis ejemplos son tomados de cálculos u observaciones presentes, ocurridas en el Almagesto. El Apéndice B lista todas mis correcciones al texto de Heiberg (no presente en esta traducción al español). En Cálculos (Ejemplo 16) se discute el problema de derivación de los Movimientos Planetarios Medios de Ptolomeo, que nunca han sido tratados en forma adecuada.

El índice (no presente en esta traducción al español), incluye todos los nombres propios encontrados en el texto, y ciertos tópicos selectos (generalmente tomados de la introducción y en los pies de página). Este también contiene todas las observaciones registradas en el Almagesto, bajo el tópico o del objeto celeste concerniente (por ej. “equinoccio”, “Luna”). Para una lista de observaciones en orden cronológico el lector puede referirse al Apéndice A de Pedersen [o bien en la Tabla Cronológica de las Observaciones (traductor al español)].

En los diagramas dibujados, he tratado de reproducir la tradición del manuscrito, mientras al mismo tiempo, haciendo las figuras tan claras [como fuera posible], las hice por medio de un detalle de puntos sin ambigüedades, y me vi forzado hacer varios cambios, pero no las he “modernizado”. Donde una figura me pareció inadecuada, no la he cambiado, aunque si he adicionado una explicación correspondiente. Tales explicaciones (y otras suplementarias) de las figuras, son distinguidas por números alfabéticos (“Fig. A”, etc.), por donde quiera que estuvieran, las figuras reproducidas en el Almagesto son numeradas de acuerdo al libro y al orden dentro de ese libro (entonces “Fig. 3.10” indica que es el décimo diagrama en el Libro III, mientras que en los manuscritos usualmente estas no son numeradas, pero donde se hallen, son numeradas en forma separada en cada libro). He representado las letras griegas de las figuras según el siguiente sistema:

Tabla del Alfabeto griego
Tabla del Alfabeto griego

Otros símbolos convencionales y sus abreviaciones

Abreviatura Descripción
e Excentricidad
r Radio del epiciclo o del cuerpo
M Longitud del día más largo en horas
m Longitud del día más corto en horas
R Radio del círculo principal
α (1) Ascensión Recta

(2) Anomalía

β Latitud celeste
δ Declinación
ε Oblicuidad de la Eclíptica
η Elongación
θ Nutación
ι Inclinación de la órbita (de la Luna o del planeta)
κ “Centrum”, por ej. distancia desde el apogeo
λ Longitud
ρ (1) Ascensión Oblicua

(2) Distancia Geocéntrica

φ Latitud terrestre
ω Distancia desde el punto norte sobre la órbita

Una barra sobre una letra denota “medio/a”, una sobre seg. λ sería “Longitud Media”.

Las siguientes notaciones son utilizadas como exponentes (por ej. 2^p), para denotar unidades:

Unidad Descripción
d Días
h Horas Equinocciales
m Meses
a Años
p “partes”, por ej. las unidades arbitrarias en cálculos trigonométricos (ver mas arriba en (c) Trigonometría)
º Grados
ºº Semi Grados (por ej. 2ºº = 1º, ver mas arriba en (c) Trigonometría)
º/d Grados por Día

En el catálogo de estrellas un * indica solamente cierta duda acerca de la lectura. Ver en el Libro VII Capítulo 5, nota de referencia nro. 95, para otras abreviaturas en particular del catálogo de estrellas.

Signos Zodiacales
Símbolo Zodíaco en Longitud
♈︎ Aries 0º = 0º
♉︎ Taurus 0º = 30º
♊︎ Gemini 0º = 60º
♋︎ Cancer 0º = 90º
♌︎ Leo 0º = 120º
♍︎ Virgo 0º = 150º
♎︎ Libra 0º = 180º
♏︎ Scorpius 0º = 210º
♐︎ Sagittarius 0º = 240º
♑︎ Capricornus 0º = 270º
♒︎ Aquarius 0º = 300º
♓︎ Pisces 0º = 330º
Símbolos Planetarios
Símbolo Objeto Celeste
♄ Saturno
♃ Júpiter
♂ Marte
♀ Venus
☿ Mercurio
☉ Sol
☽︎ Luna
Otros Símbolos Astronómicos
Símbolo Objeto Celeste
🜨 Tierra
☊ Nodo ascendente
☋ Nodo descendente

En las representaciones “sexagesimales” tales como: 6,13;10,0,58 ver explicaciones mas arriba en (c) Trigonometría.

Para los símbolos matemáticos || y ≡ (cuyos significados: “son similares a”) y (“es congruente a”), ver explicaciones mas arriba en (f) Explicación de términos especiales.

Para “M.T.I.” y “M.T.II.”, ver explicaciones mas arriba en (f) Explicación de términos especiales.

Para las abreviaciones en el manuscrito, ver explicaciones mas arriba en La Traducción.

Ir al Prefacio Contenidos Ir al Libro I - Capítulo 1

Notas de referencia

  1. ↑ Por ej. Galeno, “Niños en el Séptimo Mes”, ed. Walzer 347, 350; comentarios en la obra de Hipócrates “Aires, Aguas y Lugares”, (ver GAS VI 98). Vettius Valens, “Antología”, 354.
  2. ↑ La evidencia en la práctica astronómica en la III centuria desgraciadamente es menor, pero existe un fragmento de un texto cerca del 213 d. C. el cual describe muy de cerca el Almagesto (ver HAMA II 948-49), y existen varios papiros de esa centuria comentando las Tablas Manuales (Ibíd. 974-75,979-80). El Papiro Rylans 27 (c. 260) hace mención al solsticio de Ptolomeo y a observaciones del equinoccio en el Libro III Capítulo 2 del Almagesto, y a finales de la III centuria Porfirio (“Comentarios sobre [la Teoría] Armónica [de Ptolomeo]” 2, p. 24, 15ff.) hace mención al Almagesto en el Libro I Capítulo 2 (H9, 11-16). La única evidencia que he visto del Almagesto en la II centuria, esta en Galen, en los comentarios sobre Hipócrates en "Aires, Aguas y Lugares" III (Cairo, Tal’at tibb 550, p. 73a), donde Ptolomeo es mencionado al final de una lista de autoridades en astronomía, siendo seguramente una interpolación de la tradición Árabe, ya que Ptolomeo es caracterizado como “el rey de Egipto”.
  3. ↑ Sé que esto no es satisfactorio. Doy un muy breve bosquejo, Toomer [5] 202.
  4. ↑ Ver Kunitzsch, Der Almagest, para una completa reseña, especialmente en 15-71. Kunitzsch también ha publicado el trabajo de ibn as-Salah (ver la Bibliografía).
    Primeros traductores del Almagesto en tiempos del Islam
    Astrónomo Lugar Nacimiento Ciudad Traducción Califato Año Traducción Alfabeto Origen-Traducido
    Sahl ibn Bishr al-Israili o Rabban al-Tabari (Zahel) Tabaristán - (c. 786-845?) Tabaristán Abasí 820? Griego al Árabe
    Al-Ḥajjāj ibn Yūsuf ibn Maṭar ? - (786-833) Bagdad Abasí 829 Griego al Árabe
    Abū Yaʿqūb Isḥāq ibn Ḥunayn Bagdad - (830-910) Bagdad Abasí 830? Griego al Árabe
    Thābit ibn Qurra ibn Marwán al-Sabi al-Harrani Harrán - (826-901) Bagdad Abasí 890? Griego al Árabe
    Abd al-Rahman al-Sufi Rayy - (903-986) Isfahán Dinastía Búyida 960-970? Griego al Árabe

    Tabla según el traductor al español.

  5. ↑ Ver Haskins, “Estudios”, 103-112,157-165.
    Nota del traductor al español:
    En el siglo XII Palermo, Sicilia, tuvo una principal ventaja sobre su ubicación geográfica con respecto a Toledo, y más por haber sido parte de la Magna Grecia, por lo tanto más influenciada aún por la cultura de la antigua Grecia y relacionada con las copias griegas traducidas al latín realizadas en el lugar, caso diferente al de la Escuela de Traductores de Toledo traducidas del árabe al latín, también en el siglo XII.
    En esa gran isla los altos oficiales sabían más de una lengua dado el lugar, ruta marítima hacia Europa. Las traducciones al latín realizadas en Palermo eran muy requeridas por los estudiantes de la península itálica llevando a su regreso varios volúmenes ya traducidos a ese idioma, y también hacia otras zonas transalpinas.
    El Almagesto, fue obra importante en la Edad Media y la más importante en astronomía entre los sarracenos (islámicos), aunque la mayor difusión del mismo en Europa (Occidente Europeo) fue por parte del traductor del árabe al latín Gerardo de Cremona (Toledo, finalizada en el año 1175).
    El prólogo del manuscrito Vat. Lat. 2056 de la Biblioteca Apostólica Vaticana corresponde a una copia en latín de la traducción siciliana del año 1160, perteneciente a Coluccio Salutati y de finales del Siglo XIII o principios del Siglo XIV.
    Tal prólogo detalla que la traducción fue dedicada a un profesor de matemáticas, traducida del griego al latín por un estudiante de medicina de la Escuela Médica Salernitana (Salerno) y realizada en Palermo aproximadamente el año 1160.
    El estudiante describe que la copia griega del Almagesto fue traída desde Constantinopla regalo de los “tesoros” del emperador bizantino Manuel Komneno al rey Guillermo I de Sicilia y traída desde allí en el año 1158 por el embajador del reino siciliano, Enrico Aristippo, conocedor del griego y del latín, siendo arconte (gobernador) de Catania desde 1156.
    Esta copia griega le fue entregada al estudiante de medicina cuando Aristippo estaba observando el monte Etna y encontrándose con él en la laguna cerca de la ciudad de Pergusa a comienzos del año 1160, mismo año que empezó el estudiante con su traducción y terminándola 3 o 4 años más tarde, bastante antes de la realizada por Gerardo de Cremona finalizada en el año 1175 en Toledo. Esta traducción fue superior a la de Cremona, hecha con razonable inteligencia, dado que el estudiante conocía el griego y su lengua de origen el latín, traduciendo palabra por palabra, contrario a Cremona que tuvo que consultar a un intérprete del árabe al latín. La traducción siciliana, entonces, es afín y muy próxima al Códex A, de Heiberg, el mejor manuscrito griego entre todos los actuales. Tal traducción siciliana se encuentra probablemente en la Biblioteca Marciana de Venezia.
    La corte de Guillermo I contó con dos traductores principales, los funcionarios Aristippo y Hugo Falcandus (pseudónimo de Eugenio de Palermo), este último miembro de la curia y probablemente notario desde 1154 hasta 1169. Relató en su obra “Historia de los tiranos de Sicilia” todo lo acontecido en tal corte escribiendo “me ocupo sobre todo de lo que sucede en la corte” y ayudó a traducir el Almagesto a Aristipo comentando que Eugenio el Emir “conocía muy bien el griego y el árabe y no ignoraba el latín”.
    • Este último párrafo es según el libro “El Renacimiento del Siglo XII” de Charles Homer Haskins. Traducción al español de Claudia Casanova (2013). Ed. Ático de los Libros.
  6. ↑ Kunitzsch, “Der Almagest”, 83-112, sobre esto da una valorable descripción de la evidencia, y en el método de trabajo de Gerardo de Cremona: evidentemente este utilizó más de una de las traducciones al árabe.
  7. ↑ He tenido reconocimiento en todos aquellos casos donde mis correcciones han sido anticipadas por otros, a saber por Manitius.
  8. ↑ Ver la nota en Roma [1] I, y cotéjese (con Teón de Alejandría) II n. (1).
  9. ↑ Para mayores detalles ver HAMA II 755-71.
  10. ↑ Ptolomeo conoce el equivalente de la fórmula del seno, nombrada de tal manera que en el triángulo general, los lados son proporcionales a las cuerdas de dos de los ángulos opuestos, pero asombrosamente lo utiliza en pocos lugares. Por ej. allí en el Libro IX Capítulo 10 (cf. nota de referencia nro. 7) .
  11. ↑ A lo largo de este libro uso el sistema “astronómico” de fechas acorde a la era Cristiana, dado que es mucho más simplificado en el cálculo de intervalos respecto al sistema “a. C. / d. C.”. En este último caso, el año –1 corresponde al 2 a. C., el año 0 al 1 a. C., el año 1 al 1 d. C., etc.
    Nota del traductor al español: en las notas de referencias, donde he insertado tablas con datos acerca de las observaciones de los astrónomos, he utilizado el recuento de años referido a los ejes cartesianos donde el punto 0 (cero), en el eje de las X (abscisas), es el comienzo de la era cristiana y de la era antes de Cristo. Es decir el 1° de Enero del año 1 d.C. a las 00:00 hs., es el punto inicial (origen de las coordenadas) en el recuento del tiempo.
    Por ejemplo: el año 1 d.C. es el +1, el año anterior a este es el 1 a.C. siendo el -1 en mi recuento, el 2 a.C. es el -2, y así sucesivamente. En el Libro III Capítulo 2 el Equinoccio de Otoño Toomer lo expresa como el [27 de Septiembre del -161] siendo el 27 de Septiembre del 162 a.C. según su recuento. En el sistema que he adoptado esta última fecha es el -162 que lo expreso entre paréntesis (-162).
  12. ↑ Fragmentos de papiros de estos reyes listados se encuentran en los papiros de Oxirrinco. 1.35 y Sattler, “Studien” 39-50. Estos son, no obstante, posteriores a Ptolomeo. P. Oxy, 19.2222, una lista de los Ptolomeos de Egipto, es más temprana que la del Almagesto, pero en formato es muy diferente al listado de los reyes de Ptolomeo.
  13. ↑ Este no es conocido, ya que estos dos reyes están “combinados”. En las tablas cuneiformes (por ej. la lista de reyes traducida en Pritchard, “Ancient Near Easter Texts” 272 (iv), ellos aparecen consecutivamente, Ukin-zer siendo asignada 3 años y Pulu 2.
  14. ↑ Esta debe ser una forma corrupta en la tradición griega de Arses (‘A), la forma usual de los nombres de los reyes (también conocida como ‘O).
  15. ↑ Fue estudiado y revisado hace mucho tiempo atrás. Ver Usener, MGH XIII.3 p. 441, con referencias a la literatura griega en su n.5.
  16. ↑ En las tablas manuales Ptolomeo adoptó la “era de Filipo” (que ya ocurre en el Almagesto como por ej. con la “muerte de Alejandro”); por lo tanto en el manuscrito, los totales de la era de Nabonassar, van hasta Alejandro el Macedonio (no. 31), y un nuevo sistema de totales comienza con Filipo (no. 32). He convertido todos estos últimos totales a la era de Nabonassar por medio de la adición de 424 [años] en cada uno de ellos. Cf. Schram p. 173.
  17. ↑ Para una discusión en detalle ver Toomer [7]. Allí doy los argumentos suponiendo que el propósito de Metón no fue el de reformar el calendario ateniense, sino de establecer una “cronología astronómica”.
  18. ↑ Son las fechas de los tres eclipses en el Libro IV Capítulo 11, a través de lo observado en Babilonia, y están dadas acorde al Arconte ateniense y al mes ateniense; probablemente son del calendario Metónico.
  19. ↑ Aquellos que deseen ser puntillosos en los detalles y en la literatura, consultar Ginzel II 409-19 y Alan E. Samuel, “Greek and Roman Chronology”, 42-9.
  20. ↑ Por este sistema ver Alan Edouard Samuel, “Greek and Roman Chronology” 59-60. No sé porqué no es utilizado en las otras tres fechas Calípicas en las que los días son numerados consecutivamente.
  21. ↑ Esto esta listado convenientemente en Parker-Dubberstein.
  22. ↑ Para detalles ver Alan E. Samuel, “Greek and Roman Chronology”, 140-2. Sin embargo, Alan E. Samuel esta errado en decir que el Almagesto brinda la evidencia de que la asimilación ocurrió tan tempranamente como el fechado de la observación más antigua (temprana) (Noviembre de –244). En los registros cuneiformes desde los cuales fueron derivados los nombres babilonios, estos últimos deben haber sido utilizados. Solamente esto sucedió cuando fueron traducidos al griego (que pudo haber ocurrido una centuria más tarde) donde los nombres macedonios fueron sustituidos.
  23. ↑ El lector interesado puede consultar: HAMA III 1067 n.2 y Alan E. Samuel, “Greek and Roman Chronology” 50, n.6.
  24. ↑ La falta de un asterisco no implica que yo considere la lectura adoptada de Ptolomeo más allá de cualquier cuestión, sino que no he tenido solo una buena razón para hacerlo.
  25. ↑ Ver la crítica de Kunitzsch, “Der Almagest” 46.
  26. ↑ Nota del traductor al español: Agregué un link en la "Designación Moderna" y la columna "Nombre Actual" para cada estrella.
  27. ↑ El trabajo de Thiele, “Antike Himmelsbilder”, es de poca ayuda, aunque me he referido también a ella para ilustrar algunos detalles.
  28. ↑ Cf. texto difícil de entender el de Arato, Maass, “Comm. in Arat. p. 384 no. 251”: “los signos vistos desde dentro con respecto a los cielos... aunque ellos tienen sus espaldas hacia el globo, entonces sus caras pueden ser vistas. Por consiguiente, si él dice “a mano derecha” o “a mano izquierda” y lo encontramos opuestos en el globo, no debemos confundirnos”.
  29. ↑ Notablemente, donde Ptolomeo describe una estrella como una “masa nebulosa” (), prefiero dar el término Cúmulo Globular (abreviado “CGlo”) o Cumulo Galáctico (abreviado “CGal”) para alguna estrella en particular dentro de ella.
  30. ↑ Dígitos, Magnitudes y Porcentaje de Sombreado en Eclipses Lunares. Dígitos, forma de medir la magnitud del eclipse en tiempos de Claudio Ptolomeo. El cálculo de los dígitos es la fracción sombreada o eclipsada del diámetro lunar siendo igual a la Magnitud actual -menor o igual a 1- multiplicada por 12 dígitos (100% eclipsada). Ver Dígitos y Magnitudes en Eclipses Lunares.
Obtenido de «https://es.wikisource.org/w/index.php?title=Almagesto:_Introducción&oldid=1453184»