Almagesto: Libro X - Capítulo 08
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
{Demostración del tamaño del Epiciclo de Marte}
Nuestra siguiente tarea es demostrar la proporción (razón) del tamaño del epiciclo [de Marte]. Para tal propósito tomamos una observación que obtuvimos de la observación [realizada] (con el Astrolabio) alrededor de 3 días después de la tercera oposición, esto es, en el segundo año de Antonino Pío, 15/16 de Epiphi [XI] en el calendario Egipcio [30/31 de Mayo de 139], 3 horas equinocciales antes de la medianoche [2]. [Esta fue la hora,] dado que el vigésimo grado de Libra (por ej. ♎︎ 19º - 20º) estuvo culminando de acuerdo con el astrolabio, mientras la [posición media del] Sol estuvo en ♊︎ 5;27º [también] en ese momento. Ahora, cuando la estrella en la espiga de trigo (Spica) fue observada [en el instrumento] en su propia posición, Marte fue observado tener una longitud de ♐︎ 1 ⅗º. En ese mismo instante este fue observado estar a la misma distancia (1 ⅗º) hacia atrás del centro de la Luna [2]. Ahora, en aquel instante, la posición de la Luna fue la siguiente [3]:
| longitud media | ♐︎ 4;20º |
| longitud verdadera | ♏︎ 29;20º (ya que su distancia en anomalía desde el apogeo del epiciclo fue de 92º) |
| longitud aparente | ♐︎ 0º [4] |
Entonces, también desde estas consideraciones, la longitud de Marte fue de ♐︎ 1;36º, de acuerdo con la observación [con el astrolabio].
Por consiguiente, claramente, este estuvo a 53;54º por adelante del perigeo [5].
Y el intervalo entre la tercera oposición y esta observación comprende
| en longitud | alrededor de 1;32º |
| en anomalía | alrededor de 1;21º [6] |
Si sumamos esto último a las posiciones [medias] en la oposición en cuestión [7] demostrada anteriormente, tomamos, para el momento de esta observación;
| la distancia en longitud de Marte desde el apogeo de la Excéntrica: | 137;11º |
| la distancia en anomalía desde el apogeo del epiciclo: | 172;46º |
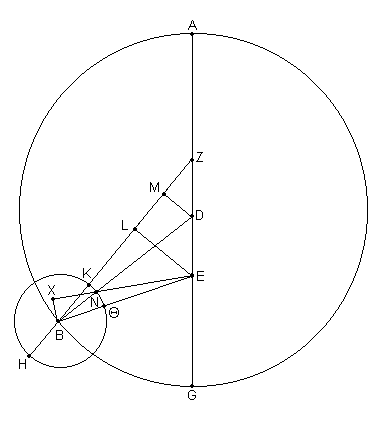
Con estos elementos como datos, sea ABG [Fig. 10.17] el círculo de la excéntrica con centro en D transportando el centro del epiciclo y el diámetro ADG, sobre el cual el centro de la eclíptica es tomado en E, y en Z el punto de la máxima excentricidad (por ej. de la Ecuante). Dibujar el epiciclo HΘK con centro en B, dibujar ZKBH, EΘB y DB, y eliminar las perpendiculares EL y DM desde los puntos D y E hasta ZB. Sea el planeta ubicado en el punto N del epiciclo, unir EN, BN, y eliminar la perpendicular BX desde B hasta EN prolongado.
Entonces, dado que la distancia del planeta desde el apogeo de la excéntrica es de 137;11º,
el ^ BZG = [180º - 137;11º =] 42;49º donde 4 ángulos rectos = 360º
el ^ BZG = [180º - 137;11º =] 85;38ºº donde 2 ángulos rectos = 360ºº.
Por lo tanto, en el círculo alrededor del triángulo rectángulo DZM,
arco DM = 85;38º
y arco ZM = 94;22º (suplementario).
Por consiguiente los arcos correspondientes
DM = 81;34p donde la hipotenusa DZ = 120p
y ZM = 88;1p donde la hipotenusa DZ = 120p.
Por lo tanto donde la distancia entre los centros, DZ = 6p,
y el radio de la excéntrica, DB = 60p,
DM = 4;5p
y ZM = 4;24p.
Y dado que DB² - DM² = BM²,
BM = 59;52p en las mismas unidades.
Similarmente, dado que ZM = ML, y EL = 2 * DM,
por sustracción, BL = 55;28p y EL = 8;10p en las mismas unidades.
Por consiguiente la hipotenusa [del triángulo rectángulo EBL] EB = 56;4p.
Por lo tanto, donde EB = 120p, EL = 17;28p,
y, en el círculo alrededor del triángulo rectángulo BEL,
arco EL = 16;44º
en consecuencia ^ ZBE = 16;44ºº donde 2 ángulos rectos = 360ºº.
Además, la distancia aparente del planeta Marte hacia delante del perigeo G,
el ^ GEX esta dado como de 53;54º donde 4 ángulos rectos = 360º
el ^ GEX esta dado como de 107;48º donde 2 ángulos rectos = 360ºº.
Y, en las mismas unidades, el ^ ZBE = 16;44ºº (demostrado anteriormente),
y el ^ GZB = 85;38ºº (dado),
entonces el ^ GEB = ^ ZBE + ^ GZB = 102;22ºº.
Por lo tanto, por sustracción [del ^ GEB desde el ^ GEX],
el ^ BEX = 5;26ºº en las mismas unidades,
y, en el círculo alrededor del triángulo rectángulo BEX
arco BX = 5;26º.
Entonces BX = 5;41p donde la hipotenusa EB = 120p.
Por lo tanto donde EB, como fue demostrado, = 56;4p,
y el radio de la excéntrica es de 60p,
BX = 2;39p.
Similarmente, dado que la distancia del punto N desde H el apogeo del epiciclo, fue de 172;46º, y [por lo tanto], desde el perigeo K, 7;14º,
el ^ KBN = 7;14º donde 4 ángulos rectos = 360º
el ^ KBN = 14;28ºº donde 2 ángulos rectos = 360ºº.
Pero el ^ KBΘ fue encontrado como de 16;44ºº en las mismas unidades.
Por lo tanto, por sustracción, el ^ NBΘ = 2;16ºº,
y, por adición, [del ^ NBΘ al ^ BEX], ^ XNB = 7;42ºº.
Por lo tanto, en el circulo alrededor del triángulo rectángulo BNX,
arco XB = 7;42º
y BX = 8;3p donde la hipotenusa BN = 120p.
Por lo tanto donde BX = 2;39p y el radio de la excéntrica = 60p,
el radio del epiciclo BN ≈ 39;30p.
Por lo tanto la proporción del radio de la excéntrica [dividido] el radio del epiciclo es 60 / 39;30.
Lo que se ha requerido para examinar.
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Libro X |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 |
Notas de referencia
- ↑ Sobre el método empleado aquí ver HAMA 179-80, y en Pedersen 283-6.
- ↑ 2,0 2,1 Fecha y horas calculadas con un programa de computación desde la observación realizada por Ptolomeo (actual Alejandría) de la siguiente:
Oposición de Marte en el día de la observación de Ptolomeo Fecha Hora Longitud del Sol Longitud de Marte Latitud de Marte Elongación Altura Azimut Magnitud Marte en Carta 30 de Mayo de 139 d. C. (139) 21:00 hs. ♊︎ 66° 42' 42" ♐︎ 242° 11' 27" -03° 12' 00" E 174° 28' 17" 24° 01' 49" 322° 06' 27" -2,5 Sagittarius 
Almagesto Observación 30.05.139 d. C. En ese instante, Marte se encontraba a: 4° 48' 30" (NNW) de Gama Sagittarius (Al Nasl, “la punta de la flecha”), a 07° 04' 48" (WNW) de Delta Sagittarius (Kaus Meridionalis, "la del centro del Arco") y a 08° 15' 55" (W) de Lambda Sagittarius (Kaus Borealis, "la parte Norte del arco").
Conjunción Luna-Marte en el instante de la observación de Ptolomeo (30.05.139 a las 21:00 hs.) Longitud Lunar Latitud Lunar Altura Azimut Fase - Fracción Iluminada Distancia Luna-Marte (centro a centro) Luna en Carta ♐︎ 240° 41' 14" +03° 54' 15" 29° 04' 317° 19' Llena - 100 % 6° 37' 12" (S) Sagittarius Almagesto Observación 30.05.139 d. C. La oposición de Marte ocurrió el 27 de Mayo de 139 d. C. (139) a las 07:20:23 hora local. Ese mismo día pasaba por el meridiano del lugar a las 23:46:46 hs., altura: 34° 50' y azimut: 0°. Distancia Tierra-Marte: 63.549.047,05 kms.
Nota del traductor al español: cartas y datos elaborados con mi software de aplicación "M1 Sistema Astronómico"©.
- ↑ Estas posiciones son calculadas (precisamente), no para las 21:00 hs., sino para las 20:37 hs., por ej. Ptolomeo ha aplicado la Ecuación del Tiempo con respecto a la época de -23 minutos (este [valor] debería ser alrededor de -25 ½ minutos).
- ↑ Literalmente "al principio de Sagittarius".
- ↑ El cual estuvo en ♑︎ 25;30º (final del Libro X Capítulo 7).
- ↑ Estos movimientos medios también están de acuerdo con un intervalo de 2 días 22 horas 37 minutos con respecto al intervalo de 2 días 23 horas (ver más arriba nota de referencia nro. 3).
- ↑ Leer (en el manuscrito D) en cambio de ' ("en la tercera oposición, que es la única en cuestión") en H348,9-10.
