Almagesto: Libro XIII - Capítulo 04
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
{Construcción de las tablas para las Posiciones Individuales en Latitud}
De lo anterior, luego, hemos establecido las cantidades generalmente aplicables a las máximas inclinaciones de las Excéntricas y de los Epiciclos. Pero con el fin de que seamos capaces de encontrar convenientemente y sistemáticamente las posiciones en Latitud para un momento dado [y] para las distancias individuales [desde el apogeo], también construimos 5 tablas para los 5 planetas. Cada una contiene el mismo número de líneas como las Tablas de las Anomalías [por ej. de 45], y 5 columnas. Las 2 primeras de esas columnas comprenden los argumentos, en el mismo sentido como en aquellas [tablas de las anomalías]; la tercera columna contiene las distancias latitudinales desde la Eclíptica correspondientes a los grados en particular del [movimiento sobre el] epiciclo, bajo la asunción de la máxima inclinación - para Venus y Mercurio esta es la inclinación en los nodos de la excéntrica, y para los otros tres planetas (Saturno, Júpiter y Marte) la inclinación en el límite Norte de la excéntrica. Para esto último, la cuarta columna contendrá cantidades similares correspondientes a [la inclinación] en el límite Sur, y en el caso de esos 3 planetas la máxima desviación hacia el Norte y hacia el Sur de las excéntricas ha sido también incluida en el cálculo. El camino por el cual hemos determinado tales cantidades para Venus y Mercurio se basa nuevamente en un teorema sencillo [para ambos planetas] de la siguiente manera.
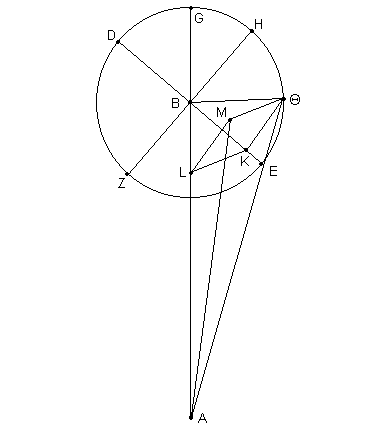
[Ver Fig. 13.2] En el plano ortogonal hasta la eclíptica, sea ABG la intersección de él con el plano de la eclíptica, y DBE la intersección [del plano eclíptico con] el plano del epiciclo. Sea A el centro de la eclíptica, B el centro del epiciclo, y AB la distancia del epiciclo en la máxima inclinación. Alrededor de B describir el epiciclo DZEH [1], y dibujar el diámetro ZBH perpendicular a DE. Sea el plano del epiciclo también tomado perpendicular al plano asumido [aquel plano ortogonal al plano de la eclíptica], así que cuando las líneas son dibujadas en él perpendiculares a DE, todas serán paralelas al plano de la eclíptica, exceptuando solamente a ZH, que se ubicará en el plano de la eclíptica.
Sea el problema entonces, dada la proporción de AB dividido BE, y la cantidad de la inclinación (por ej. del ^ ABE), encontrar las posiciones de los planetas en latitud cuando (como para tomar un ejemplo) ellos están a una distancia de 45º (donde [la circunferencia del] epiciclo es de 360º) desde E el perigeo del epiciclo. [Elegimos 45º] porque intentamos demostrar al mismo tiempo las diferencias en las posiciones en longitud producidas por esas [máximas] inclinaciones, y esas diferencias deberían alcanzar sus máximos por alrededor de la mitad del camino entre el perigeo E y las posiciones Z y H, dado que en esos puntos [las longitudes calculadas] son idénticas con las longitudes producidas sin considerar la inclinación.

Sea el arco EΘ cortado por la cantidad anterior (de arriba) de 45º, y eliminar ΘK perpendicular a BE, y KL, ΘM perpendicular al plano de la eclíptica. Unir ΘB, LM, AM y AΘ.
Inmediatamente es obvio que
[1] el cuadrilátero LKΘM tiene lados paralelos y ángulos rectos (dado que KΘ es paralelo al plano de la eclíptica); y
[2] la ecuación en longitud esta comprendida por el ^ LAM, y
[3] la posición en latitud esta comprendida por el ^ ΘAM (dado que los ángulos ALM y AMΘ se tornan también en ángulos rectos, porque la línea AM se ubica en el plano de la eclíptica) [2].
Demostración de las posiciones en latitud para Venus
Pero ahora debemos demostrar las cantidades numéricas de las posiciones requeridas a ser calculadas para cada uno de los planetas anteriores, y primero para Venus.
Dado que el arco EΘ = 45º donde [la circunferencia del] epiciclo es de 360º,
el ^ EBΘ (ya que este esta en el centro del epiciclo) = 45º donde 4 ángulos rectos = 360º
el ^ EBΘ (ya que este esta en el centro del epiciclo) = 90ºº donde 2 ángulos rectos = 360ºº.
Por lo tanto, en el círculo alrededor del triángulo rectángulo BΘK,
arco BK = arco KΘ = 90º.
Entonces las cuerdas correspondientes
BK = KΘ = 84;52p donde la hipotenusa BQ = 120p.
Por lo tanto donde BΘ, el radio del epiciclo, es de 43;10p,
y AB, la distancia media, es de 60p
(la máxima inclinación del epiciclo ocurre en aproximadamente este punto),
BK = KΘ = 0;32p.
Nuevamente, dado que el ángulo de inclinación,
el ^ ABE es tomado como 2;30º donde 4 ángulos rectos = 360º
el ^ ABE es tomado como 5ºº donde 2 ángulos rectos = 360ºº,
en el círculo alrededor del triángulo rectángulo BLK,
arco LK = 5º
y arco BL = 175º (suplementario).
Entonces las cuerdas correspondientes
KL = 5;14p donde la hipotenusa BK = 120p
y BL = 119;53p donde la hipotenusa BK = 120p.
Por lo tanto, donde la hipotenusa BK = 30;32p, y AB = 60p,
KL = 1;20p,
BL = 30;30p,
y, por sustracción [de BL desde AB], AL = 29;30p.
Pero, en las mismas unidades, LM = KΘ = 30;32p.
Por lo tanto la hipotenusa AM [= (AL² + LM²) ^ 0,5] = 42;57p en las mismas unidades.
Por lo tanto, donde la hipotenusa AM = 120p, LM = 86;19p,
y la ecuación en longitud en aquel punto,
el ^ LAM = 92;0ºº donde 2 ángulos rectos = 360ºº
el ^ LAM = 46;0º donde 4 ángulos rectos = 360º.
Similarmente, donde AM = 42;27p,
ΘM = KL = 1;20p;
y ΘM² + AM² = AΘ²,
entonces AΘ = 42;29p en las mismas unidades.
Por lo tanto, donde la hipotenusa AΘ = 120p,
ΘM = 3;46p,
y el ángulo de la desviación en latitud,
el ^ ΘAM = 3;36ºº donde 2 ángulos rectos = 360ºº
el ^ ΘAM = 1;48º donde 4 ángulos rectos = 360º.
Este [1;48º] es lo que pondremos en la tercera columna de la tabla de Venus sobre la línea conteniendo los '135º'.
Con el fin de hacer una comparación de la diferencia en la ecuación de la longitud que resulta [desde los cálculos de arriba], sea dibujada [Fig. 13.3] la figura correspondiente sin alguna inclinación del epiciclo. Entonces demostramos que

BK = KΘ = 30;32p donde AB = 60p,
entonces, por sustracción, AK = 29;28p;
y AK² + KΘ² = AΘ²,
entonces AΘ = 42;26p en las mismas unidades.
Por lo tanto, donde la hipotenusa AΘ = 120p, KΘ = 86;21p,
y el ángulo de la ecuación en longitud,
el ^ ΘAK = 92;3ºº donde 2 ángulos rectos = 360ºº
el ^ ΘAK = 46;2º, aproximadamente, donde 4 ángulos rectos = 360º.
Y con la inclinación este fue demostrado ser de 46º.
Por lo tanto la ecuación en longitud, calculada de acuerdo a la inclinación, fue menor a 2'.
Lo que se ha requerido para examinar [3].
Demostración de las posiciones en latitud para Mercurio
Nuevamente, también para permitirnos demostrar las posiciones [latitudinales] de Mercurio, sea dibujada una figura [Fig. 13.4] similar a la anterior, con el arco EΘ tomado como del mismo tamaño, 45º. Por consiguiente nuevamente
BK = KΘ = 84;52p donde la hipotenusa BΘ = 120p.
Por lo tanto, donde el radio del epiciclo, BΘ = 22;30p,
y AB, la distancia en [donde] ocurren las máximas inclinaciones, es de 56;40p (las cuáles las hemos demostrado previamente a todas) [4],
BK = KΘ = 15;55p en las mismas unidades.
Nuevamente, dado que por hipótesis el ángulo de la inclinación del epiciclo,
el ^ ABE = 6;15º donde 4 ángulos rectos = 360º
el ^ ABE = 12;30ºº donde 2 ángulos rectos = 360ºº,
en el círculo alrededor del triángulo rectángulo BKL,
arco LK = 12;30º
y arco BL = 167;30º (suplementario).
Entonces las cuerdas correspondientes
KL = 13;4p donde la hipotenusa BK = 120p
y BL = 119;17p donde la hipotenusa BK = 120p.
Por lo tanto donde BK, como demostramos, es de 15;55p,
y AB, por hipótesis, es de 56;40p,
KL = 1;44p,
BL = 15;49p,
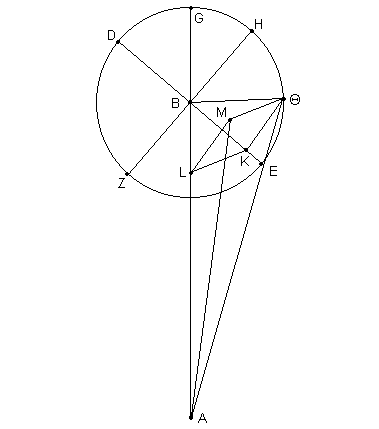
y, por sustracción [desde AB], AL = 40;51p en las mismas unidades.
Y LM = KΘ = 15;55p.
Y dado que AL² + LM² = AM²,
AM = 43;50p donde línea LM = 15;55p.
Por lo tanto, donde la hipotenusa AM = 120p, LM = 43;34p,
y el ángulo de la ecuación en longitud,
el ^ LAM = 42;34ºº donde 2 ángulos rectos = 360ºº
el ^ LAM = 21;17º donde 4 ángulos rectos = 360º.
Similarmente, donde AM = 43;50p,
ΘM = KL = 1;44p;
y AM² + ΘM² = AΘ²,
entonces AΘ = 43;52p en las mismas unidades.
Por lo tanto, donde la hipotenusa AΘ = 120p,
ΘM = 4;44p,
y el ángulo de la desviación en latitud,
el ^ ΘAM = 4;32ºº donde 2 ángulos rectos = 360ºº
el ^ ΘAM = 2;16º donde 4 ángulos rectos = 360º.
Estos [2;16º] es lo que nosotros entraremos en la tercera columna de la tabla para Mercurio sobre la misma línea, a saber, aquella conteniendo el argumento '135º'.
Con el fin nuevamente para hacer una comparación de la ecuación, sea allí dibujada la figura [Fig. 13.5] sin la inclinación [del epiciclo]. Luego demostramos que, donde la línea AB = 56;40p,
ΘK = KB = 15;55p,
y, por sustracción, obviamente, AK = 40;45p en las mismas unidades;
y AK² + KΘ² = AΘ²,
entonces AΘ = 43;45p donde ΘK = 15;55p.

Por lo tanto, donde la hipotenusa AΘ = 120p, ΘK = 43;39p,
y el ángulo de la ecuación en longitud,
el ^ KAΘ = 42;40ºº donde 2 ángulos rectos = 360ºº
el ^ KAΘ = 21;20º donde 4 ángulos rectos = 360º.
Pero demostramos que con la inclinación este estuvo en 21;17º.
Por lo tanto aquí también la ecuación en longitud calculada de acuerdo a la inclinación fue menor, de 3'.
Lo que se ha requerido para examinar.
Demostración de las posiciones en latitud para los otros 3 planetas: Saturno
Tal es, pues, el método por [medio] del cuál calculamos las posiciones en latitud en las máximas inclinaciones para esos dos planetas. Dado que las máximas inclinaciones ocurren cuando la excéntrica esta en el mismo plano como [el de] la eclíptica. Para los restantes 3 planetas, no obstante, calculamos [aquellas posiciones] por medio de un teorema que requiere un diagrama diferente, ya que [para ellos] las máximas inclinaciones del epiciclo ocurren cuando la inclinación de la excéntrica esta también en un máximo, y esto podría beneficiarnos para tener las posiciones en latitud resultantes desde ambas inclinaciones calculadas conjuntamente.
[Ver Fig. 13.6 y cf. Fig. T]. En el plano ortogonal a la eclíptica, nuevamente, sea AB la intersección de él con el plano de la eclíptica, AG la intersección del plano de la excéntrica, y DGE la intersección del plano del epiciclo. Sea A tomado como el centro de la eclíptica, y G como el centro del epiciclo, y sea DZEH el epiciclo descrito alrededor de G en tal sentido, nuevamente, que cuando las líneas son dibujadas perpendiculares a DE, el diámetro ZGH yace en el plano de la excéntrica y es paralelo al plano de la eclíptica, mientras las otras [perpendiculares] son paralelas a ambos planos anteriores (de arriba).

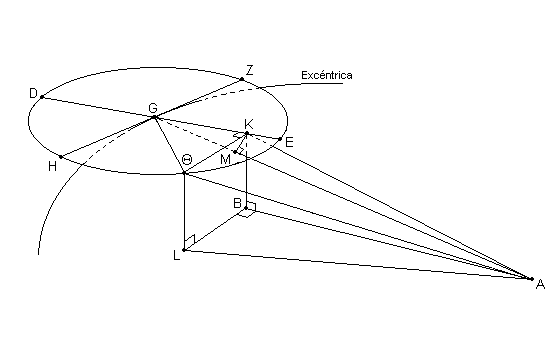
Similarmente, sea el arco EΘ cortado por la misma cantidad de 45º, y eliminar la perpendicular ΘK desde Θ (el punto en el cuál el planeta esta localizado), y también eliminar las perpendiculares ΘL, KB desde los puntos Θ y K al plano de la eclíptica. Unir BL y AL. Entonces, sea el problema de encontrar la ecuación en longitud, representada por el ^ BAL, y la posición en latitud, representada por el ^ LAΘ.
Entonces dibujar la perpendicular KM desde K hasta AG, y unir GΘ, AK y AΘ. Nuevamente, tomémoslo como dado, desde lo que anteriormente fue probado, que
GK = KΘ = 84;52p donde la hipotenusa GΘ = 120p.
Luego, primero, para Saturno:
Dado que demostramos que el radio del Epiciclo es de 6;30p donde la distancia media es de 60p,
GK = KΘ = 4;36p donde la hipotenusa GΘ = 6;30p.
Y ya que, por hipótesis, el ángulo de la inclinación del epiciclo,
el ^ AGE = 4;30º donde 4 ángulos rectos = 360º
el ^ AGE = 9ºº donde 2 ángulos rectos = 360º,
en el círculo alrededor del triángulo rectángulo GKM,
arco KM = 9º
y arco GM = 171º (suplementario).
Entonces las cuerdas correspondientes
KM = 9;25p donde la hipotenusa GK = 120p.
y GM = 119;38p donde la hipotenusa GK = 120p.
Por lo tanto, donde GK = 4;36p,
KM = 0;22p
y GM = 4;35p.
Ahora en la máxima inclinación sobre el semicírculo conteniendo el apogeo, AG, representando la distancia [cuando el epiciclo esta] cerca del comienzo de Libra [5], es calculada, por medio de los teoremas que hemos revisado anteriormente, en el tratamiento de las anomalías, como de 62;10p en las mismas unidades [6]. Por consiguiente, por sustracción [de GM desde AG],
AM = 57;35p donde la línea MK = 0;22p;
Por consiguiente la hipotenusa AK [= (AM² + MK²) ^ 0,5] = 57;35p en las mismas unidades.
Por lo tanto, donde la hipotenusa AK = 120p, KM = 0;46p,
y el ^ KAM [7] = 0;44ºº donde 2 ángulos rectos = 360ºº.
Pero, por hipótesis, el ángulo de la inclinación de la excéntrica,
el ^ BAG = 2;30º donde 4 ángulos rectos = 360º
el ^ BAG = 5ºº donde 2 ángulos rectos = 360ºº.
Por lo tanto, por adición, el ^ BAK = 5;44ºº donde 2 ángulos rectos = 360ºº.
Por lo tanto, en el círculo alrededor del triángulo rectángulo BAK,
arco BK = 5;44º
y arco AB = 174;16º (suplementario).
Entonces las cuerdas correspondientes
BK = 6;0p donde la hipotenusa AK = 120p
y AB = 119;51p donde la hipotenusa AK = 120p.
Por lo tanto, donde la línea AK = 57;35p,
BK = 2;53p,
AB = 57;31p,
y BL = KΘ = 4;36p [demostración luego de la Fig. T.].
Y dado que AB² + BL² = AL²,
AL = 57;42p en las mismas unidades.
Similarmente, dado que LΘ = BK = 2;53p en las mismas unidades,
y AL² + LΘ² = AΘ²,
AΘ = 57;46p.
Por lo tanto, donde la hipotenusa AΘ = 120p, ΘL = 5;59p,
y el ángulo de la desviación en latitud,
el ^ ΘAL = 5;44ºº donde 2 ángulos rectos = 360ºº
el ^ ΘAL = 2;52º donde 4 ángulos rectos = 360º.
Estos [2;52º] es lo que entraremos en la tercera columna de la tabla de Saturno opuestos a los '135º'.
Pero en la máxima inclinación sobre el semicírculo conteniendo el perigeo, dado que AG, representando la distancia [cuando el epiciclo esta] cerca del comienzo de Aries, es calculado como de 57;40p [8],
donde, como demostramos [demostración luego de la Fig. T.], KM = 0;22p y GM = 4;35p,
por consiguiente, por sustracción, AM = 53;5p.
Y la hipotenusa AK = 53;5p en las mismas unidades, dado que este es insignificantemente mayor que la línea AM.
Por lo tanto, donde la hipotenusa AK = 120p,
KM = 0;50p,
y el ^ KAM = 0;48ºº donde 2 ángulos rectos = 360ºº.
Pero, por hipótesis, el ^ BAG = 5ºº en las mismas unidades.
Entonces, por suma, y el ^ BAK = 5;48ºº donde 2 ángulos rectos = 360ºº.
Por lo tanto, en el circulo alrededor del triángulo rectángulo BAK,
arco BK = 5;48º
y arco AB = 174;12º (suplementario).
Entonces las cuerdas correspondientes
BK = 6;4p donde la hipotenusa AK = 120p
y AB = 119;51p donde la hipotenusa AK = 120p.
Por lo tanto, donde la línea AK = 53;5p,
BK = 2;41p
y AB = 53;1p.
Y dado que AB² + BL² = AL²,
y BL fue demostrado ser de 4;36p en las mismas unidades,
AL = 53;13p en las mismas unidades.
Por lo tanto, donde la hipotenusa AL = 120p, BL = 10;23p,
y el ángulo de la ecuación en longitud,
el ^ BAL = 9;56ºº donde 2 ángulos rectos = 360ºº
el ^ BAL = 4;58º donde 4 ángulos rectos = 360º.
Nuevamente, donde la línea AL = 53;13p,
ΘL = KB = 2;41p,
y AL² + ΘL² = AΘ²,
entonces AΘ = 53;17p.
Por lo tanto donde la hipotenusa AΘ = 120p, ΘL = 6;3p,
y el ángulo de la desviación en latitud,
el ^ ΘAL = 5;46ºº donde 2 ángulos rectos = 360ºº
el ^ ΘAL = 2;53º donde 4 ángulos rectos = 360º.
Estos [2;53º] es lo que entraremos en la cuarta columna de la tabla opuestos a los '135º'.
Entonces con el fin de comparar las ecuaciones en longitud para la inclinación cercana al perigeo, sea dibujado nuevamente el diagrama sin inclinación [Fig. 13.7]. Entonces, donde la distancia en aquel punto,
AG = 57;40p,
GK (= KΘ) es dado como de 4;36p;
y, por sustracción, AK = 53;4p en las mismas unidades;
Pero AK² + KΘ² = AΘ²,
Entonces AΘ = 53;16p.

Por lo tanto, donde la hipotenusa AΘ = 120p, KΘ = 10;22p,
y el ángulo de la ecuación en longitud,
el ^ ΘAK = 9;54ºº donde 2 ángulos rectos = 360ºº
el ^ ΘAK = 4;57º donde 4 ángulos rectos = 360º.
Pero cuando las inclinaciones [de la excéntrica y del epiciclo] fueron tomadas en cuenta fue demostrado ser de 4;58º. Entonces la ecuación en longitud calculada de acuerdo a ambas inclinaciones fue de 1' mayor.
Lo que se ha requerido para examinar.
Demostración de las posiciones en latitud para Júpiter
Sea allí nuevamente dibujado [Fig. 13.8], primero, el diagrama para las inclinaciones, representando las proporciones establecidas para Júpiter.
Por lo tanto, donde el radio del epiciclo, GΘ = 11;30p,
GK (= KΘ) es calculado como [84;52 * 11;30 / 120 =] 8;8p.

Entonces, ya que el ángulo de la inclinación del epiciclo,
el ^ AGE = 2;30º donde 4 ángulos rectos = 360º
el ^ AGE = 5ºº donde 2 ángulos rectos = 360ºº,
En el círculo alrededor del triángulo rectángulo GKM,
arco KM = 5º
y arco GM = 175º (suplementario).
Entonces las cuerdas correspondientes
KM = 5;14p donde la hipotenusa GK = 120p
y GM = 119;53p donde la hipotenusa GK = 120p.
Por lo tanto, donde la línea GK = 8;8p,
y AG, la distancia cerca del comienzo de Libra, es de 62;30p [9],
KM = 0;21p,
GM = 8;8p,
y, por sustracción, MA = 54;22p.
Por consiguiente la hipotenusa AK, siendo insignificantemente mayor que MA, es de 54;22p en las mismas unidades.
Por lo tanto, donde la hipotenusa AK = 120p, KM = 0;46p,
y el ^ KAM = 0;44ºº donde 2 ángulos rectos = 360ºº.
Pero, por hipótesis, el ángulo de la inclinación de la excéntrica,
el ^ BAG = 1;30º donde 4 ángulos rectos = 360º.
el ^ BAG = 3ºº donde 2 ángulos rectos = 360ºº.
Por lo tanto, por adición, el ^ BAK = 3;44ºº donde 2 ángulos rectos = 360ºº.
Por lo tanto, en el círculo alrededor del triángulo rectángulo BAK,
arco KB = 3;44º
y arco AB = 176;16º (suplementario).
Entonces las cuerdas correspondientes
KB = 3;54p donde la hipotenusa AK = 120p.
Y AB = 119;56p donde la hipotenusa AK = 120p.
Por lo tanto, donde la línea, AK = 54;22p,
KB = 1;46p
y AB = 54;20p.
Y, de lo que hemos demostrado previamente, BL = 8;8p en las mismas unidades.
Y dado que AB² + BL² = AL²,
AL = 54;56p en las mismas unidades.
Similarmente, ya que LΘ [= KB] = 1;46p en las mismas unidades,
y AL² + LΘ² = AΘ²,
AΘ = 54;58p en las mismas unidades.
Por consiguiente, donde la hipotenusa AΘ = 120p, LΘ = 3;52p,
y el ángulo de la desviación en latitud,
el ^ ΘAL = 3;42ºº donde 2 ángulos rectos = 360ºº
el ^ ΘAL = 1;51º donde 4 ángulos rectos = 360º.
Este [1;51º] es lo que entraremos en la tercera columna de la tabla de Júpiter opuesto a los '135º'.
En el mismo sentido, AG, cuando representa la distancia al comienzo de Aries, es calculado como de 57;30p [10], donde, como demostramos, KM = 0;21p y GM = 8;8p;
por consiguiente, AM (= AK que es insignificantemente mayor) es de 49;22p en las mismas unidades.
Por lo tanto, donde la hipotenusa AK = 120p, KM = 0;51p,
y el ^ KAM = 0;49ºº donde 2 ángulos rectos = 360ºº.
Por lo tanto, por adición, el ^ BAK [= ^ KAM + 3ºº] = 3;49ºº en las mismas unidades.
Por lo tanto, en el círculo alrededor del triángulo rectángulo AKB,
arco KB = 3;49º
y arco AB = 176;11º (suplementario).
Entonces las cuerdas correspondientes
BK = 3;59p donde la hipotenusa AK = 120p
y AB = 119;56p donde la hipotenusa AK = 120p.
Por lo tanto, donde la línea AK = 49;22p,
KB = 1;39p
y AB = 49;20p.
Por consiguiente, dado que BL = 8;8p en las mismas unidades,
y AB² + BL² = AL²,
AL = 50;0p en las mismas unidades.
Por lo tanto, donde la hipotenusa AL = 120p, BL = 19;31p,
y el ángulo de la ecuación en longitud,
el ^ BAL = 18;44º donde 2 ángulos rectos = 360ºº
el ^ BAL = 9;22º donde 4 ángulos rectos = 360º.
Nuevamente, donde la línea AL = 50;0p,
ΘL [= KB] = 1;39p,
y AL² + ΘL² = AΘ²,
entonces AΘ = 50;2p.
Por lo tanto, donde la hipotenusa AΘ = 120p, LΘ = 3;57p,
y el ángulo de la desviación en latitud,
el ^ ΘAL = 3;46ºº donde 2 ángulos rectos = 360ºº
el ^ ΘAL = 1;53º donde 4 ángulos rectos = 360º.
Este [1;53º] es lo que entraremos en la cuarta columna de la tabla opuesto al mismo '135º'.
Con el fin de comparar las ecuaciones en longitud, sea dibujado [Fig. 13.9] nuevamente el diagrama con ninguna inclinación. Luego, en la distancia en cuestión,
donde ΘK = GK = 8;8p,
la línea total AG = 57;30p,
y, por sustracción, AK = 49;22p en las mismas unidades.
Pero AK² + KΘ² = AΘ²,
entonces AΘ = 50;2p en las mismas unidades.
Por lo tanto, donde la hipotenusa AΘ = 120p, ΘK = 19;30p,
y el ángulo de la ecuación en longitud,
el ^ ΘAK = 18;42ºº donde 2 ángulos rectos = 360ºº
el ^ ΘAK = 9;21º donde 4 ángulos rectos = 360º.
Y cuando las inclinaciones fueron tomadas en cuenta fue demostrado ser de 9;22º. Entonces la ecuación en longitud calculada de acuerdo a ambas inclinaciones fue, nuevamente, mayor por solo un único minuto.
Lo que se ha requerido para examinar.
Demostración de las posiciones en latitud para Marte
Seguidamente, para determinar las cantidades para Marte, primero, sea allí dibujado el diagrama [Fig. 13.10] para las inclinaciones, y sea GK (= KΘ) calculado como [84;52 * 39;30 / 120 =] 27;56p, donde el radio del epiciclo, GΘ = 39;30p.

Entonces, dado que el ángulo de inclinación del epiciclo,
el ^ AGE = 2;15º donde 4 ángulos rectos = 360º
el ^ AGE = 4;30ºº donde 2 ángulos rectos = 360ºº,
en el círculo alrededor del triángulo rectángulo GMK,
arco KM = 4;30º
y arco GM = 175;30º (suplementario).
Entonces las cuerdas correspondientes
KM = 4;43p donde la hipotenusa GK = 120p
y GM = 119;54p donde la hipotenusa GK = 120p.
Por lo tanto, donde la línea GK = 27;56p,
y AG, la distancia máxima, es de 66p [11],
KM = 1;6p
y GM = 27;54p,
y, por sustracción, AM = 38;6p.
Por lo tanto la hipotenusa AK [= (AK² + KM²) ^ 0,5] = 38;7p en las mismas unidades.
Por consiguiente, donde la hipotenusa AK = 120p,
KM = 3;28p,
y el ^ KAM = 3;19ºº donde 2 ángulos rectos = 360ºº.
Pero, por hipótesis, el ángulo de inclinación de la excéntrica,

el ^ BAG = 1º donde 4 ángulos rectos = 360º
el ^ BAG = 2ºº donde 2 ángulos rectos = 360ºº.
Por lo tanto, por adición, el ^ BAK = 5;19ºº donde 2 ángulos rectos = 360ºº.
Entonces, en el círculo alrededor del triángulo rectángulo BAK,
arco KB = 5;19º
y arco AB = 174;41º (complementario [(?) ¡es suplementario!]).
Entonces las cuerdas correspondientes
BK = 5;34p donde la hipotenusa AK = 120p
BK = 119;52p donde la hipotenusa AK = 120p.
Por lo tanto, donde la línea AK = 38;7p,
KB = 1;46p
y AB = 38;5p.
Pero la línea BL [= KΘ = GK] = 27;56p en las mismas unidades.
Y, dado que AB² + BL² = AL²,
AL = 47;14p.
Similarmente, dado que ΘL = 1;46p en las mismas unidades,
y AL² + LΘ² = AΘ²,
AΘ = 47;16p en las mismas unidades.
Por lo tanto, donde la hipotenusa AΘ = 120p, ΘL = 4;29p,
y el ángulo de la desviación en latitud,
el ^ ΘAL = 4;18ºº donde 2 ángulos rectos = 360ºº
el ^ ΘAL = 2;9º donde 4 ángulos rectos = 360º.
Estos [2;9º] es lo que entraremos en la tercera columna de la tabla para Marte opuestos a los '135º'.
En el mismo sentido, para las inclinaciones en la mínima distancia:
AG = 54p donde, como fue demostrado,
KM = 1;6p
y GM = 27;54p.
Por consiguiente, por sustracción, AM = 26;6p,
y la hipotenusa AK [= (KM² + AM²) ^ 0,5] = 26;7p en las mismas unidades.
Por lo tanto, donde la hipotenusa AK = 120p, KM = 5;3p,
y el ^ KAM = 4;49ºº donde 2 ángulos rectos = 360ºº.
Por consiguiente, por adición, el ^ BAK = 6;49ºº en las mismas unidades.
Por lo tanto, en el círculo alrededor del triángulo rectángulo ABK,
arco BK = 6;49º
y arco AB = 173;11º (suplementario).
Entonces las cuerdas correspondientes
BK = 7;8p donde la hipotenusa AK = 120p
y AB = 119;47p donde la hipotenusa AK = 120p.
Por lo tanto, donde la línea AK = 26;7p,
BK = 1;33p
y AB = 26;4p.
Y la línea BL es, nuevamente, 27;56p en las mismas unidades.
Y, dado que AB² + BL² = AL², AL = 38;12p.
Por lo tanto, donde la hipotenusa AL = 120p, BL = 87;45p,
y el ángulo de la ecuación en longitud,
el ^ BAL = 94ºº donde 2 ángulos rectos = 360ºº
el ^ BAL = 47º donde 4 ángulos rectos = 360º.
Similarmente, donde la línea AL = 38;12p, LΘ [= BK] = 1;33p,
y AL² + LΘ² = AΘ²,
entonces AΘ = 38;14p.
Por lo tanto, donde la hipotenusa AΘ = 120p, LΘ = 4;52p,
y el ángulo de la desviación en latitud,
el ^ ΘAL = 4;40ºº donde 2 ángulos rectos = 360ºº
el ^ ΘAL = 2;20º donde 2 ángulos rectos = 360º.
Estos [2;20º] es lo que entraremos en la cuarta columna de la tabla opuestos al mismo '135º'.
Nuevamente, si, con el fin de comparar las ecuaciones en longitud, establecemos el diagrama [Fig. 13.11] sin las inclinaciones, en la mínima distancia (donde la diferencia necesariamente debe ser mas notable),
AG / GK (= KΘ) = 54 / 27;56.
Por consiguiente, por sustracción, AK = 26;4p,
y la hipotenusa AΘ [= (AK² + KΘ²) ^ 0,5] = 38;12p en las mismas unidades.
Por consiguiente, donde la hipotenusa AΘ = 120p,
ΘK = 87;45p nuevamente [como BL en los cálculos previos],
y el ángulo de la ecuación en longitud,
el ^ ΘAK = 94ºº donde 2 ángulos rectos = 360ºº
el ^ ΘAK = 47º donde 4 ángulos rectos = 360º.

Pero este [ángulo] es del mismo tamaño como fue demostrado por medio de los cálculos incluyendo las inclinaciones. Por lo tanto la ecuación en longitud para Marte calculada de acuerdo a las inclinaciones de los círculos [del epiciclo y de la excéntrica] no difiere del todo.
Lo que se ha requerido para examinar.
Demostración de la máxima desviación en Latitud para las Máximas y Mínimas distancias de Mercurio y Venus
La cuarta columna en las dos tablas para Venus y Mercurio contendrá las posiciones en latitud producidas por las máximas oblicuidades de sus epiciclos, que ocurren en el apogeo y en el perigeo de la excéntrica. No obstante, las hemos calculado separadamente, sin el efecto debido a la inclinación de la excéntrica, dado que esta podría haber requerido un mayor número de tablas y un método más complicado de cálculo [desde las tablas]: para las posiciones [latitudinales correspondientes] como estrella de la mañana y de la tarde que no van a ser iguales una con la otra, e incluso no siempre sobre el mismo lado [por ej. al Norte o al Sur] de la eclíptica; y en cualquier caso, dado que la inclinación de la excéntrica no es constante, las diferencias en la cantidad a ser disminuidas con respecto a la máxima inclinación [del epiciclo] podrían no corresponder a las diferencias en la cantidad a ser disminuidas con respecto a la máxima oblicuidad [12]. Sin embargo, si separamos los efectos, podemos determinar cada elemento por un camino más conveniente, como llegará [a ser] claro desde los presentes procedimientos que vamos a brindar.
Sea AB [ver la Fig. 13.12] la intersección de los planos de la eclíptica y del epiciclo. Sea A el punto tomado como el centro de la eclíptica, y B como centro del epiciclo, y sea GDEZH el epiciclo descrito alrededor de su oblicuidad al plano de la eclíptica [13], por ej. de modo que las líneas rectas dibujadas en los [dos planos] perpendiculares a la sección común GH todos forman ángulos iguales en los puntos sobre GH. Dibujar AE tangente al epiciclo, y AZD intersecando el epiciclo en un punto arbitrario, y eliminar desde los puntos D, E y Z las perpendiculares DΘ, EK y ZL hasta GH, y las perpendiculares DM, EN y ZX hasta el plano de la eclíptica. Unir ΘM, KN, LX, y también AN y AXM (dado que AXM estará en una línea recta, dado que los tres puntos [A, X y M todos] se ubican en dos planos, el plano de la eclíptica y el plano a través de AZD perpendicular a la eclíptica.

Es obvio que, con la oblicuidad descrita, las ecuaciones en longitud del planeta [en los puntos D y E respectivamente] estarán representadas por los ángulos ΘAM y KAN, y las [posiciones] en latitud por los ángulos DAM y EAN. Primero, debemos demostrar que la posición en latitud en el punto tangente, el ^ EAN, es el máximo, justamente como la ecuación en longitud [es la máxima en este punto].
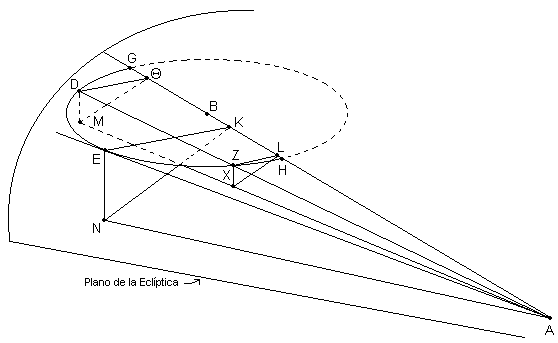
[Demostrar:] Dado que el ^ EAK es el máximo,
KE / EA > ΘD / DA = LZ / ZA.
Pero EK / EN = ΘD / DM = LZ / ZX,
ya que, como dijimos, los triángulos formados por ellos [EKN, DΘM y ZLX] tienen ángulos iguales [en GH] y ángulos rectos en M, N y X.
En consecuencia NE / EA > MD / DA = XZ / ZA.
Y, nuevamente, los ángulos DMA, ENA y ZXA son rectos.
Inmediatamente es obvio que, cuando uno considera el efecto sobre las ecuaciones en longitud causado por la oblicuidad, la máxima diferencia es producida en las máximas desviaciones en latitud en E. Porque las diferencias [en la ecuación causadas por la oblicuidad] están representadas por los ángulos subtendidos por (ΘD - ΘM), (KE - KN) y (LZ - LX) [cuando el planeta esta en D, E y Z respectivamente], y dado que las proporciones de esas líneas [ΘD / ΘM, etc.] entre sí con la diferencia entre ellos [(ΘD - ΘM), etc.] se mantienen iguales, sigue que
(EK - KN) / EA > (ΘD - ΘM) / AD, etc. [14].
Y también es inmediatamente claro que, mientras la proporción entre la máxima ecuación en longitud con la máxima desviación en latitud [debido a la oblicuidad], esta proporción mantiene la ecuación en longitud para cualquier posición [del planeta] sobre el epiciclo y la posición [correspondiente] en latitud.
Dado que KE / EN = LZ / ZX = ΘD / DM,
Y así sucesivamente para los otros puntos [sobre el epiciclo] [15].
Lo que se ha requerido para examinar.
Habiendo establecido estos puntos preliminares, examinemos primero el tamaño del ángulo que esta contenido por la oblicuidad de los planos para cada uno de los dos planetas. Damos por garantizado que esto fue señalado al comienzo (de la discusión al principio del Libro XIII Capítulo 3), de que ambos planetas, cuando [están] a medio camino entre las máximas y mínimas distancias, visualizan una máxima diferencia [en latitud] entre las posiciones opuestas sobre el epiciclo por 5º hacia el Norte o hacia el Sur: por lo que para Venus parece variar levemente por más de 5º en el perigeo y [variar] levemente por menos que 5º en el apogeo, mientras que para Mercurio varía alrededor de ½º [más o menos respecto de los 5º en los 180º desde el apogeo [(¿apogeo? = perigeo)] y del apogeo respectivamente].
Sea nuevamente ABG la intersección de la eclíptica con el epiciclo [Fig. 13.13]. Describir el epiciclo GDE alrededor del centro B, oblicuo al plano de la eclíptica [16] por el camino [ya] descrito. Desde A, el centro de la eclíptica, dibujar AD tangente al epiciclo, y desde D eliminar la perpendicular DZ encima de GBE, y la perpendicular DH al plano de la eclíptica. Unir BD, ZH y AH, y sea el ^ DAH tomado como comprendiendo la mitad de la desviación en latitud anterior (de arriba) para cada uno de los dos planetas (en consecuencia este [^ DAH] es de 2 ½º).

Sea nuestro problema, encontrar para cada uno la cantidad de la oblicuidad entre los planetas, a saber el tamaño del ^ DZH.
Para Venus, ya que, donde el radio del epiciclo es de 43;10p, la máxima distancia es de 61;15p, la mínima 58;45p, y la media entre ellas de 60p,
AB / BD = 60 / 43;10.
Y desde que AB² - BD² = AD²,
AD = 41;40p en la mismas unidades.
Similarmente, dado que BA / AD = BD / DZ,
DZ = 29;58p en las mismas unidades.
Además, dado que, por hipótesis,
el ^ DAH = 2;30º donde 4 ángulos rectos = 360º
el ^ DAH = 5ºº donde 2 ángulos rectos = 360ºº,
en el círculo alrededor del triángulo rectángulo ADH,
arco DH = 5º
y la correspondiente cuerda DH = 5;14p donde la hipotenusa AD = 120p.
Por lo tanto, donde la línea AD = 41;40p, DH = 1;50p.
Y DZ fue demostrado ser de 29;58p en las mismas unidades.
Por lo tanto, donde la hipotenusa DZ = 120p, DH = 7;20p,
y el ángulo de la oblicuidad,
el ^ DZH = 7ºº donde 2 ángulos rectos = 360ºº
el ^ DZH = 3;30º donde 4 ángulos rectos = 360º [17].
Pero dado que la cantidad por la que el ^ DAZ excede al ^ HAZ representa la diferencia resultante en la ecuación en longitud, debemos inmediatamente calcular esto también, encontrando las cantidades de esos ángulos. Ya que demostramos que, donde la línea DH = 1;50p, la hipotenusa AD = 41;40p y DZ = 29;58p;
y AD² - DH² = AH²
mientras ZD² - DH² = HZ²;
entonces AH = 41;37p
y HZ = 29;55p en las mismas unidades.
Por lo tanto, donde la hipotenusa AH = 120p, ZH = 86;16p,
y el ^ ZAH = 91;56ºº donde 2 ángulos rectos = 360ºº
y el ^ ZAH = 45;58º donde 4 ángulos rectos = 360º.
Similarmente, dado que DZ = 86;18p donde la hipotenusa AD = 120p,
el ^ DAZ = 91;58ºº donde 2 ángulos rectos = 360ºº
el ^ DAZ = 45;59º donde 4 ángulos rectos = 360º.
De este modo la ecuación en longitud calculada de acuerdo a la oblicuidad fue menor que un minuto.
Para Mercurio [ver Fig. 13.14], donde el radio del epiciclo es de 22;30p, la máxima distancia, como demostramos, es de 69p, y la distancia diametralmente opuesta a ella [69p] de 57p; la media entre esas dos es calculada como en 63p en las mismas unidades.
Entonces AB / BD = 63 / 22;30.
Y dado que AB² - DB² = AD²,
AD = 58;51p.

Similarmente, dado que AB / AD = BD / DZ,
DZ = 21;1p en las mismas unidades.
Nuevamente, dado que, por hipótesis,
el ^ DAH = 5ºº donde 2 ángulos rectos = 360ºº,
en el círculo alrededor del triángulo rectángulo ADH,
arco DH = 5º,
y la cuerda correspondiente DH = 5;14p donde la hipotenusa AD = 120p.
Por lo tanto, donde la línea AD = 58;51p, DH = 2;34p.
Pero demostramos que DZ = 21;1p en las mismas unidades.
Por lo tanto, donde la hipotenusa DZ = 120p, DH = 14;40p,
y el ángulo de la oblicuidad,
el ^ DZH = 14ºº donde 2 ángulos rectos = 360ºº
el ^ DZH = 7º donde 4 ángulos rectos = 360º [18].
Por el mismo camino [como para Venus], con el fin de comparar los ángulos de la ecuación [en longitud]:
nuevamente, donde DH = 2;34p, demostramos que
la hipotenusa AD = 58;51p y DZ = 21;1p.
y DA² - DH² = AH²,
DZ² - DH² = HZ²,
entonces AH = 58;47p
y ZH = 20;53p en las mismas unidades.
Por lo tanto, donde la hipotenusa AH = 120p, HZ = 42;38p,
y el ^ ZAH = 41;38ºº donde 2 ángulos rectos = 360ºº
y el ^ ZAH = 20;49º donde 4 ángulos rectos = 360º.
En el mismo sentido, donde la hipotenusa AD = 120p, DZ es calculada como 42;50p,
y el ^ DAZ = 41;50ºº donde 2 ángulos rectos = 360ºº
y el ^ DAZ = 20;55º donde 4 ángulos rectos = 360º.
Entonces en este caso la ecuación en longitud debido a la oblicuidad fue menor que 6' [19].
Lo que se ha requerido para examinar.
Seguidamente examinemos, si tomamos las cantidades anteriores de la oblicuidad como dadas, encontramos las máximas latitudes en las máximas y en las mínimas distancias [derivadas desde ellas] de acuerdo con aquellas derivadas desde nuestras observaciones. En la misma figura [fig. 13.15], ahora tomemos como base la máxima distancia de Venus, por ej.

AB / BD = 61;15 / 43;10.
Por consiguiente, dado que AB² - BD² = AD²,
AD = 43;27p.
Pero AB / AD = BD / DZ.
Entonces DZ = 30;37p en las mismas medidas.
Nuevamente, dado que, por hipótesis, el ángulo de la oblicuidad,
el ^ DZH = 7ºº donde 2 ángulos rectos = 360ºº
y [por consiguiente] DH = 7;20p donde la hipotenusa DZ = 120p,
por lo tanto, donde la línea DZ = 30;37p, y AD = 43;27p,
DH = 1;52p.
Entonces donde la hipotenusa AD = 120p,
DH = 5;9p,
Y la máxima desviación en latitud,
el ^ DAH = 4;54ºº donde 2 ángulos rectos = 360ºº
el ^ DAH = 2;27º donde 4 ángulos rectos = 360º.
Pero en la mínima distancia, donde el radio del epiciclo,
BD = 43;10p,
AB es dado como de 58;45p.
Y AB² - DB² = AD²,
entonces AD = 39;51p en las mismas unidades.
Similarmente, dado que AB / AD = BD / DZ,
DZ = 29;17p en las mismas unidades.
Pero DZ / DH es dada como 120 / 7;20.
Por lo tanto, donde DZ = 29;17p y AD = 39;51p,
Pero DH = 1;47p.
Por lo tanto, donde la hipotenusa AD = 120p, DH = 5;22p,
y la máxima desviación en latitud,
el ^ DAH = 5;8ºº donde 2 ángulos rectos = 360ºº
el ^ DAH = 2;34º donde 4 ángulos rectos = 360º.
En consecuencia [la máxima latitud] difiere 2 ½º de la [máxima] desviación en latitud asumida para la media, siendo menor en el apogeo y mayor en el perigeo, pero [en ambos casos] por una cantidad que es insignificante a los sentidos; dado que para la máxima distancia, esta fue menor solamente por tres minutos, y en la mínima distancia por cuatro minutos más. Tales [pequeñas diferencias] no pueden ser del todo fácilmente detectadas desde las observaciones.
Seguido, [Fig. 13.16] tomemos la máxima distancia de Mercurio como base, a saber
AB / BD = 69 / 22;30.
Por consiguiente, por el mismo procedimiento como el anterior,
AD [= (AB² - BD²) ^ 0,5] = 65;14p,
y DZ [= AD * BD / AB] = 21;16p en las mismas unidades.
Pero en este caso el ángulo de la oblicuidad,
el ^ DZH es dado como de 14ºº donde 2 ángulos rectos = 360ºº.
Por consiguiente tenemos DH = 14;40p [20] donde la hipotenusa DZ = 120p.
Por lo tanto, donde la línea DZ = 21;16p, y AD = 65;14p,
DH = 2;36p.
Por lo tanto, donde la hipotenusa AD = 120p, DH = 4;47p,
y la desviación máxima en latitud,
el ^ DAH = 4;34ºº donde 2 ángulos rectos = 360ºº
el ^ DAH = 2;17º donde 4 ángulos rectos = 360º.

Pero en la distancia mínima [21],
AB / BD es dada como de 57 / 22;30,
y entonces, por el mismo procedimiento nuevamente,
AD = 52;22p en las mismas unidades
y DZ = 20;40p.
Y la oblicuidad es la misma como la anterior,
y por consiguiente ZD / DH es dada como 120 / 14;40,
entonces donde DZ = 20;40p y AD = 52;22p,
DH = 2;32p.
Por lo tanto, donde la hipotenusa AD = 120p, DH = 5;48p.
el ^ DAH = 5;32ºº donde 2 ángulos rectos = 360ºº
el ^ DAH = 2;46º donde 4 ángulos rectos = 360º.
Por lo tanto, la diferencia desde la máxima desviación en latitud sobre la media (aquí también fue tomada como de 2 ½º) fue de 13' en la dirección negativa en el apogeo y de 16' en la dirección positiva en el perigeo. Para representar esto, usaremos una corrección de ¼º con respecto a la media en los cálculos [desde la tabla], de acuerdo con la diferencia perceptible derivada desde las observaciones.
Ahora que hemos demostrado lo de arriba, y también demostrado que la proporción entre la máxima ecuación en longitud con la máxima desviación en latitud también se mantiene [muy] bien en otros puntos en el epiciclo para la proporción entre las ecuaciones individuales en longitud y las [correspondientes] posiciones individuales en latitud [22], inmediatamente tenemos un método conveniente para calcular las posiciones en latitud debido a la oblicuidad a ser entradas en la cuarta columna de las tablas para Venus y Mercurio. No obstante, como mencionamos, esas posiciones están basadas solamente sobre la oblicuidad de los epiciclos en la distancia media: la diferencia debido a la inclinación de las excéntricas, y también a la diferencia debido a [la aproximación hasta] el apogeo o el perigeo para Mercurio serán halladas [desde las tablas] por medio de un procedimiento de corrección en el cómputo, para una conveniencia en el cálculo.
Dado que, en las distancias medias establecidas anteriormente, la máxima desviación debida a la oblicuidad fue demostrada ser de 2;30º a ambos lados de la eclíptica para ambos planetas; y la máxima ecuación en longitud es de aproximadamente 46º para Venus y 22º para Mercurio [23]; y ya, hemos establecido en las tablas para la anomalía de esos planetas, las ecuaciones correspondientes a las posiciones individuales en el epiciclo. Entonces formamos las proporciones entre esto último y la máxima ecuación, tomando la misma proporción de 2 ½º, separadamente para cada planeta, y entramos los resultados en la cuarta columna de las tablas de latitud opuestos a los argumentos correspondientes.
(En cada tabla) hemos producido [(agregado)] la quinta columna con el fin de corregir las posiciones en latitud para otras posiciones [del epiciclo] sobre la excéntrica, utilizando las sexagésimas entradas [en esa columna]. Porque, como dijimos, dado que el incremento y la disminución en la inclinación y en la oblicuidad del epiciclo, a través de la acción de los pequeños círculos unidos, precisamente tienen un período correspondiente al período de una vuelta sobre la excéntrica, y dado que las cantidades de todas las inclinaciones y oblicuidades no son muy diferentes de aquellas asociadas con la órbita inclinada de la Luna, y las desviaciones individuales en latitud, para tales pequeñas inclinaciones, son, nuevamente, también proporcionales, y ya que tenemos las entradas correspondientes para la Luna calculadas geométricamente, multiplicamos por 12 cada una de las entradas en esta tabla (porque la máxima allí es de alrededor de 5º, y aquí la máxima la estamos haciendo de 60), y entramos los resultados opuestos al argumento apropiado en la quinta columna de cada tabla.
El diseño de las tablas es el siguiente.
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Libro XIII |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 | 11 |
Notas de referencia
- ↑ Notar que G no es un punto sobre el epiciclo, como podría aparecer en la Fig. 13.2 y en la figura correspondiente a Mercurio, Fig. 13.4. Para hacer que los diferentes planos en esta figura tridimensional sean más claros se han redibujado en la figura S.
- ↑ Ver la Fig. S que hace mas obvia la exposición de Ptolomeo. En particular, dado que M esta en la eclíptica (por construcción) y el ^ AMΘ es construido como un ángulo recto, LM, KΘ y BH son todos paralelos, entonces el ^ ALM es un ángulo recto.
- ↑ Uno encuentra, exactamente, 45;59º (al minuto más cercano) con la inclinación, y 46;0º sin él. Aquí la imprecisión de Ptolomeo es un misterio, dado que para la Tabla de la Anomalía, [con] el argumento 135º en la distancia media, él encuentra el mejor valor de 45;59º (probablemente por un calculo idéntico).
- ↑ De hecho este último número no ha sido verificado previamente. No obstante, Ptolomeo debe haber calculado las distancias por todo el "camino" alrededor de la órbita con el fin de construir la Tablas de las Anomalías, y sin duda se encontró este valor por interpolación. Neugebauer (HAMA 221) encontró 56;37p desde una ecuación cúbica. Sin embargo, con un programa de computadora encuentro, para seg. κ = 93;1,41º, κ₀ = 90;0,0, ρ = 56;43,9p.
- ↑ Cf. a mitad del Libro XIII Capítulo 1.
- ↑ Exactamente, 62;8,21p cuando el centro del epiciclo esta en longitud verdadera de ♎︎ 0º (el apogeo estando en ♏︎ 20º, cf. Libro XIII Capítulo 6).
- ↑ Leer KAM en cambio de KΛM (error de impresión en el texto de Heiberg en H554,11). Corregido por Manitius.
- ↑ Exactamente, 57;44,48p cuando el centro del epiciclo esta en una longitud de ♈︎ 0º. Precisamente opuesta a la distancia de ρ = 62;10p es la distancia (63;25 * 56;35 / 62;10 =) 57;43p. Es obvio que Ptolomeo ha redondeado convenientemente a un número más cercano, sea cual fuere el método de cálculo que ha utilizado.
- ↑ Exactamente, 62;34,36p cuando el centro del epiciclo esta en la longitud verdadera de ♎︎ 0º (el apogeo estando en ♍︎ 10º, cf. Libro XIII Capítulo 6).
- ↑ Exactamente 57;24,31p. Los valores de Ptolomeo para ambas distancias (cf. nota de referencia anterior) podrían ajustarse mejor a una elongación desde el apogeo de -24 ½º y (180º - 24 ½º), mas bien que los -20º que él especifica en el Libro XIII Capítulo 6. Pero si uno fuera a tomar la posición exacta del apogeo en su tiempo, ♍︎ 11º, ello podría dar -19º incluso con la peor conformidad con el texto.
- ↑ Por ej. el punto Norte esta tomado coincidiendo con el apogeo, ambos siendo ubicados en el (redondeado) ♌︎ 0º.
- ↑ Ptolomeo da a entender que uno no puede utilizar una única columna como coeficiente (c₅ en HAMA) para calcular la disminución con respecto a la máxima a ambas, inclinación y oblicuidad, como una función de la posición del planeta sobre el epiciclo.
- ↑ Ver mas abajo la Fig. U para un rediseño tridimensional de esta figura [Fig. 13.12]. Notar que la figura de Ptolomeo es una figura artificial, ya que cuando la intersección de los planos de la eclíptica y del epiciclo pasan a través del centro del epiciclo, la "oblicuidad" es cero. Aunque esto esta justificado por la "separación de los efectos".
- ↑ Aquí el argumento de Ptolomeo es erróneo, señalado por Pedersen 382. Parece haber sido engañado por su figura, que sustituye las líneas rectas por arcos.
- ↑ Esto también es erróneo, dado que Ptolomeo ha sustituido las cuerdas por arcos (en terminología moderna, ha tratado una relación entre los senos de los ángulos como una relación entre ángulos). Ver Pedersen 380-1. No obstante, si uno lo trata como una aproximación, es bastante razonable: ver mi comentario sobre Pedersen, Toomer [3] 145.
- ↑ Cf. más arriba, en nota de referencia nro. 13.
- ↑ Este "elegante" resultado solo es logrado por algún intrincado redondeo: calculando exactamente uno encuentra 3;28 ½º.
- ↑ Exactamente, 7;1º.
- ↑ Ptolomeo ha extendido un poco los cálculos para llegar a este resultado. Cálculos exactos dan el ^ ZAH = 41;33,58ºº, y el ^ DAZ = 41;50,50ºº, con una diferencia de 0;16,52ºº, o alrededor de 8 ½'.
- ↑ La cuerda de 14º (Libro I Capítulo 11) es de 14;37,27p. Pero las 14;40p de Ptolomeo están justificadas luego de la Fig. 13.14, donde los 7º de la oblicuidad son derivados desde este valor.
- ↑ Aquí Ptolomeo esta hablando vagamente. 57p no representan, la mínima distancia, (que es c. de 55;34p en 120º desde el apogeo, al final del Libro IX Capítulo 9), sino la distancia en el punto opuesto a la máxima distancia, por ej. [esto es] estrictamente análogo a la situación de Venus. Cf. el uso de "Perigeo" debajo.
- ↑ Ver más arriba la nota de referencia nro. 14.
- ↑ Esos números simplemente están redondeados desde la máxima en la columna 6 de las Tablas de las Anomalías, 45;59º para Venus y 22;2º para Mercurio. Heiberg erróneamente se refiere al Libro XII Capítulo 9, que no da nada para comparar, dado que se refiere a la elongación verdadera y no a la media.
