Almagesto: Libro VI - Capítulo 11
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
{Sobre los ángulos de Inclinación en los Eclipses}
El siguiente tema es el examen de las inclinaciones [2] que son formadas en los eclipses. Esta clase de investigación esta basada tanto en la inclinación de la parte eclipsada [del cuerpo] con la Eclíptica y en la inclinación de la eclíptica por sí misma con el Horizonte. Ambos de estos ángulos, durante el curso de cada fase del eclipse, padecen grandes cambios como resultado del desplazamiento de la posición [de los cuerpos], en el sentido que no pueden ser controlados si uno quiere emprender la tarea de calcular las inclinaciones a través de toda la duración [del eclipse], tarea superflua, dado que las predicciones sobre tal escala no son al menos necesarias o útiles. Porque, dado que la ubicación relativa de la eclíptica con el horizonte esta determinada desde su posición sobre el horizonte ocupado por sus puntos de salida o de puesta [de la eclíptica], el ángulo formado por la eclíptica en el horizonte debe necesariamente cambiar continuamente durante el curso de un eclipse, como aquellos puntos sobre la eclíptica que están continuamente cambiando saliendo o poniéndose. Similarmente, dado que la inclinación de la parte eclipsada [del cuerpo] con la eclíptica esta determinada por el gran círculo dibujado a través de los dos centros, [por ej. de] los centros de la Luna y de la Sombra o de los centros de la Luna y del Sol, esto es, nuevamente, una consecuencia necesaria del movimiento del centro de la Luna durante el curso de un eclipse tal que el círculo a través de los dos centros ocupan una posición continuamente variable relativa a la eclíptica, y [por lo tanto] el ángulo formado en su intersección varía continuamente. Por lo tanto [la necesidad para] este tipo de examen estará satisfecha si es llevada a cabo solamente por aquellos puntos en [el progreso del] eclipse que tengan algún significado, y solo toscamente por las inclinaciones con respecto al horizonte. [Para lograr este tipo de precisión] las gentes que actualmente observan el eclipse tal como ocurre pueden, meramente a ojo, estimar las inclinaciones importantes observando las posiciones relativas en ambos casos [en el eclipse y en el horizonte], dado que, como dijimos, una tosca noción [de la cantidad] es suficiente en tales asuntos. A pesar de ello, no pasaremos por alto enteramente este tema, trataremos de establecer algunos caminos para lograr el tipo de resultado deseado tan convenientemente como sea posible.
Los puntos, que merecen ser pensados significativamente, en [el progreso del] eclipse [y] que también tomamos en consideración son:
- [1] el punto del comienzo del oscurecimiento, que coincide con el principio de todo el eclipse;
- [2] el punto del [comienzo del] oscurecimiento completo, que coincide con el comienzo de la fase de la totalidad;
- [3] el punto del máximo oscurecimiento, que coincide con la mitad de la totalidad [3];
- [4] el punto del comienzo de la emersión (egreso), que coincide con el final de toda la fase total;
- [5] el punto de la emersión completa, que coincide con el final de todo el eclipse.
Las inclinaciones [con respecto al horizonte] que tomamos en consideración siendo más razonables y significativas aquellas limitadas por el Meridiano y también limitadas por los puntos de salida y de puesta de la eclíptica en los Equinoccios y en los Solsticios de verano y de invierno. En cuanto a los puntos limitando varias "direcciones de los vientos" [4], pueden ser entendidos por mucha gente por varios caminos diferentes; a pesar de ello, si lo deseamos, pueden ser señalados por medio de los ángulos que establecimos a lo largo del horizonte.
Considerando las intersecciones del meridiano con el horizonte, hagamos las siguientes definiciones:
la intersección Norte es el "punto Norte";
la intersección Sur es el "punto Sur".
Considerando las salidas y las puestas [de los puntos de la eclíptica, hagamos las siguientes definiciones]:
- las intersecciones al comienzo de Aries o de Libra con el horizonte son conocidas como la "salida equinoccial" y la "puesta equinoccial"; estos están siempre a la misma distancia, [por ej. de] un cuadrante, desde el punto donde el meridiano se interseca con [el horizonte];
- las intersecciones al comienzo de Cáncer [son conocidas] como la "salida vernal" y la "puesta vernal", y las intersecciones del comienzo de Capricornio como la "salida invernal" y la "puesta invernal".
- Las distancias [de la intersección del meridiano] con esos [cuatro] últimos puntos varían de acuerdo a la latitud en cuestión. Las inclinaciones son suficientemente caracterizadas diciendo que están en una de las ubicaciones de arriba o entre algún par de ellas.
Para permitirle a uno determinar la posición de la eclíptica relativa sobre el horizonte en cualquier situación dada, calculamos, por el método indicado en los primeros libros de nuestro tratado [5], la distancia a lo largo del horizonte, en la salida y en la puesta, del comienzo de cada signo Zodiacal desde los puntos donde el ecuador se interseca con [el horizonte, calculándolos] a ambos lados de él [por ej. hacia el Norte o hacia el Sur]. Hicimos esto para cada una de aquellas latitudes desde la 'Isla' de Meroe hasta el medio de Borístenes para lo cual tabulamos [inicialmente] los ángulos (Libro II Capítulo 13). Para proveer un medio fácil de reconocimiento topográfico [6], en cambio de una tabla, dibujamos un diagrama (Fig. 6.7) consistiendo en 8 círculos concéntricos concebidos como yaciendo en el plano del horizonte, para contener [varias] distancias y nomenclaturas para la Clímata 7.
Luego dibujamos dos líneas, a ángulos rectos una con la otra, a través de todos los círculos: una horizontal que representa la intersección de los planos del horizonte y el Ecuador, y la otra, una vertical representando la intersección del plano del horizonte con el plano del meridiano. Sobre el círculo más interior [7] escribimos, en los extremos de la línea horizontal, "Salida Equinoccial" y "Puesta Equinoccial", y en los extremos de la línea vertical, "Norte" y "Sur". Similarmente dibujamos [cuatro] líneas rectas a través de todos los círculos en iguales inclinaciones a ambos lados del Ecuador [por ej. desde la línea horizontal], y escribimos a lo largo de esta, en el séptimo espacio interlineal, la distancia del horizonte del punto Solsticial desde el Ecuador que hallamos para cada latitud (en unidades donde un cuadrante contiene 90º). En los extremos donde esas líneas se encuentran con el círculo más interno escribimos, para los del Sur, "Salida Invernal" y "Puesta Invernal", y para los del Norte, "Salida Vernal" y "Puesta Vernal". Para indicar los signos entre [los solsticios y los equinoccios] insertamos dos líneas más en cada uno de los cuatro segmentos, y [escribimos] a lo largo de esas [líneas] la distancia del horizonte desde el ecuador [mitad] del [comienzo del] signo zodiacal apropiado, agregando el nombre [símbolo zodiacal] de cada signo sobre el círculo más externo. También escribimos, a lo largo de la línea meridiana, para [cada] paralelo, su nombre [(del lugar)], la longitud [del día más largo] en horas, y la elevación del polo. Al escribir [los datos de todo lo anterior], empezamos con el [círculo] más grande, el círculo más externo para los datos de más al Norte, [y así sucesivamente] [8].
Con el fin de tener tabuladas las inclinaciones aparentes de las presentes fases con la eclíptica, por ej. los ángulos formados entre la eclíptica y el gran círculo uniendo los centros en cuestión en cada uno de los puntos significativos mencionados arriba, calculamos estos también, para las posiciones [sucesivas] de la Luna correspondientes a una diferencia de 1 Dígito de oscurecimiento. Sin embargo, hicimos solamente esto para las posiciones lunares en la distancia media (dado que es suficiente), y bajo la asunción de que aquellos arcos de la eclíptica y el círculo inclinado de la Luna que consideramos para los oscurecimientos son sensiblemente paralelos los unos con los otros.
Por ejemplo, sea AB [Fig. 6.6] la línea que representa el arco de la eclíptica, con A como el centro del Sol o de la sombra, y sea GDE la línea que representa el círculo inclinado de la Luna, G el punto en el que el centro de la Luna esta en el eclipse medio, y D como el punto en el que se encuentra el centro cuando justamente ésta esta totalmente eclipsada o justamente cerca del comienzo del egreso [emersión] desde la totalidad (por ej. cuando la Luna esta internamente tangente al círculo del cono de sombra). Sea E el punto en el cual [esta ubicado] el centro de la Luna cuando ambos el Sol o la Luna están justamente comenzando a ser eclipsados o justamente [la Luna] ha completado la emersión (por ej. cuando los círculos son tangentes exteriormente). Unir AG, AD, AE.
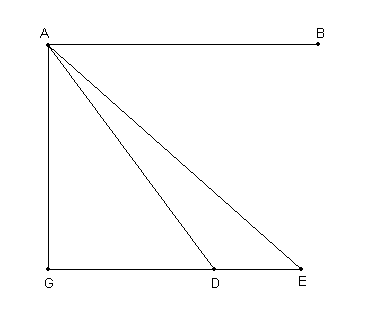
Es obvio que los ángulos BAG y AGE, que corresponden al tiempo del eclipse medio, a los sentidos están a ángulos rectos, y que el ^ BAE representa los ángulos al comienzo y al final del eclipse, mientras el ^ BAD representa los ángulos al final de [la fase parcial del] eclipse y al comienzo de la emersión. Y es inmediatamente claro que AE representa la suma del radio de ambos círculos, y AD su diferencia [9].
Luego tomamos como ejemplo un Eclipse Solar en el que la mitad del diámetro del Sol es oscurecido en el eclipse medio. Sea A el centro del Sol. Entonces, en todos los casos (dado que asumimos a la Luna en su distancia media) AE llega a [ser] [0;15,40º + 0;16,40º =] 0;32,20º, y AG, que es menor a este [valor] por la mitad del diámetro del Sol, llega a [ser de] 0;16,40º.
Por lo tanto, dado que AG = 16;40p donde la hipotenusa EA = 32;20p (de acuerdo con la magnitud de oscurecimiento asumido),
donde la hipotenusa AE = 120p
AG = 61;51p,
y, en el círculo alrededor del triángulo rectángulo AGE
arco AG = 62;2º.
En consecuencia ^ AEG = ^ BAE = 62;2ºº donde 2 ángulos rectos = 360ºº
en consecuencia ^ AEG = ^ BAE = 31;1º donde 4 ángulos rectos = 360º.
Nuevamente, tomamos el caso de un Eclipse Lunar, sea A el centro del cono sombra. Entonces, dado que, como antes, asumimos la Luna en su distancia media, AE siempre será la misma cantidad, a saber de [0;43,20º + 0;16,40º =] 60 minutos, y AD, igualmente, siempre será de [0;43,20º - 0;16,40º =] 26;40 minutos. Sea la Luna eclipsada en una situación tal que la magnitud [oscurecimiento] es de 18 dígitos. Por lo tanto AG es nuevamente menor que AD por la mitad del diámetro [de la luna] [10] y, por sustracción [de 16;40' desde 26;40'], AG llega a [ser de] 10;0 minutos.
Entonces, donde la hipotenusa AE = 120p, AG = 20;0p, y, en el círculo en el triángulo rectángulo AGE,
arco AG = 19;12º.
En consecuencia ^ AEG = ^ BAE = 19;12ºº donde 2 ángulos rectos = 360ºº
en consecuencia ^ AEG = ^ BAE = 9;36º donde 4 ángulos rectos = 360º.
Similarmente, donde la hipotenusa AD = 120p, AG = 45p, y, en el círculo en el triángulo rectángulo AGD,
arco AG = 44;2º.
En consecuencia ^ ADG = ^ BAD = 44;2ºº donde 2 ángulos rectos = 360ºº
en consecuencia ^ ADG = ^ BAD = 22;1º donde 4 ángulos rectos = 360º.
En el mismo sentido calculamos los tamaños de los ángulos para los otros dígitos [enteros de magnitud], [siempre tomando] aquel ángulo el cual fue menor que un ángulo recto, en unidades donde un ángulo recto es igual a 90º (correspondiente a la graduación del cuadrante del horizonte).

Construimos una tabla con 22 líneas y 4 columnas. La primer columna contiene los dígitos del oscurecimiento actual, medido a lo largo del diámetro, [y] hallado para el eclipse medio; la segunda contiene los ángulos ocurriendo en los eclipses solares en el momento del comienzo del eclipse y en el momento del fin de la emersión (egreso); la tercer columna contiene los ángulos ocurriendo en los eclipses lunares en los momentos del comienzo del eclipse y al final de la emersión; y la cuarta también contiene los ángulos ocurriendo en los eclipses lunares, en el momento del fin de [la fase parcial del] eclipse y en el momento del comienzo de la emersión. El diseño de la tabla y del círculo (diagrama Fig. 6.7) son los siguientes.
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Libro VI |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 | 11 | 12 |
| 13 |
Notas de referencia
- ↑ Sobre los capítulos 11 al 13 ver HAMA 141-4.
- ↑ O "direcciones", . Para otros usos de esta palabra ver el Libro I Capítulo 7 nota de referencia nro. 2 y el Libro V Capítulo 5 nota de referencia nro. 2. El propósito de calcular estos ángulos fue probablemente una predicción de tiempo (climático): ver HAMA II 999.
- ↑ Leer (en el manuscrito D y el Ar) en cambio de en H537, 12-13. Esto último podría significar "que coincide con el eclipse medio [para aquellos eclipses] en los cuales no hay una fase total". La interpolación sea probablemente el remanente de un leve intento para listar todos los casos posibles.
- ↑ La astronomía Griega algunas veces adopta el sentido popular para indicar los puntos del compás (brújula, ver Rosa de los Vientos) por los nombres de los vientos. Esto no ocurre en el Almagesto, excepto para y en el Libro VIII Capítulo 4 para designar las direcciones generales de "Este" y "Oeste", y en el diagrama Fig. 6.7, donde estos son una interpolación tardía en el manuscrito, no mencionada en el texto (ver abajo la nota de referencia nro. 7). Sobre los sistemas con nombres de los vientos (los cuáles verdaderamente varían) ver Albert Rehm, "Griechische Windrosen".
- ↑ Libro II Capítulo 2 Fig. 2.1.
- ↑ . Uno bastante podría esperar como , que esta implícito en la traducción de Ishaq.
- ↑ En las figuras de los manuscritos Griegos, esas designaciones están sobre el círculo más externo; por lo tanto Heiberg (en H539,7; cf. ibid. p. VI) enmendó , en la lectura de todos los manuscritos, por ("el más externo"). Aunque en la tradición Árabe ellos aparecen, en todo o en parte, sobre el círculo más interno, y parece como si ellos fueron transferidos al círculo más externo cuando los nombres de los vientos fueron adicionados (después de Ptolomeo) en el círculo más interno (cf. ver arriba la nota de referencia nro. 4).
Nota del traductor al español: tanto las leyendas "Salida Equinoccial" y la "Puesta Equinoccial" las escribí, en el centro, en ambas mitades de la línea del horizonte. Las leyendas "Salida Invernal", "Salida Vernal", "Puesta Invernal" y "Puesta Vernal" las escribí en el exterior del séptimo anillo circular encima del símbolo zodiacal correspondiente. - ↑ Sobre esta figura ver HAMA 38-9. Como Ptolomeo lo dibujó, esta es, como él dice, una representación esquemática de una tabla. Aunque encaja cercanamente a una representación en coordenadas polares. Si fuera verdaderamente tal, no obstante, todas las líneas rectas excepto las verticales y las horizontales podrían llegar a ser curvas (ver HAMA p. 1216 FIG. 32). He omitido los nombres de los vientos hallados en los manuscritos Griegos y en algunos Árabes, y en la figura de Heiberg. Cf. nota de referencia anterior nro. 7. La figura esta en el siguiente capítulo (Libro VI Capítulo 12 Fig. 6.7).
Corrección a Heiberg: para la latitud de Clima VI leer (en los manuscritos A y D, Is) en cambio de (45;34º). Corregido por Heiberg ad loc. - ↑ Cf. HAMA Fig. 124 p. 1244.
- ↑ Ver la Fig. M (copiada de la figura de Manitius en p. 409). Dado que el eclipse tiene una magnitud de 18 dígitos, por definición XY = 6 dígitos = radio de la Luna. Por lo tanto AX = AY - XY = radio del cono de sombra menos el radio de la Luna = AD. Por lo tanto AG = AX - XG = AD menos el radio de la Luna.
