Almagesto: Libro II - Capítulo 10
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
El tema restante en la presente teoría es la discusión de los ángulos formados en la Eclíptica. Primero debemos tener en claro que definiremos un ángulo entre [dos] grandes círculos de la siguiente manera: decimos que estos [dos] grandes círculos forman un ángulo recto cuando un círculo teniendo como polo la intersección de los grandes círculos y como radio, cualquier distancia que tenga [exactamente] un cuadrante interceptado entre los segmentos de los grandes círculos formando el ángulo; en general, cualquier proporción que el arco interceptado de un círculo descrito de la manera anterior tenga con respecto al círculo en su totalidad es la misma que la proporción del ángulo entre los planos [de los dos grandes círculos] con los cuatro ángulos rectos. Por lo tanto, dado que establecimos la circunferencia del círculo como de 360º, el ángulo subtendiendo el arco interceptado contendrá el mismo número de grados como el arco, en el sistema donde un ángulo recto contiene 90º.
A los propósitos de nuestra investigación presente, los ángulos más útiles en la Eclíptica son aquellos formados por
[1] la intersección de la Eclíptica y [con] el Meridiano,
[2] la intersección de la Eclíptica y el Horizonte para todas las posiciones [de la Eclíptica], y
[3] la intersección de la Eclíptica y un gran círculo dibujado a través de los polos del Horizonte [por ej. un círculo de altitud];
el proceso de encontrar esto último también dará origen al arco de este círculo [de altitud] cortado entre su intersección con la Eclíptica y el polo del horizonte, por ej. el Cenit. Los cálculos de cada uno de los ángulos de arriba, además de ser un tema más adecuado de la teoría propia, también juega una parte importante en los requerimientos de la Paralaje Lunar: es imposible hacer algún progreso en este tema sin haber comprendido primero como calcular estos ángulos.
Ahora hay cuatro ángulos en la intersección de los dos círculos (me refiero a la Eclíptica y a cualquiera de los círculos [de arriba] intersecándola). Dado que [siempre] discutiremos solamente uno de ellos, que ocupa siempre la misma posición relativa, debemos hacer la siguiente definición preliminar. En general, cuando demostramos en que continúa las características y los tamaños de un ángulo, nos referimos a aquel ángulo [de los cuatro posibles] que se ubica hacia atrás de la intersección de los círculos y hacia el Norte de la Eclíptica [2].
El cálculo de los ángulos entre el Meridiano y la Eclíptica es simple, entonces empezaremos con ello, y primero demostraremos que aquellos puntos sobre la Eclíptica equidistantes desde el mismo Equinoccio generan ángulos del tipo de arriba [descritos siendo] iguales unos con otros.
[Ver Fig. 2.9] Sea ABG un arco del Ecuador, DBE un arco de la Eclíptica, y Z el polo del Ecuador. Cortar arcos iguales, BH y BΘ, sobre lados opuestos del Equinoccio B, y dibujar a través del polo Z y de los puntos H y Θ los arcos del meridiano ZKH y ZΘL.

Y digo que
^ KHB = ^ ZΘE. [1]
[Demostración:] Esto es inmediatamente obvio. El triángulo esférico BHK tiene todos sus ángulos iguales a los ángulos del triángulo esférico BΘL, dado que los tres lados correspondientes en cada uno de los triángulos son iguales, HB con BΘ, HK con ΘL, y BK con BL. Todo esto ha sido previamente probado [3].
Por lo tanto ^ KHB = ^ BΘL = ^ ZΘE.
Lo que se ha requerido para examinar.
Segundo, debemos probar que la suma de los ángulos entre la Eclíptica y el Meridiano en los puntos sobre la Eclíptica equidistando del mismo solsticio, es igual a dos ángulos rectos.
[Ver Fig. 2.10.] Sea ABG un arco de la Eclíptica, con B tomado como Solsticio. Sean BD y BE arco iguales, tomados sobre los lados opuestos a él [B], y dibujar a través de Z el polo del Ecuador, y [desde] los puntos D y E los arcos meridianos ZD y ZE.
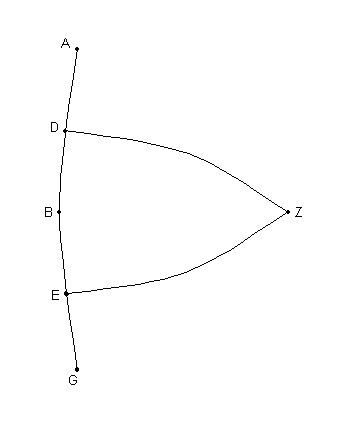
Y digo que
^ ZDB + ^ ZEG = 2 ángulos rectos. [2]
[Demostración:] También esto es inmediatamente obvio. Ya que los puntos D y E son equidistantes desde el mismo Solsticio,
arco DZ = arco ZE.
en consecuencia ^ ZDB = ^ ZEB.
Pero ^ ZEB + ^ ZEG = 2 ángulos rectos.
en consecuencia ^ ZDB + ^ ZEG = 2 ángulos rectos.
Lo que se ha requerido para examinar.
Habiendo establecido estos teoremas preliminares, dibujemos [Fig. 2.11] el círculo meridiano ABGD y el semicírculo de la Eclíptica AEG (tomando A como el Solsticio de invierno); luego, con el polo A y el radio del lado del cuadrado inscrito, dibujar el semicírculo BED. Entonces, ya que el Meridiano ABGD va a través de los polos de AEG y de los polos de BED, el arco ED es un cuadrante [4].

Por lo tanto ^ DAE es recto.
Y, según el teorema previo [2], el ángulo en el Solsticio de verano también es recto.
Lo que se ha requerido para examinar.
Nuevamente, [ver Fig. 2.12] sea ABGD un círculo meridiano, AEG un semicírculo del Ecuador, y AZG un semicírculo de la eclíptica en tal posición donde A es el equinoccio de otoño. Entonces con el polo A y el radio del lado del cuadrado [inscripto] dibujar el semicírculo BZED.

Por el mismo razonamiento [como el de arriba], dado que ABGD pasa a través de los polos de los [círculos] AEG y BED, AZ y ED son cuadrantes. Por lo tanto el punto Z es el Solsticio de invierno, y
arco ZE ≈ 23;51º, como fue demostrado previamente en el Libro I Capítulo 12.
Por lo tanto, por adición, el arco ZED = 113;51º
y ^ DAZ = 113;51º donde un ángulo recto = 90º.
Y nuevamente, del teorema previo [2], el ángulo de 66;9º es el suplemento en el punto del Equinoccio de primavera.
Nuevamente [ver Fig. 2.13] sea ABGD un círculo meridiano, AEG un semicírculo del Ecuador, y BZD un semicírculo de la eclíptica en tal posición que el punto Z es el equinoccio de otoño, y el arco BZ es (primero ante todo) la longitud de un signo, aquel de Virgo; por lo tanto el punto B, obviamente, es el comienzo de Virgo. Nuevamente, con el polo B y el radio del lado del cuadrado [inscripto], dibujar el semicírculo HΘEK.

Sea el problema encontrar ^ KBΘ.
Ahora, dado que el meridiano ABGD pasa a través de los polos de [los círculos] AEG y HEK, el arco BH, el arco BΘ y el arco EH son todos cuadrantes.
Y, de la figura,
| Cuerda arco 2 * BA / Cuerda arco 2 * AH = (Cuerda arco 2 * BZ / cuerda arco 2 * ΘZ) * (Cuerda arco 2 * ΘE / cuerda arco 2 * EH) [M.T.II] Configuración de Menelao |
Pero, como fue mostrado previamente [5],
arco 2 * BA = 23;20º, entonces Cuerda arco 2 * BA = 24;16p,
arco 2 * AH = 156;40º, entonces Cuerda arco 2 * AH = 117;31p,
y arco 2 * ZB = 60º, entonces Cuerda arco 2 * ZB = 60p,
arco 2 * ZΘ = 120º, entonces Cuerda arco 2 * ZΘ = 103;55,23p.
En consecuencia
| Cuerda arco 2 * ΘE / cuerda arco 2 * EH = (24;16 / 117;31) / (60 / 103;55,23) ≈ 42;58 / 120. |
Pero Cuerda arco 2 * EH = 120p.
en consecuencia Cuerda arco 2 * ΘE ≈ 42;58p.
en consecuencia arco 2 * ΘE ≈ 42º
y arco ΘE ≈ 21º [6].
Por lo tanto, por adición [de un cuadrante] el arco ΘEK = ^ KBΘ = 111º, y el ángulo en el principio de Scorpius es también de 111º, y los ángulos en el principio de Taurus y de Pisces son cada uno de 69º, el suplemento, dados por los teoremas arriba provistos [1] y [2].
Lo que se ha requerido para examinar.
Seguido, en la misma figura [2.13], sea ZB el arco que representa dos signos, entonces este punto B es el comienzo de Leo. Luego, [hacer] lo mismo con las [otras] cantidades restantes,
arco 2 * BA = [2 * δ (60º) =] 41º, entonces Cuerda arco 2 * BA = 42;2p
y arco 2 * AH = 139º, entonces Cuerda arco 2 * AH = 112;24p;
además arco 2 * ZB = 120º, entonces Cuerda arco 2 * ZB = 103;55,23p
y arco 2 * ZΘ = 60º, entonces Cuerda arco 2 * ZΘ = 60p.
Por lo tanto
| Cuerda arco 2 * ΘE / cuerda arco 2 * EH = (42;2 / 112;24) / (103;55,23 / 60) = 25;53 / 120. |
En consecuencia Cuerda arco 2 * ΘE = 25;53p
por lo tanto arco 2 * ΘE ≈ 25º
y arco ΘE ≈ 12 ½º [7].
Por lo tanto, por adición, el arco ΘEK = ^ KBΘ = 102 ½º.
Por lo tanto el ángulo en el comienzo de Sagittarius es también de 120 ½º, y el ángulo tanto en el comienzo de Gemini y como en el comienzo de Aquarius es el [ángulos] suplementario, de 77 ½º.
De este modo hemos calculado lo que nos propusimos hacer. Para su uso práctico es suficientemente visualizar [los resultados] para cada signo, aunque el mismo procedimiento se aplicaría inclusive a las secciones más pequeñas de la Eclíptica.
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Libro II |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 | 11 | 12 |
| 13 |
Notas de referencia
- ↑ Sobre los capítulos 10 y 11 ver HAMA 45-8, Pedersen 115-18.
- ↑ Literalmente “uno de los dos ángulos sobre el arco hacia atrás de la intersección de los círculos que esta al Norte de la Eclíptica”. Ver HAMA 45 en la Fig. 38.
- ↑ HB = BΘ por construcción, HK = ΘL, [son] las declinaciones de los puntos equidistantes desde un Equinoccio (cf. Libro II Capítulo 3 nota de referencia nro. 4); BK = BL, cf. Libro II Capítulo 7 (arco EΘ = arco EZ).
- ↑ Derivado de la obra “Esférica” de Teodosio, Libro II Capítulo 9.
- ↑ Referencia a Libro II Capítulo 7. Aquí las cantidades son redondeadas.
- ↑ Cálculos precisos podrían dar 20;58º al minuto más próximo.
- ↑ Cálculos precisos podrían dar 12;28º al minuto más próximo.
