Almagesto: Libro II - Capítulo 12
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
{Sobre los ángulos y arcos formados con el mismo Círculo [por ej. el de la Eclíptica cortado] por un Círculo dibujado a través de los Polos del Horizonte}
[1].
Resta [describir] el método por el cual podemos calcular los ángulos formados entre la Eclíptica y el Círculo a través de los Polos del Horizonte (por ej. un círculo de Altitud) para cualquier latitud y para cualquier posición relativa [de la Eclíptica al círculo de Altitud]. Como dijimos, este método también genera la longitud del arco del círculo a través de los polos del Horizonte cortado entre el Cenit y la intersección de este círculo con la Eclíptica. Nuevamente estableceremos también los teoremas preliminares para este tema: probaremos, primero, que si estos dos puntos de la Eclíptica son equidistantes desde el mismo Solsticio, y cortan con un número igual de grados de tiempo sobre ambos lados del meridiano, uno hacia el Este y el otro hacia el Oeste, por lo tanto los arcos del gran círculo desde el Cenit hasta aquellos dos puntos son iguales, y la suma de los [dos] ángulos en estos puntos, elegidos de acuerdo a nuestra [definición] previa [2], es igual a dos ángulos rectos.
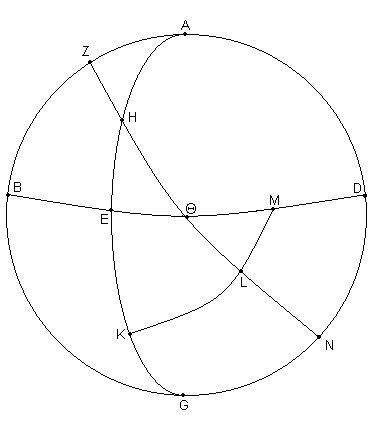
[Ver Fig. 2.18.]. Sea ABG un segmento del meridiano, con el punto B sobre él tomado como el cenit, y el punto G como el polo del Ecuador. Dibujar dos segmentos de la Eclíptica, ADE y AZH, tales que los puntos D y Z son equidistantes desde el mismo Solsticio, y cortados, sobre ambos lados del meridiano ABG, en arcos iguales del círculo paralelo que pasan a través de ellos. Además, dibujar a través de los puntos D y Z los siguientes arcos de gran círculo: el arco GD y el arco GZ desde el polo del Ecuador G, y el arco BD y el arco BZ desde el Cenit B.
Digo que
arco BD = arco BZ
y ^ BDE + ^ BZA = 2 ángulos rectos.
[Demostración:] Dado que los puntos D y Z cortan arcos iguales del círculo paralelo a través de ellos sobre ambos lados del meridiano ABG,
^ BGD = ^ BGZ.

Por lo tanto, en dos triángulos esféricos BGD, BGZ
GD = GZ [D y Z son equidistantes desde el Solsticio]
BG = BG (en común)
y ^ BGD = ^ BGZ,
entonces ellos tienen dos lados y el ángulo incluido [comprendido] igual.
En consecuencia BD = BZ (las bases de cada ∆ esférico)
y ^ BZG = ^ BDG.
Pero de lo demostrado justamente arriba de que la suma de dos ángulos, formados por un círculo que pasa a través de los polos del Ecuador en los puntos [de la Eclíptica] que equidistan del mismo Solsticio, es igual a dos ángulos rectos [10.2],
^ GDE + ^ GZA = 2 ángulos rectos.
Pero probamos que
^ BDG = ^ BZG.
Por lo tanto ^ BDE + ^ BZA = 2 ángulos rectos [3].
Lo que se ha requerido para examinar.
Seguidamente debemos probar que si tomamos el mismo punto de la Eclíptica en dos posiciones equidistantes desde el meridiano (medido en grados de tiempo) sobre lados opuestos a él, los arcos del gran círculo desde el Cenit hasta esas dos posiciones son iguales, y la suma de los dos ángulos Este y Oeste [del meridiano, entre el círculo de Altitud y la Eclíptica], es igual al doble del ángulo formado por el mismo punto [de la Eclíptica] sobre el meridiano, dado esto para ambas posiciones [por ej. cuando el punto esta al Este y al Oeste del meridiano] los puntos [de la Eclíptica] que están [entonces] culminando están ambos al Norte o ambos al Sur del Cenit.
Supongamos, primero, que ambos están al Sur. [ver Fig. 2.19.]. Sea ABGD el segmento del meridiano, con el punto G sobre él como Cenit, y D como el polo del Ecuador. Dibujar dos segmentos de la Eclíptica, AEZ y BHΘ, tal que los puntos E y H representan el mismo punto, y corta arcos iguales del círculo paralelo [que pasan] a través de ese punto sobre los lados opuestos del meridiano ABGD. Nuevamente, dibujar a través de ellos [de los puntos E y H] los arcos GE y GH de un gran círculo desde G, y DE y DH desde D. Por el mismo razonamiento según lo anterior, dado que los puntos E y H generan el mismo círculo paralelo y cortan arcos iguales de él a ambos lados del meridiano,

∆ esférico GDE ≡ ∆ esférico GDH.
En consecuencia arco GE = arco GH.
Luego digo que
^ GEZ + ^ GHB = 2 ^ DEZ = 2 ^ DHB.
[Demostración:] dado que ^ DEZ es el mismo que ^ DHB [E y H son el mismo punto]
y ^ GED = ^ DHG [desde ∆ esféricos congruentes],
^ GED + ^ GHB [= ^ DHG + ^ GHB = ^ DHB] = ^ DEZ.
Por lo tanto,
por adición ^ GEZ + ^ GHB = 2 ^ DEZ = 2 ^ DHB
Lo que se ha requerido para examinar.
Seguidamente, dibujar nuevamente los mismos segmentos de los círculos de arriba [Fig. 2.20], excepto que aquellos puntos A y B deberían estar al Norte del punto G. Digo que aquí también lo mismo será aplicado, a saber
^ KEZ + ^ LHB = 2 ^ DEZ.
[Demostración:] Dado que el ^ DEZ es el mismo que el ^ DHB,
y ^ DEK = ^ DHL [son suplementos de los ángulos iguales DEG y DHG],
por adición [del ^ DHB al ^ DHL], ^ LHB = ^ DEZ + ^ DEK.
Por lo tanto ^ LHB + ^ KEZ = 2 ^ DEZ.
Nuevamente dibujar ahora [Fig. 2.21.] una figura similar [a la 2.20], excepto que el punto de culminación sobre el segmento [de la Eclíptica] al Este [del meridiano], a saber [el punto] A, debería estar al Sur del Cenit G, mientras el punto de culminación sobre el segmento al Oeste [del meridiano], a saber B, debería estar al Norte del Cenit.


Digo que
^ GEZ + ^ LHB = 2 ^ DEZ más 2 ángulos rectos.
[Demostración:] Dado que
^ DHG = ^ DEG
y ^ DHG + ^ DHL = 2 ángulos rectos,
en consecuencia ^ DEG + ^ DHL = 2 ángulos rectos.
Pero ^ DEZ es el mismo como el ^ DHB.
Por lo tanto ^ GEZ + ^ LHB [= (^ DEZ + ^ DEG) + (^ DHB + ^ DHL)]
= (^ DEZ + ^ DHB) + (^ DEG + ^ DHL)
= (^ DEZ + ^ DHB) más 2 ángulos rectos
= 2 ^ DEZ más 2 ángulos rectos.
Lo que se ha requerido para examinar.
Para el caso restante, dibujar una figura [Fig. 2.22] similar [a la anterior], en la cual el punto A, que esta culminando en la sección Este [del meridiano], esta al Norte de G, mientras [que] B, que esta culminando en la sección Oeste [del meridiano], esta al Sur del [Cenit].

Y digo que
^ KEZ + ^ GHB = 2 ^ DEZ menos 2 ángulos rectos.
[Demostración:] Por el mismo razonamiento anterior
^ KEZ + ^ GHB = (^ DEZ + ^ DHB) – (^ DEK + ^ DHG)
= 2 ^ DEZ – (^ DEK + ^ DHG).
Pero ^ DEK + ^ DHG = 2 ángulos rectos, ya que
^ DEK + ^ DEG = 2 ángulos rectos, y ^ DEG = ^ DHG.
Lo que se ha requerido para examinar.
De los ángulos y arcos formados en el trayecto definido entre la Eclíptica y un círculo de Altitud, aquellos en el meridiano y en el Horizonte, inmediatamente pueden ser fácilmente calculados tal como puede ser visto del siguiente modo.
Dibujar [Fig. 2.23] el círculo meridiano ABGD, el semicírculo del horizonte BED, y el semicírculo ZEH de la Eclíptica en cualquier posición. Luego si imaginamos el círculo de Altitud a través del Cenit A y Z el punto culminante de la Eclíptica, este coincide con el meridiano ABGD, y el ^ DZE será inmediatamente dado, ya que son dados [4] el punto Z y el ángulo que [la Eclíptica hace] con el meridiano en el punto Z. El arco AZ será también dado, ya que conocemos la distancia en grados del punto Z desde el Ecuador (medida a lo largo del meridiano), y la distancia del Ecuador desde el Cenit A [5].

Seguidamente, si imaginamos el círculo de altitud AEG, dibujar a través del punto E en la salida de la Eclíptica, y [del Cenit] A, aquí también es inmediatamente obvio que el arco AE es siempre un cuadrante, dado que el punto A es el polo del Horizonte BED. Por la misma razón, el ^ AED es siempre recto; y dado que el ángulo que la Eclíptica hace con el Horizonte esta dado [6], a saber el ^ DEH, la suma [resultante, es decir] el ángulo AEH, será dado también.
Lo que se ha requerido para examinar.
Por lo tanto esta claro que, dado que se mantienen las proporciones descritas anteriormente, si calculamos, justamente los ángulos y los arcos anteriores [por ej. al Este del] meridiano, y justamente para los signos desde el comienzo de Cancer hasta el principio de Capricornus, también habremos encontrado simultáneamente los ángulos y los arcos para los mismos signos [desde Cancer hasta Capricornus] después del meridiano, y también los ángulos y los arcos ambos antes y después del meridiano para los signos restantes.
Pero en orden de hacer claro el procedimiento, también en este caso para alguna posición [de la Eclíptica], visualizaremos como ejemplo el método general por medio de una simple solución al problema [7]. En la misma latitud, a saber, donde la Altura [la elevación] del polo Norte desde el Horizonte es de 36º (Rodas), supongamos que el comienzo de Cancer está, por ej. a una hora equinoccial hacia el Este del meridiano. En esta situación, en la latitud de arriba, el [punto de la Eclíptica] ♊︎ 16;12º esta culminando, y el [punto] ♍︎ 17;37° esta saliendo.
Entonces [Fig. 2.24.] sea ABGD el círculo meridiano, BED el semicírculo del horizonte, y ZHΘ el semicírculo de la Eclíptica en tal posición que el punto H esta en el comienzo de Cancer, mientras Z representa ♊︎ 16;12º y Θ ♍︎ 17;37º. Dibujar el Cenit a través de A, y por H, el comienzo de Cancer, el segmento AHEG del gran círculo [de altitud]. Sea el primer problema hallar el arco AH.

Ahora es claro que
arco ZΘ = 91;25º [ ♍︎ 17;37º - ♊︎ 16;12º ]
y arco HΘ = 77;37º [ ♍︎ 17;37º - ♋︎ 0º ].
Similarmente, dado que ♊︎ 16;12º corta 23;7º del meridiano al Norte del Ecuador, y el Ecuador corta 36º [del meridiano] desde el Cenit A,
y arco AZ = 12;53º
y arco ZB = 77;7º (su [arco] complementario).
Cuando son dadas estas cantidades, desde la figura
| Cuerda arco 2 * ZB / cuerda arco 2 * BA = (cuerda arco 2 * ZΘ / cuerda arco 2 * ΘH) * (cuerda arco 2 * HE / cuerda arco 2 * EA). [M.T.I.] Configuración de Menelao. |
Pero arco 2 * ZB = 154;14º, entonces Cuerda arco 2 * ZB = 116;59p
y arco 2 * BA = 180º, entonces Cuerda arco 2 * BA = 120p.
Además arco 2 * ZΘ = 182;50º, entonces Cuerda arco 2 * ZΘ = 119;58p
y entonces arco 2 * ΘH = 155;14º, entonces Cuerda arco 2 * ΘH = 117;12p.
Por lo tanto
| Cuerda arco 2 * EH / Cuerda arco 2 * EA = (116;59 / 120) / (119;58 / 117;12) ≈ 114;16 / 120. |
Pero Cuerda arco 2 * EA = 120p
en consecuencia Cuerda arco 2 * EH = 114;16p
por lo tanto arco 2 * EH ≈ 144;26º
y arco EH = 72;13º.
En consecuencia arco AH = 17;47º (su [arco] complementario).
Lo que se ha requerido para examinar.
Seguidamente encontraremos el ^ AHΘ, tal como sigue.
Dibujar la misma figura [Fig. 2.25], y con el polo H y el radio del lado del cuadrado [inscripto] dibujar el segmento KLM del gran círculo.
Entonces, dado que el círculo AHE esta dibujado a través de los polos de EΘM y KLM, ambos EM y KM son cuadrantes. Nuevamente, de la figura
| Cuerda arco 2 * HE / Cuerda arco 2 * EK = (Cuerda arco 2 * HΘ / Cuerda arco 2 * ΘL) * (Cuerda arco 2 * LM / Cuerda arco 2 * KM). [M.T.II.] Configuración de Menelao. |
Pero arco 2 * HE = 144;26º [según arriba], entonces Cuerda arco 2 * HE = 114;16p
y arco 2 * EK = 35;34º, entonces Cuerda arco 2 * EK = 36;38p.
Además arco 2 * ΘH = 155;14º, entonces Cuerda arco 2 * ΘH = 117;12p
y arco 2 * ΘL = 24;46º, entonces Cuerda arco 2 * ΘL = 25;44p.
En consecuencia
| Cuerda arco 2 * LM / Cuerda arco 2 * MK = (114;16 / 36;38) / (117;12 / 25;44) ≈ 82;11 / 120. |
Pero Cuerda arco 2 * MK = 120p
en consecuencia Cuerda arco 2 * LM = 82;11p
por lo tanto arco 2 * LM = 86;28º
y arco LM = 43;14º.
En consecuencia arco LK = ^ LHK = 46;46º (su [arco] complementario).
Por lo tanto ^ AHΘ = 133;14º (su [ángulo] suplementario).
Lo que se ha requerido para examinar.
El mismo método que fue utilizado para hallar lo de arriba, también se aplica a los [arcos y ángulos] restantes. Pero con el fin de tener convenientemente visualizado todos los otros arcos y ángulos, por lo que es razonable suponer que podemos necesitarlo en nuestras investigaciones particulares, también calculamos geométricamente estos, comenzando desde el paralelo a través de Meroe, en el cual el día más largo es de 13 Horas Equinocciales, y subiendo hasta el paralelo por encima del Ponto (Mar Negro), [que pasa] a través de las bocas del Borysthenes, donde el día más largo es de 16 horas Equinocciales [8]. Los intervalos que utilizamos fueron de la mitad de una hora [de longitud del día más largo] entre los paralelos de latitud (como para los tiempos de Salida), un signo para las secciones de la Eclíptica, y una Hora Equinoccial para la posición [de los círculos de altitud] hacia el Este y hacia el Oeste del meridiano.
Visualizaremos los resultados en forma tabular, un conjunto de tablas para cada paralelo de latitud, y una tabla para cada signo. Primero, en la primera columna colocamos, la ubicación del meridiano [en cuestión], luego la distancia antes y después del meridiano, medida en horas equinocciales. En la segunda columna colocamos la cantidad del arco correspondiente (como lo explicado arriba) desde el Cenit hasta el comienzo del signo en cuestión. En la tercera y la cuarta columna colocamos la cantidad de los ángulos formados por la intersección, arriba mencionada, [entre la Eclíptica y el círculo de Altitud], definida por el camino que explicamos: los ángulos en las posiciones hacia el Este del meridiano en la tercera columna, y aquellos en las posiciones hacia el Oeste del meridiano en la cuarta columna. Uno debe mantener en mente que, de acuerdo con nuestra definición original [9], siempre tomamos el ángulo que se ubica hacia atrás de la intersección de los círculos y hacia el Norte de la eclíptica, y su magnitud expresada en el sistema en el que un ángulo recto es de 90 [grados]. El diseño de las tablas es el siguiente:
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Libro II |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 | 11 | 12 |
| 13 |
Notas de referencia
- ↑ Ver HAMA 48-52, Pedersen 118-21 (con mi corrección en Toomer [3] 139).
- ↑ Libro II Capítulo 10 en nota de referencia nro. 2.
- ↑ Para el ^ BDE = ^ GDE + ^ BDG; ^ BZA = ^ GZA - ^ BZG. Entonces, por adición (dado que ^ BDG = ^ BZG), ^ BDE + ^ BZA = ^ GDE + ^ GZA = 2 ángulos rectos.
- ↑ En Libro II Capítulo 10 (Fig. 2.13).
- ↑ δ y φ respectivamente, entonces el arco AZ = φ – δ.
- ↑ En Libro II Capítulo 11 (Fig. 2.17).
- ↑ Este ejemplo esta trabajado en HAMA a lo largo de 49-50.
- ↑ Los siete paralelos seleccionados aquí son de hecho las “7 clímatas” canónicas, por ellas ver la Introducción.
- ↑ Libro II Capítulo 10 en nota de referencia nro. 2.
