Almagesto: Libro I - Capítulo 12
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
{Sobre el arco entre los Solsticios}
Ahora que hemos tabulado las cuerdas, nuestra primera tarea, como dijimos, es determinar la inclinación de la Eclíptica con el Ecuador, es decir, la proporción del gran círculo a través de los polos de ambos con el arco interceptado entre los polos. Es obvio que esta es igual a la distancia desde el Ecuador hasta cualquiera de los puntos Solsticiales. Esta cantidad puede ser determinada directamente por un método instrumental, utilizando el siguiente aparato sencillo [2] [Ver Fig. C.].
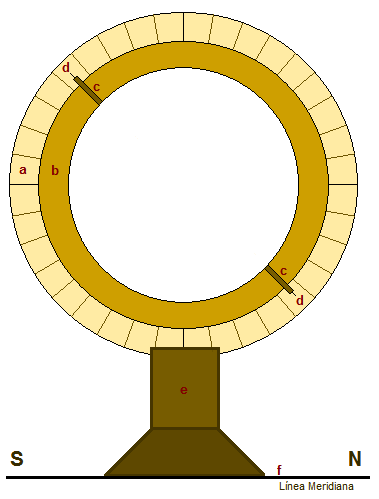
Construimos un aro de bronce (a) de un tamaño adecuado, lo giramos en torno para que su superficie este exactamente en escuadra [por ej. teniendo una sección transversal rectangular [(base)]. Lo utilizamos como círculo meridiano (ver el actual círculo meridiano), dividiéndolo en 360º de un gran círculo, y subdividiendo cada grado dentro de varias partes como [el tamaño del instrumento] lo permita. Luego tomamos otro aro pequeño (b), y lo ajustamos dentro del primero de tal manera que las caras laterales de ambos estén sobre el mismo plano, mientras el aro más pequeño pueda girar dentro del más grande, con un movimiento Norte-Sur, [siempre] sobre el mismo plano. En los dos puntos diametralmente opuestos sobre una de las caras laterales del aro más pequeño fijamos [dos] pequeñas planchuelas (c), de igual tamaño, apuntando cada una y hacia el centro de los aros, y exactamente en el medio de la longitud de cada planchuela fijamos unos pequeños punteros (d), que rozan la superficie del aro más grande graduado. Para servir a todos los propósitos necesarios fijamos este aro firmemente sobre un pilar (e) de tamaño apropiado, y lo ubicamos en un lugar abierto, tanto que la base del pilar este sobre una explanada que no este inclinada al plano del Horizonte. Tendremos cuidado de que el plano [lateral] de los aros sea perpendicular al plano del horizonte y paralelo al plano del Meridiano (f). Lo primero de esto [deseado], es tratar de suspender una línea a plomo (perpendicular) desde un punto [sobre el aro externo] elegido como Cenit, y ajustando los elementos de soporte [3] hasta que la línea de plomo apunte hacia el [otro] punto diametralmente opuesto [al punto del Cenit]. Lo segundo [por hacer] es conseguir marcar la línea meridiana [4] (f) tan claramente en el plano por debajo del pilar y moviendo los aros lateralmente hasta que uno pueda ver su plano [lateral] paralelo a aquella línea [meridiana]. [Ya] habiendo ubicado el instrumento de este modo, observamos el movimiento del Sol hacia el Norte y hacia el Sur girando el aro interno hasta que la planchuela de abajo este completamente bajo la sombra de la [planchuela] de arriba. Cuando este sea el caso, los extremos de los punteros nos indican la distancia del Sol desde el Cenit en grados [5], medidos a lo largo del meridiano.

Encontramos incluso una manera más práctica de hacer estas clases de observaciones construyendo, en cambio de los aros, una plaqueta (a) [ver Fig. D] de piedra o madera, cuadrada y rígida, con una de sus caras lisas y escuadrada en forma precisa. Sobre esta [cara] dibujamos un cuadrante (b), utilizando como centro un punto cerca de una de las esquinas, y dibujar desde el centro hacia el arco inscrito las líneas que entran en un ángulo recto formando el cuadrante. Dividimos el arco (c), como lo hicimos [con el otro instrumento], dentro de 90 grados y las subdivisiones de esos grados. Seguido, sobre esa línea que hemos elegido ser perpendicular al plano del horizonte y hacia el Sur, fijamos dos pequeñas clavijas cilíndricas (d), con sus lados en ángulo recto a sus bases y exactamente circulares, trabajadas siendo de igual tamaño: una de ellas esta fijada en el punto central propiamente dicho, posicionando el punto medio de la clavija precisamente sobre él, y la otra por debajo al final de la línea. Luego situamos la cara graduada de la placa a lo largo de la línea meridiana (g) que hemos dibujado sobre el plano de la base, siendo [la cara graduada] paralela al plano meridiano, y, utilizando una línea a plomo (e) suspendida entre las clavijas, establecemos la línea entre ellas, precisamente a ángulos rectos al plano del horizonte, nuevamente corrigiendo alguna deficiencia ajustando elementos de soporte delgados debajo. Del mismo modo como [hicimos] antes, observamos la sombra proyectada (f) al mediodía por la clavija [que está] en el centro [(vértice del ángulo recto)]. En orden de determinar su posición más precisamente, emplazamos algún objeto sobre el arco inscrito [por donde cruza la sombra]. Marcando el punto medio de la sombra, tomamos esta división del cuadrante indicando la posición del Sol en el meridiano (h) en dirección Norte-Sur [6].
Desde las observaciones de este tipo, y específicamente desde las observaciones comparadas cerca de los solsticios actuales, las cuales revelan que, sobre un número de vueltas [del Sol], la distancia desde el cenit es en general, el mismo número de grados del círculo meridiano sobre el [mismo] solsticio, siendo el de verano o el de invierno, hallamos que el arco entre el punto más al Norte y el punto más al Sur, que es el arco entre los puntos solsticiales, es siempre mayor que 47 ⅔º y menor que 47 3/4º. De esto derivamos en buena medida el mismo valor tal como el de Eratóstenes, que también utilizó Hiparco. [De acuerdo a esto] el arco entre los solsticios es aproximadamente 11 partes donde el meridiano es de 83 [7].
De los tipos de observaciones precedentes, inmediatamente es fácil derivar la latitud de la región en la cual la observación es realizada, por donde fuera que sea: uno toma el punto medio entre los dos extremos; este punto se ubica en el Ecuador; luego uno toma la distancia entre este punto y el Cenit, que es el mismo, obviamente, como la distancia de los polos desde el horizonte.
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Libro I |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 | 11 | 12 |
| 13 | 14 | 15 |
| 16 |
Notas de referencia
- ↑ Ver Britton [2] para la determinación de la oblicuidad de la eclíptica [realizada] por Ptolomeo.
- ↑ Sobre los instrumentos descritos aquí por Ptolomeo ver Price, “Precision Instruments”, 587-9. Hay una descripción detallada muy antigua sobre la construcción y uso de este aro (instrumento) por parte de Proclo, “Hypotyposis” III 5-27 (ed. Manitius pp. 42-52).
- ↑ Leer (en el manuscrito D) en cambio de en H65,13. Cf. H67,7. Ambas lecturas se encuentran en los manuscritos de Proclo, “Hypotyposis” p. 50,10.
- ↑ Ptolomeo asume que uno puede dibujar la línea meridiana, sin explicar cómo. Diodorus de Alejandría (primera centuria a. C.) en su tratado “Analema”, da un método ingenioso para determinar la línea meridiana desde alguna de las tres sombras del Gnomon (ver HAMA II 841-2). Ver: Trazado de la línea meridiana.
- ↑ , literalmente “divisiones”, y aquí puede ser interpretado [como] (“divisiones del arco graduado”), cf. p. 61. Pero en el Almagesto hay muchos lugares donde esto significa simplemente “grados”.
- ↑ , literalmente “en latitud”. Ptolomeo, siguiendo el uso del griego común, utiliza para alguna dirección “vertical”, incluyendo el Ecuador, como [lo hace] aquí. Ver Introducción.
- ↑ 11/83 de 360º ≈ 47;42,39,2º = 2ε, por lo tanto ε ≈ 23;51,20º, que es el [valor] que Ptolomeo adopta actualmente (su 2ε se ubica entre 47;40º y 47;45º, aunque este no es el valor medio).
El texto podría igualmente decir, ni que Eratóstenes ni Hiparco utilizaron la proporción de 11/83, aunque esta proporción de 11/83 es el valor de Ptolomeo, que es la más cercana a la proporción actual utilizada por ellos [a saber 2/15, por ej. ε = 24º]. Esta interpretación tiene una ventaja de acuerdo con el único valor por otro lado declarado por Eratóstenes (en su “Geografía”, ver Berger Frg. II B 23, Estrabón 2.5.7) e Hiparco (en su “Geografía” y en su “Comentario sobre Arato”, ed. Manitius p. 96,20; cf. HAMA 303, 335). Esto fue propuesto por Berger, “Eratóstenes” 131, seguido por Heath, “Aristarco” 131 n. 4. Prefiero la interpretación tradicional, dado que encuentro inconcebible que Ptolomeo no menciona que su proporción fuera la más acertada, y también por su expresión en el Libro I Capítulo 14. La proporción peculiar de Eratóstenes no es debida a una mala división del círculo dentro 83 partes, como Teón supuso (Rome II 529), sino por una derivación pre-trigonométrica de las mediciones de un gnomon, como demostraré en otra parte.
