Almagesto: Libro I - Capítulo 10
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
{Sobre la longitud (tamaño) de las Cuerdas}
Luego, para comodidad del lector, expondremos subsecuentemente una tabla con sus cantidades, dividiendo la circunferencia en 360 partes, y tabulando las cuerdas subtendidas por los arcos a intervalos de medio grado, expresando cada una como un número de partes en un sistema donde el diámetro [(de tal circunferencia)] esta dividido dentro de 120 partes. [Adoptaremos esta norma] por su conveniencia aritmética [2], que se harán evidentes a partir de los presentes cálculos. Pero primero, demostraremos cómo uno puede encargarse de los cálculos con sus cantidades por medio de un método rápido y simple, en lo posible utilizando algunos teoremas, el mismo conjunto para todo. Hacemos esto para que podamos no solo tener las cantidades de las cuerdas tabuladas sin chequear, sino también poder verificarlas fácilmente calculándolas por un estricto método geométrico. En general utilizaremos el sistema sexagesimal para nuestros cálculos aritméticos, debido a la dificultad del sistema fraccionario [convencional]. Dado que siempre apuntamos hacia una buena aproximación, solamente manejaremos multiplicaciones y divisiones solo en cuanto para alcanzar un resultado que difiera de la precisión lograda por los sentidos por una cantidad insignificante.
Primero, entonces, [ver Fig. 1.1] sea aquí un semicírculo ABG alrededor del centro D y con un diámetro ADG. Dibujemos la perpendicular DB hasta AG en D. Donde DG es bisecada [dividida en dos] en E, unir EB, y hacer EZ igual a EB. Unir ZB.

Digo que ZD es el lado del decágono [regular], y BZ el lado del pentágono [regular].
[Demostración:] Dado que la línea recta DG es bisecada [dividida en dos] en E, y una línea recta DZ es adyacente a ella,
GZ * ZD + ED² = EZ² [3].
pero EZ² = BE² (EB = ZE),
y EB² = ED² + DB².
por consiguiente GZ * ZD + ED² = ED² + DB².
por lo tanto GZ * ZD = DB² (Substrayendo ED², generalmente).
por consiguiente GZ * ZD = DG²
Entonces ZG ha sido cortada en proporción extrema y media en D [4].
Ahora dado que el lado del hexágono y el lado del decágono, cuando ambos están inscriptos en un mismo círculo, forman la proporción extrema y media de la misma línea recta [5], y dado que GD, siendo un radio, representa el lado del hexágono [6], DZ es igual al lado del decágono.
Similarmente, dado que el cuadrado del lado del pentágono es igual a la suma de los cuadrados de los lados del hexágono y del decágono cuando todos están inscriptos en el mismo círculo [7], y, en el triángulo rectángulo BDZ, el cuadrado de BZ es igual a la suma de los cuadrados en BD, que es el lado del hexágono, y en DZ, que es el lado del decágono, se deduce que BZ es igual al lado del pentágono.
Luego, ya que, como he dicho, establecimos el diámetro del círculo como de 120 partes, se deduce de lo de arriba [expresado] que:
DE = 30p (DE mitad del radio)
y DE² = 900p
BD = 60p (BD un radio)
y BD² = 3600p.
Y EZ² = EB² = 4500p, la suma [de DE² y BD²]
por consiguiente EZ ≈ 67;4,55p
Y por sustracción [de DE desde EZ], DZ = 37;4,55p. Entonces el lado del decágono, que subtiende 36º, tiene 37;4,55p donde el diámetro tiene 120p.
Nuevamente, dado que DZ = 37;4,55p,
DZ² = 1375;4,15p; [8]
y DB² = 3600p,
entonces BZ² = DZ² + DB² = 4975;4,15p.
por consiguiente BZ ≈ 70;32,3p
Por lo tanto el lado del pentágono, que subtiende 72º, contiene 70;32,3p donde el diámetro tiene 120p.
Inmediatamente es obvio que el lado del hexágono [inscrito], que subtiende 60º y es igual al radio, contiene 60p.
Similarmente, dado que el lado del cuadrado [inscrito], el cual subtiende 90º, es igual, cuando esta al cuadrado, al doble del cuadrado del radio, y dado que el lado del triángulo [inscrito], que subtiende 120º, es igual, cuando esta al cuadrado, a tres veces el cuadrado del radio, y el cuadrado del radio es de 3600p, calculamos que
el cuadrado en el lado del cuadrado, es de 7200p
y el cuadrado en el lado del triángulo es de 10800p.
por consiguiente Cuerda 90º ≈ 84;51,10p (*)
Cuerda 120º ≈ 103;55,23p (**)
(*) y (**) donde el diámetro es de 120p.
Luego podemos considerar las cuerdas de arriba como establecidas individualmente por los procedimientos directos anteriores.
Será inmediatamente [9] obvio si cualquier cuerda es dada, la cuerda del arco suplementario es dada de una manera sencilla, dado que la suma de sus cuadrados es igual al cuadrado del diámetro. Por ejemplo, dado que la cuerda de 36º fue demostrada ser de 37;4,55p, y el cuadrado de este es de 1375;4,15p, y el cuadrado del diámetro es 14400p, el cuadrado de la cuerda del arco suplementario (que es de 144º) será la diferencia, a saber de 13024;55,45p, y entonces
Cuerda 144º ≈ 114;7;37p.
Similarmente para las otras dos cuerdas [de los suplementarios].
Seguidamente demostraremos, como las cuerdas individuales restantes pueden ser derivadas desde las [cuerdas] arriba [expresadas], primero de todo se expondrá un teorema que es extremadamente útil para el asunto en cuestión.
[Ver Fig. 1.2.] Sea aquí un círculo con un cuadrilátero arbitrario ABGD, inscripto en él. Unir AG y BD.

Debemos probar que
AG * BD = AB * DG + AD * BG [10].
[Demostración:] Hacer ^ ABE = ^ DBG.
Luego, si agregamos el ^ en común EBD
^ ABD = ^ EBG.
Pero, ^ BDA = ^ BGE dado que ellos, también, subtienden el mismo segmento.
por consiguiente ∆ ABD ||| ∆ BGE.
por lo tanto BG / GE = BD / DA.
por consiguiente BG * AD = BD * GE.
Nuevamente, ya que ^ ABE = ^ DBG,
y ^ BAE = ^ BDG,
∆ ABE ||| ∆ BGD.
por lo tanto BA / AE = BD / DG.
por consiguiente BA * DG = BD * AE.
Pero fue demostrado que
BG * AD = BD * GE.
Por lo tanto, por adición,
AG * BD = AB * DG + AD * BG, [(según el Teorema de Ptolomeo)].
Lo que se ha requerido para examinar.
Habiendo establecido este teorema preliminar, dibujamos el semicírculo ABGD [Fig. 1.3], sobre el diámetro AD, y dibujamos desde A dos cuerdas, AB y AG, cada una dada en longitud en términos de un diámetro de 120p. Unir BG.
Digo que BG también es dada.
[Demostración:] Unir BD, GD.

Luego, claramente, BD y GD también serán dados, dado que ellas son cuerdas de [arcos] suplementarios [de los arcos de las cuerdas dadas, AB y AG].
Ahora, ABGD es un cuadrilátero cíclico,
AB * GD + AD * BG = AG * BD.
Pero AG * BD y AB * GD están dados.
por consiguiente AD * BG esta dado por sustracción.
Y AD es un diámetro.
Por lo tanto la cuerda BG es dada.
Y hemos demostrado que, si son dados dos arcos y las correspondientes cuerdas, la cuerda de la diferencia entre los dos arcos también será dada.
Es obvio que por medio de este teorema, estaremos listos para entrar [en la tabla] con un buen número de cuerdas, derivadas de la diferencia entre las cuerdas calculadas individualmente, y notablemente con la cuerda de 12º, ya que tenemos aquellas de 60º y de 72º.
Consideremos ahora el problema de encontrar la cuerda del arco que es la mitad de alguna cuerda dada [11].
Sea [Fig. 1.4.] ABG un semicírculo con diámetro AG. Sea GB una cuerda dada. Bisecar [dividir en dos] el arco GB en D, unir AB, AD, BD, DG, y eliminar la perpendicular DZ desde D hacia AG.

Y digo que
ZG = ½ * (AG – AB).
[Demostración:] Sea AE = AB, y unir DE.
Luego dado que [en los triángulos ABD, ADE]
AB = AE, y en común AD,
los dos pares de lados AB, AD y AE, AD son iguales.
Además ^ BAD = ^ EAD.
por consiguiente Base BD = Base DE.
pero BD = DG [por construcción]
por lo tanto DG = DE.
Entonces, ya que, en el triángulo isósceles DEG, la perpendicular DZ ha sido dibujada desde el ápex [(ápice, vértice)] hasta la base
EZ = ZG.
Pero EG = [AG – AE =] AG – AB.
por consiguiente ZG = ½ * (AG – AB).
Ahora, si la cuerda del arco BG es dada, la cuerda suplementaria AB es [también] inmediatamente dada.
Por lo tanto ZG, que es ½ * (AG – AB), es también dada. Pero, dado que, en el triángulo rectángulo AGD, la perpendicular DZ ha sido dibujada,
∆ ADG ||| ∆ DGZ (ambos ^ rectos) [12]
por consiguiente AG / GD = GD / GZ.
por lo tanto AG * GZ = GD².
pero AG * GZ esta dado
Por lo tanto GD² es dado, y entonces es también dada la cuerda GD, que subtiende un arco mitad [del arco de la cuerda dada] BG, que también es dado.
También, por medio de este teorema un gran número de cuerdas serán derivadas por la división [de los arcos de] las cuerdas previamente determinadas, y notablemente, desde la cuerda de 12º, desde las cuerdas de 6º, 3º, 1 ½º y ¾º. Por cálculo hallamos que la cuerda de 1 ½º es aproximadamente de 1;34;15p donde el diámetro es de 120p, y la cuerda de ¾º es aproximadamente de 0;47,8p en las mismas unidades.
Nuevamente, sea aquí [ver Fig. 1.5.] un círculo ABGD en el diámetro AD, con centro en Z. Desde A sean cortados sucesivamente dos arcos dados, AB, BG. Unir la cuerda correspondiente AB, BG; [que] también serán dadas.
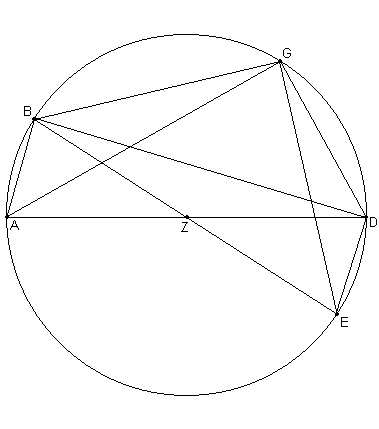
Digo, que si unimos AG, esta [cuerda] también será dada.
[Demostración:] dibujar a través de B el diámetro BZE, y unir BD, DG, GE, DE. Inmediatamente es claro que desde BG uno puede derivar GE, y desde AB uno puede derivar BD y DE [todas como cuerdas del arco suplementario]. Por un argumento similar al precedente [Fig. 1.3], dado que BGDE es un cuadrilátero cíclico [inscripto en el círculo], en el cual BD y GE son las diagonales, el producto de las diagonales será igual a la suma de los productos de los lados opuestos [por ej. BD * GE = BG * DE + BE * GD]. Por consiguiente, dado que (BD * GE) y (BG * DE) son ambos dados, (BE * GD) es también dado. Pero BE también es dado, siendo [igual a un] diámetro: por lo tanto la parte restante [13], GD, también será dada, y por lo tanto GA, la [cuerda] del suplementario.
Por lo tanto, si dos arcos y las correspondientes cuerdas son dadas, la cuerda correspondiente a la suma de estos arcos será dada por medio de este teorema.
Es obvio que combinando [en este sentido] la cuerda de 1 ½º con todas las cuerdas que ya hemos obtenido, y entonces calcular las cuerdas sucesivas, podremos entrar [en la tabla] todas las cuerdas [de los arcos] que cuando se duplican son divisibles por tres [por ej. múltiplos de 1 ½º]. Luego las únicas cuerdas restantes a ser determinadas serán aquellas [que están] entre los intervalos de 1 ½º, dos en cada intervalo, dado que nuestra tabla esta confeccionada a intervalos de ½º. Por consiguiente, si encontramos la cuerda de ½º grado, esta nos permitirá completar [la tabla con] todas las cuerdas intermedias restantes, encontrando la suma o la diferencia [de ½º] desde las cuerdas dadas a ambos finales de los intervalos [de ½º]. Ahora, si una cuerda, por ej. la cuerda de 1 ½º, esta dada, la cuerda correspondiente a un arco el cual es una tercera [parte] de la previa, uno no la puede hallar por métodos geométricos [14]. (Si esto fuera posible, inmediatamente deberíamos tener la cuerda de ½º). Por consiguiente primeramente derivaremos la cuerda de 1º desde aquellas de 1 ½° y ¾°. Haremos esto estableciendo el lema que, aunque este en general no pueda determinar exactamente los tamaños [de las longitudes de las cuerdas], en el caso de tales cantidades muy pequeñas puedan determinarse con un insignificante pequeño error.
Digo, entonces, que si dos cuerdas distintas son dadas, la proporción de la [cuerda] mayor dividido la [cuerda] menor es menor que la proporción del arco en la [cuerda] mayor dividido el arco en la [cuerda] menor.
[Ver Fig. 1.6.] Sea aquí el círculo ABGD, en el cual son dibujadas dos cuerdas distintas, la más pequeña AB y la más grande BG.

Digo que
GB / BA < arco BG / arco BA.
[Demostración:] Sea el ^ ABG bisecado [dividido en dos] por la [cuerda] BD. Unir AEG, AD y GD. Entonces, dado que el ^ ABG es bisecado por la cuerda BED,
GD = AD
y GE > EA [15].
Entonces eliminar la perpendicular DZ desde D sobre AEG.
Luego, dado que AD > ED y ED > DZ, un círculo dibujado con centro en D con radio DE, cortará AD y pasará más allá de DZ [(hasta Θ)]. Sea aquí dibujado HE, y sea DZ prolongada [hasta] Θ. Ahora, dado que el sector DEΘ es mayor que el triángulo DEZ, y el triángulo DEA [que] es mayor que el sector DEH,
el ∆ DEZ / ∆ DEA < sector DE / sector DEH.
Pero ∆ DEZ / ∆ DEA = EZ / EA [16]
y el sector DE / sector DEH = ^ ZDE / ^ EDA.
por consiguiente ZE / EA < ^ ZDE / ^ EDA.
Entonces, “componendo”,
ZA / EA < ^ ZDA / ^ ADE.
Y, duplicando los primeros miembros [de las proporciones],
GA / EA < ^ GDA / ^ EDA.
Luego, el “dividendo”,
GE / EA < ^ GDE / ^ EDA
pero GE / EA = GB / BA [17]
y ^ GDB / ^ BDA = arco GB / arco BA.
por consiguiente GB / BA < arco GB / arco BA.
Habiendo establecido esto, dibujemos [Fig. 1.7.] un círculo ABG, y en él dos cuerdas, AB y AG. Supongamos, primero, que AB es la cuerda de ¾º y AG la cuerda de 1º. Luego, dado que
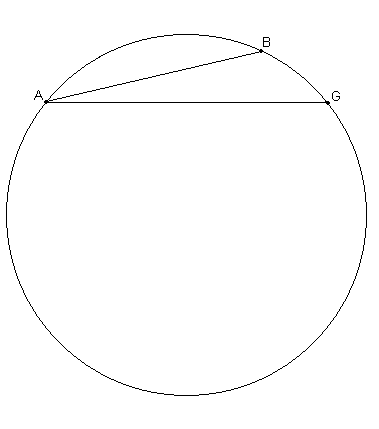
AG / BA < arco AG / arco AB
y arco AG = (4 * arco AB) / 3
GA < (4 * AB) / 3.
Pero, en unidades en las que el diámetro contiene 120p, demostramos que
AB = 0;47,8p
por consiguiente GA < 1;2,50p (para 1;2,50 ≈ (4/3) * 0;47,8).
Nuevamente, utilizando la misma figura, pongamos AB como una cuerda de 1º y AG como una cuerda de 1 ½º. Por el mismo argumento, ya que
arco AG = (3 * arco AB) / 2
GA < (3 * BA) / 2.
Pero en unidades en las que el diámetro contiene 120p, demostramos que
AG = 1;34,15p
por consiguiente AB > 1;2,50p (para 1;34,15 = (3/2) * 1;2,50).
Por lo tanto, dado que la cuerda de 1º fue demostrada ser tanto mayor y menor que la misma cantidad, podemos establecerla como de aproximadamente 1;2,50p donde el diámetro es de 120p. Por las proposiciones precedentes podemos también establecer la cuerda de ½º, que hallamos ser de aproximadamente 0;31,25p. Los intervalos restantes [ahora] se pueden completar, como hemos dicho [Fig. 1.6]. Por ejemplo, en el primer [1 ½º] intervalo podemos calcular la cuerda de 2º utilizando la fórmula de adición para la cuerda de ½º aplicada a la cuerda de 1 ½º, mientras la cuerda de 2 ½º esta dada utilizando la fórmula de la diferencia para [la cuerda de ½º] aplicada a la cuerda de 3º. Similarmente para las cuerdas restantes.
Tal es, pienso, luego, [que] este es el camino más fácil para comprometerse en el cálculo de las cuerdas. Aunque, como he dicho, en orden que podamos tener las presentes cantidades de las cuerdas dispuestas fácilmente para cada ocasión, a continuación expondremos unas tablas [para este propósito].
Ellas están confeccionadas en tablas de 45 líneas [18] [cada una] para dar una apariencia simétrica. La primera columna [en cada sección] contendrá los arcos tabulados a intervalos de ½º, la segunda columna corresponde a las cuerdas en unidades en las que el diámetro contiene 120p, y la tercera columna la trigésima parte del incremento en la cuerda para cada intervalo. Esta última es para que podamos tener el incremento promedio correspondiente a un minuto [de arco], que no será sensiblemente diferente del incremento verdadero [para cada minuto]. Por lo tanto podemos calcular fácilmente la cantidad de las cuerda correspondiente a las fracciones que se ubican entre los intervalos [tabulados] de medio grado.
Es fácil ver esto, si suponemos alguna corrupción [error] del escriba en uno de los valores de las cuerdas de la tabla, los mismos teoremas que ya hemos establecido nos permitirán verificarlos y corregirlos fácilmente, tomando tanto la cuerda de doble arco [de tal] cuerda en cuestión, o desde la diferencia con alguna otra cuerda dada, o desde la cuerda del suplemento.
El diseño de las tablas es el siguiente.
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Libro I |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 | 11 | 12 |
| 13 | 14 | 15 |
| 16 |
Notas de referencia
- ↑ Sobre los cálculos de Ptolomeo en su tabla de cuerdas, ver HAMA 21-4, Pedersen, 56-63.
- ↑ La conveniencia principal es que el radio sea de 60 partes, o 1,0 en el sistema sexagesimal. Por lo tanto, en algunos casos, estos [valores] se parecen a la tabla del Seno con R = 1.
- ↑ Euclides II 6.
- ↑ Euclides VI define 3 estados en la que “una línea recta ha sido cortada en proporción extrema y media cuando, como la línea total es al segmento más grande, entonces es mayor a menor”; por ej. aquí ZG / DG = DG / ZD.
- ↑ Euclides XIII 9.
- ↑ Euclides IV 15.
- ↑ Euclides XIII 10.
- ↑ La lectura 14 (en vez de 15) ocurre como una variante marginal, en el manuscrito griego, aquí y en lugares relacionados (ver apartado en H34,16; 34,18; 36,4 y 36,7 -no presente en esta traducción al español-), y en el Arábigo, en el manuscrito T, y [también] fue adoptado en la traducción de al-Hajjaj. Este es más preciso, pero no hace una diferencia en el resultado final.
- ↑ Leer (en el manuscrito D) en cambio de en H35,18.
- ↑ Esta proposición, comúnmente conocida como el “Teorema de Ptolomeo”, no es de hecho declarado antes que él. Resulta incierto si alguna de las primeras tablas de las cuerdas (por ej. la de Menelao) utilizaron alguna base geométrica más allá del “Teorema del ángulo medio” (Ver nota de referencia siguiente y Toomer [2] 18-19).
- ↑ También la fórmula de Ptolomeo para la cuerda del “ángulo mitad” fácilmente puede ser derivada desde su teorema general (ver Toomer [2] 16-17), él introduce en cambio otro teorema, que se remonta a Arquímedes (ver HAMA 23-4). Es una inferencia válida de que fuera así ya que el último teorema fue la única base de las primeras tablas de cuerdas, notablemente la de Hiparco, como he argumentado, en Toomer [2] 18-19.
- ↑ Euclides VI 8.
- ↑ Leer (en el manuscrito A) en H42,1, en cambio de (“por sustracción”).
- ↑ Esto es válido: el problema de hallar la cuerda α desde la cuerda 3α dada puede ser reducida a una ecuación del tipo cúbica, la cuál no puede ser resuelta (excepto para unos pocos valores de α) por la geometría de Euclides (utilizando la línea recta y el círculo). Ver Toomer [3] 138.
- ↑ Derivado de Euclides VI 3, que establece que la bisectriz del ángulo sobre el ápex (ápice, vértice) de un triángulo divide la base en proporción a dos lados incluyendo el ángulo. Entonces, BG > BA, GE > EA.
- ↑ Euclides VI 1.
- ↑ Euclides VI 3.
- ↑ 45 líneas es la altura estándar de las tablas a través de todo el Almagesto. Probablemente es elegido para conformar algunas alturas estándares de los rollos de papiro (sobre los papiros estándares ver Lewis, “Papyrus in Classical Antiquity”, 36-9, 56, en Plinio NH 13, 78). Varias consecuencias surgen de esto, notablemente el intervalo de 18 años en las tablas de movimiento medio (ver Libro III Capítulo 2 nota de referencia nro. 28).
