Almagesto: Libro V - Capítulo 13
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
{Demostración de las Distancias de la Luna}
En el vigésimo año de Adriano, el 13 de Athyr [III] en el calendario Egipcio [1 de Octubre de 135], 5 ⅚ horas equinocciales después del mediodía, justo antes de la puesta del Sol, observamos la Luna cuando estaba en el Meridiano (Culminación superior). La distancia aparente desde su centro hasta el Cenit, de acuerdo con el instrumento, fue de 50 11/12º. La distancia [medida] sobre el listón delgado fue de 51 7/12 de las 60 subdivisiones dentro de las cuales el radio de una revolución ha sido dividido, y una cuerda de aquel tamaño subtiende un arco de 50 11/12º. Ahora el período de la época desde el primer año de [la era de] Nabonassar hasta el momento de la observación de arriba es de
882 años Egipcios 72 días 5 ⅚ horas equinocciales recontados simplemente
882 años Egipcios 72 días 5 ⅓ horas equinocciales recontados en forma precisa.
Para ese instante hallamos [2]:
la longitud media del Sol: ♎︎ 7;31º
la longitud verdadera del Sol: ♎︎ 5;28º
la longitud media de la Luna: ♐︎ 25;44º
la elongación: 78;13º
la distancia [en anomalía] desde el apogeo medio del Epiciclo: 262;20º
la distancia [del argumento de la] latitud desde el límite Norte: 354;40º.
Por lo tanto la Ecuación Completa de la Anomalía, derivada de la tabla apropiada, fue de +7;26º, entonces la Posición Verdadera de la Luna en ese momento:
en longitud:♑︎ 3;10º
en [el argumento de la] latitud sobre el círculo inclinado: 2;6º desde el límite Norte
en latitud sobre el gran círculo a través de los polos de la Eclíptica (que en ese momento casi coincide con el meridiano): [3] 4;59º al Norte de la eclíptica.
Ahora los ♑︎ 3;10º están a 23;49º al Sur del Ecuador sobre el mismo círculo meridiano, y el Ecuador está, igualmente, a 30;58º al Sur del Cenit en Alejandría. Por lo tanto la distancia verdadera desde el centro de la Luna hasta el Cenit fue de [23;49º + 30;58º - 4;59º =] 49;48º. Y su distancia aparente fue de 50;55º. Por lo tanto la Paralaje de la Luna a la distancia [de la Luna desde la Tierra] correspondiente a la posición en cuestión fue de 1;7º a lo largo del gran círculo a través de la Luna y de los polos del horizonte, cuando su distancia verdadera desde el cenit fue de 49;48º.
Ahora que hemos establecido esto, dibujar [Fig. 5.10] en el plano del gran círculo a través de los polos del horizonte y de la Luna los siguientes grandes círculos, sobre el mismo centro:
AB, aquél el de la Tierra;
GD, aquél a través del centro de la Luna [según] la observación [de arriba];
EZHΘ, el gran círculo en el que la Tierra mantiene la relación de un punto,
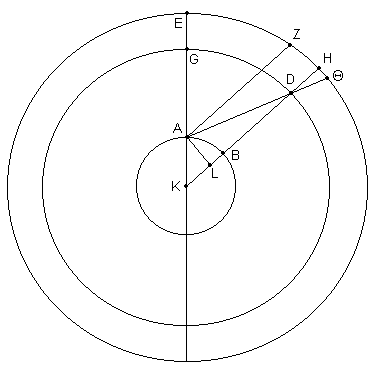
Sea K sus centros en común, y sea KAGE la línea a través de los puntos en el cenit. Asumamos que la misma distancia de la Luna, D, [medida] desde el cenit [ubicado] en G, es la cantidad ya determinada de 49;48º. Unir KDH, ADΘ, y además desde el punto A, que representa el ojo del observador, dibujar AL perpendicular a KB, y AZ paralela a KH.
Entonces, es obvio que para un observador en el punto A la paralaje de la Luna fue [expresada por] el arco HΘ. Entonces el arco HΘ es de 1;7º, de acuerdo a los cálculos desde la observación. Pero dado que el arco ZΘ es insignificantemente mayor que el arco HΘ (toda la Tierra mantiene la proporción de un punto al círculo EZHΘ), el arco ZHΘ es casi el mismo, de 1;7º. Y ya que, nuevamente, el punto A es insignificantemente diferente desde el centro del círculo ZΘ,
^ ZAΘ = 1;7º donde 4 ángulos rectos = 360º
^ ZAΘ = 2;14ºº donde 2 ángulos rectos = 360ºº.
Y ^ ADL = ^ ZAΘ = 2;14ºº.
Por lo tanto en el círculo alrededor del triángulo rectángulo ADL,
arco AL = 2;14º
y Cuerda arco AL = 2;21p donde la hipotenusa AD = 120p.
Pero LD es insignificantemente más pequeña que AD.
Por lo tanto donde LA = 2;21p, LD ≈ 120p.
Además dado que, por hipótesis, el arco GD = 49;48º,
el ángulo en el centro del círculo,
^ GKD = 49;48º donde 4 ángulos rectos = 360º
^ GKD = 99;36ºº donde 2 ángulos rectos = 360ºº.
Por lo tanto en el círculo alrededor del triángulo rectángulo ALK
arco AL = 99;36º
y arco LK = 80;24º (suplementario).
Por lo tanto las cuerdas correspondientes
AL = 91;39p donde la hipotenusa AK = 120p.
y LK = 77;27p donde la hipotenusa AK = 120p.
Por lo tanto donde AK, el radio de la Tierra, es de 1p,
AL = 0;46p
y KL = 0;39p.
Pero donde AL = 2;21p, LD, fue demostrado [ser], = 120p.
Por lo tanto donde AL = 0;46p, LD = 39;6p.
Y, en las mismas unidades, KL = 0;39p.
y el radio de la Tierra, KA = 1p.
Por lo tanto donde KA, el radio de la Tierra, es de 1p,
por adición, KLD, que representa la distancia de la Luna en la observación, es de 39;45p [4].
Ahora que hemos demostrado esto, sea ABG [Fig. 5.11] la Excéntrica de la Luna con centro en D y diámetro ADG, sobre el cuál [el punto] E es tomado como centro de la eclíptica, y Z como punto hacia el cual [el diámetro del apogeo medio del] epiciclo es dirigido. Dibujar el epiciclo, HΘKL, sobre el punto B, y unir HBΘE, BD y BKZ. Sea L representando la posición de la Luna en la observación en cuestión, y dibujar perpendiculares a BE, DM desde D [5] y ZN desde Z.
Entonces, dado que la cantidad de la elongación en el momento de la observación fue de 78;13º [(ver al principio de este capítulo)], continúa desde la teoría previamente establecida que
^ AEB = 156;26º donde 4 ángulos rectos = 360º;
Por lo tanto su suplemento,
^ ZEN = ^ DEM = 23;34º donde 4 ángulos rectos = 360º
^ ZEN = ^ DEM = 47;8ºº donde 2 ángulos rectos = 360ºº.
Por lo tanto en los círculos alrededor de los triángulos rectángulos correspondientes, [ZEN y DEM], [y] dado que DE = EZ,
arco DM = arco ZN = 47;8º
y arco EM = arco EN = 132;52º [suplementario].
Por lo tanto las cuerdas correspondientes
DM = ZN = 47;59p donde la hipotenusa DE = hipotenusa EZ = 120p.
y EM = EN = 110;0p donde la hipotenusa DE = hipotenusa EZ = 120p.
Por lo tanto donde DE = EZ = 10;19p y DB, el radio de la excéntrica, es de 49;41p,
DM = ZN = 4;8p
y EM = EN = 9;27p.
Y dado que BM² = BD² - DM²,
BM = 49;31p.
Y BE = [BM - EM = ] 40;4p,
y, por sustracción [de EN desde BE], BN = 30;37p donde ZN = 4;8p.
Y dado que BN² + ZN² = BZ²,
la hipotenusa BZ = 30;54p.
Por lo tanto en el círculo alrededor del triángulo rectángulo BZN,
donde la hipotenusa BZ = 120p,
ZN = 16;2p
y arco ZN = 15;21º.
En consecuencia ^ ZBN = 15;21ºº donde 2 ángulos rectos = 360ºº
en consecuencia ^ ZBN = cerca de 7;40º donde 4 ángulos rectos = 360º.
Estos [7;40º], entonces, es el tamaño del arco ΘK del epiciclo.
Seguido, la distancia de la Luna desde el apogeo medio del epiciclo en el momento de la observación fue de 262;20º [(ver al principio de este capítulo)], y, obviamente, su distancia desde K, el apogeo medio, fue de 82;20º (por sustracción de un semicírculo).
Por lo tanto arco KL = 82;20º
y arco ΘKL = [arco ΘK + arco KL = ] 90;0º.
Entonces ^ ΘBL es un ángulo recto.
En consecuencia EL² = BL² + EB²,
y donde DB, el radio de la excéntrica, es de 49;41p
y BL, el radio del epiciclo, es 5;15p,
EB, cómo demostramos = 40;4p.
En consecuencia EL = 40;25p.
Por lo tanto la distancia de la Luna en [el momento de] la observación es de 40;25p,
donde BL, el radio del epiciclo, es de 5;15p
y donde EA, la distancia desde el centro de la Tierra al apogeo de la excéntrica, es de 60p,
y donde EG, la distancia desde el centro de la Tierra al perigeo de la excéntrica, es de 39;22p.
Pero demostramos que la distancia de la Luna en la observación, es [decir] EL, fue de 39;45p donde el radio de la Tierra es [igual a] uno [1 parte].
Por lo tanto EL, la distancia de la Luna en la observación, es de 39;45p, y el radio de la Tierra es 1p,
EA, la distancia media en las Sizigias = 59;0p, [6]
EG, la distancia media en los cuadrantes = 38;43p,
y el radio del epiciclo = 5;10p.
Lo que se ha requerido para examinar.
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Libro V |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 | 11 | 12 |
| 13 | 14 | 15 |
| 16 | 17 | 18 |
| 19 |
Notas de referencia
- ↑ Ver HAMA 101-3, Pedersen 204-7.
- ↑ Datos calculados con un programa de computación desde las observaciones realizadas por Ptolomeo (actual Alejandría) de las siguientes:
Posiciones del Sol y de la Luna (Coordenadas Eclípticas, Latitud Sol: 0°) Fecha Hora Longitud Sol Longitud Luna Latitud Luna Elongación Luna Carta 1 de Octubre de 135 d. C. (135) 17:46:22 hs. ♍︎ 186° 49’ 25” ♑︎ 274° 54’ 19” 5° 17’ 55” E 88° 05’ 44” 
Almagesto Observación 01.10.135 d. C Hora de la puesta del Sol: 17:48:05 hs.
Hora de paso de la Luna (meridiano de Alejandría): 17:46:22 hs. (Edad lunar: 7 días 21 horas = Cuarto Creciente).
Altura de la Luna (en paso o Culminación Superior): 40° 29' 18,82".
Distancia Cenital de la Luna: (90° - 40° 29' 18.82") = 49° 30' 41,18".Nota del traductor al español: carta y datos elaborados con mi software de aplicación "M1 Sistema Astronómico"©.
- ↑ Dado que la Luna estuvo casi en el solsticio de invierno (cf. ver al principio de este capítulo).
- ↑ Aquí hay un error acumulado, debido a una serie de pequeñas imprecisiones y redondeos. Un [valor] más preciso podría ser 39;50p.
- ↑ Heiberg correctamente eliminó ("extendido") en H413,7 como un término necesario que "molesta" en la estructura de la sentencia. Transfiriéndolo después como BE (como lo hicieron Halma y Manitius) no siendo una improvisación, dado que la perpendicular desde Z no esta sobre la extensión de BE.
- ↑ Este resultado para la distancia media de la Luna esta bien de acuerdo con los hechos (siendo ligeramente mayor que 60 radios terrestres), y da a entender que la paralaje de Ptolomeo en las sizigias (por ej. en los eclipses solares) es bastante exacta. No obstante, el proceso por el cual esta es determinada contiene un número de errores (en la paralaje observada, en la latitud, en la declinación etc., y en la distancia resultante del modelo de Ptolomeo), que "milagrosamente" se cancelan mutuamente. Por detalles ver HAMA 102-3. Esto no es un accidente: Ptolomeo sabía (aproximadamente) que paralaje tenía que darse en los eclipses, y elegir una observación que produzca tal cantidad. Como sugerencia ver Toomer [9] 131 donde la cifra de 59 radios terrestres ya había sido derivada por Hiparco.
