Almagesto: Libro V - Capítulo 10
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
{Que la diferencia en las Sizigias debida a la Excéntrica de la Luna es insignificante}
Ahora bien, es probable que algunas personas puedan sospechar que el círculo excéntrico de la Luna podría también tener un efecto considerable en las conjunciones y en las oposiciones (Sizigias) y en los eclipses ocurriendo en ellas, dado que el centro del Epiciclo no siempre está, bajo todas las circunstancias, ubicado exactamente en el apogeo en esos instantes, sino que puede estar desplazado desde el apogeo por un arco [de la excéntrica] de tamaño considerable, ya que su ubicación precisamente en el apogeo ocurre en las sizigias medias, mientras la determinación de la conjunción y de la oposición verdaderas requieren tener en cuenta las anomalías de ambas luminarias. Por lo tanto trataremos de demostrar que esta diferencia no puede producir cualquier error considerable en [el cálculo de] los fenómenos en las sizigias, incluso si la corrección debida a la excentricidad no es tomada en cuenta.
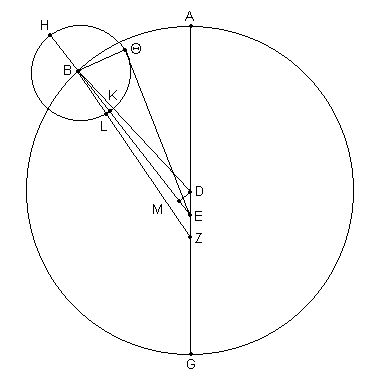
Sea ABG [Fig. 5.8] [2] el círculo excéntrico de la Luna con centro en D y diámetro ADG, sobre el cual el punto E es tomado como centro de la eclíptica, y Z como el punto de la "dirección" [3], opuesto a D. Cortar el arco AB desde el apogeo A, y dibujar el epiciclo HΘKL, con centro en B. Unir BD, HBKE y BLZ.
Ahora la cantidad de la [ecuación] de la anomalía puede diferir de dos maneras desde aquella ubicación del apogeo del epiciclo ([ubicado] en A):
[1] dado que el epiciclo esta desplazado hacia el perigeo, el epiciclo subtiende un ángulo mayor en E;
[2] la dirección en la cual apunta el diámetro a través del apogeo medio y del perigeo [del epiciclo] no es mayor hacia E sino hacia Z.
El efecto desde el primer factor es un máximo cuando la Ecuación de la Anomalía de la Luna es máxima, mientras que el efecto del segundo factor es un máximo cuando la Luna esta cerca del apogeo o del perigeo del epiciclo. Por ende esta claro que cuando ocurre el efecto máximo del primer factor, el efecto del segundo factor será muy insignificante, dado que la ecuación de la anomalía de la Luna apenas varía en una distancia considerable a ambos lados de su ubicación sobre la tangente del epiciclo. Sin embargo, [en esta ubicación] la sizigia verdadera puede diferir de la media por la suma de las ecuaciones de las dos luminarias, si una es aditiva y la otra sustractiva. Por otro lado, cuando ocurre el efecto máximo del segundo factor, [es decir] la diferencia debida a la dirección, entonces nuevamente el efecto del primer factor es insignificante, dado que la ecuación completa de la anomalía es tanto [igual a] cero o muy pequeña cuando la Luna esta cerca del apogeo o del perigeo del epiciclo. Pero [en este caso] la sizigia verdadera diferirá de la media solo por la ecuación de la anomalía del Sol.
Supongamos, entonces, que el Sol tiene una máxima ecuación aditiva de 2;23º, y que también (primero) la Luna tiene una máxima ecuación (pero sustractiva) de 5;1º. Por consiguiente el ^ AEB tiene el doble de la suma del [valor] de arriba de 7;24º, por ej. 14;48º. Dibujar EΘ desde E tangente al epiciclo, y eliminar la perpendicular BΘ hasta ella, y también la perpendicular DM desde D hasta BE. Entonces dado que
^ AEB = 14;48º donde 4 ángulos rectos = 360º
^ AEB = 29;36ºº donde 2 ángulos rectos = 360ºº,
en el círculo alrededor del triángulo rectángulo DEM
arco DM = 29;36º
y arco EM = 150;24º (suplementario).
Por lo tanto las cuerdas correspondientes
DM = 30;39p donde la hipotenusa DE = 120p.
y EM = 116;1p donde la hipotenusa DE = 120p.
Por lo tanto DE, la distancia entre los centros, es de 10;19p, y BD, el radio de la excéntrica, es de 49;41p,
DM = 2;38p
y EM = 9;59p.
Y dado que BM² = BD² - DM²,
BM = 49;37p,
y, por adición [de EM], BME = 59;36p, donde BΘ, el radio del epiciclo, es de 5;15p.
Por consiguiente, en el círculo alrededor del triángulo rectángulo BEΘ,
donde la hipotenusa EB = 120p,
BΘ = 10;34p,
y arco BΘ = 10;6º.
Por lo tanto, el ángulo de la máxima ecuación de la anomalía,
^ BEΘ = 10;6ºº donde 2 ángulos rectos = 360ºº
^ BEΘ = 5;3º donde 4 ángulos rectos = 360º,
en cambio de los 5;1º de la posición del apogeo del epiciclo en A.
Por lo tanto la diferencia en la ecuación de la anomalía debida a este efecto, fue hallada ser de 2 sexagésimas partes de un grado, que incluso no puede producir un error tanto como la 1/16 ta. parte de una hora [4].
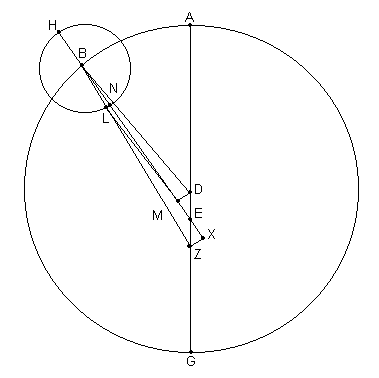
Seguido, sea la Luna [ubicada] en L, el perigeo medio. Por lo tanto el ^ AEB contendrá, aproximadamente, solo el doble [del máximo] de la ecuación de la anomalía del Sol, a saber 4;46º. Con una figura [Fig. 5.9] similar [a la precedente], dibujar la línea EL, y eliminar las perpendiculares LN (desde L) y DM (desde D) hasta BE, y ZX desde Z hasta la [línea] prolongada BE. Luego, por el mismo tipo de cálculo como el [descrito] anteriormente, dado que el ángulo en E,
[^ AEB] = 4;46º donde 4 ángulos rectos = 360º
[^ AEB] = 9;32ºº donde 2 ángulos rectos = 360ºº,
en los círculos alrededor de los triángulos rectángulos EDM y EZX,
arco DM = arco ZX = 9;32º
y arco EM = arco EX = 170;28º (suplementarios).
En consecuencia Cuerda arco DM = Cuerda arco ZX = 9;58p, donde las hipotenusas DE y EZ = 120p.
y Cuerda arco ME = Cuerda arco EX = 119;35p, donde las hipotenusas DE y EZ = 120p.
Por lo tanto, donde DE = EZ = 10;19p
y DB, el radio de la excéntrica, es de 49;41p,
DM = ZX = 0;51p
y ME = EX = 10;17p.
Y dado que BM² = BD² - DM²,
BM ≈ 49;41p.
En consecuencia BE = [BM + ME =] 59;58p,
y, por adición [de EX], BX = 70;15p donde ZX = 0;51p.
Por lo tanto, con el mismo argumento, la hipotenusa BZ [del triángulo BZX] será aproximadamente del mismo tamaño [de BX], de 70;15p.
Y BZ / ZX = BL / LN y BZ / BX = BL / BN.
Por consiguiente BL, el radio del epiciclo, es de 5;15p,
y BE, fue demostrado = 59;58p,
LN = 0;4p y BN ≈ 5;15p,
y, por sustracción [de BN desde BE], NE = 54;43p donde LN = 0;4p.
Y dado que, según lo precedente, la hipotenusa EL [del triángulo ELN] no es notablemente diferente de esta cantidad de 54;43p, continua que, donde la hipotenusa EL = 120p,
LN ≈ 0;8p,
y, en el círculo alrededor del triángulo rectángulo ELN,
arco LN = 0;8p.
Por lo tanto la diferencia en la posición de la Luna debida a la dirección hacia Z,
^ BEL = 0;8ºº donde 2 ángulos rectos = 360ºº
^ BEL = 0;4º donde 4 ángulos rectos = 360º [5].
Por lo tanto aquí también la diferencia en la ecuación de la anomalía de la Luna es [de sólo] 4 minutos de arco; e incluso no produce un error significante en el fenómeno en las sizigias, dado que esta no puede alcanzar mucho más que ⅛ va. parte de una hora, cantidad que con frecuencia uno puede esperar encontrar como un error puramente observacional.
Hemos realizado las argumentaciones anteriores, no para demostrar que uno no puede tomar en cuenta esas diferencias, aunque también sean muy pequeñas, para los cálculos de las sizigias, sino para demostrar que no hemos cometido un notable error en nuestras demostraciones iniciales utilizando los eclipses lunares cuando usamos [la hipótesis simple], y no aquella suplementaria introduciendo la excéntrica.
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Libro V |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 | 11 | 12 |
| 13 | 14 | 15 |
| 16 | 17 | 18 |
| 19 |
Notas de referencia
- ↑ Ver HAMA 98-9.
- ↑ La Fig. 5.8 esta dibujada erróneamente en el texto de Heiberg, donde D ha sido unida en cambio de la tangente E. Este es un error de Heiberg, no confirmado en el manuscrito, y corregido por Manitius.
- ↑ . Ver el Libro V Capítulo 5 nota de referencia nro. 2.
- ↑ Por el tiempo [que toma] un eclipse ver el Libro III Capítulo 2 nota de referencia nro. 16.
- ↑ El resultado final de Ptolomeo es correcto (al minuto más cercano), aunque algunos de los resultados intermedios son imprecisos. Por ej., justamente arriba en el cálculo de LN, 0;4 * 120 / 54;43 esta más cerca de 0;9 que de 0;8. Parece como si [Ptolomeo] lo calculó para dos lugares fraccionarios sexagesimales, y entonces deja un poco confusos los resultados en la presentación.
