Almagesto: Libro V - Capítulo 19
| Capítulo Anterior | Contenidos | Ir al Libro VI - Capítulo 1 |
{Sobre la determinación de las Paralajes}
Entonces, cuando decidimos determinar la cantidad de la Paralaje de la Luna en cualquier posición [lunar] dada, (primero) con respecto al gran círculo dibujado a través de la Luna y del Cenit, examinamos su distancia (en horas equinocciales) desde el Meridiano en la latitud en cuestión. Con la distancia encontrada como argumento, entramos en la Tabla de los Ángulos y de los Arcos para la latitud y los signos del Zodíaco apropiados, y tomamos la cantidad en grados en la segunda columna correspondiente a la hora, interpolando entre horas enteras si fuera necesario [2]. Esto nos da la distancia de la Luna desde el Cenit, medido a lo largo del gran círculo uniendo a los dos [(la Luna con el cenit)]. Con esta [distancia] como argumento, entramos en la Tabla de las Paralajes, determinando sobre que línea en la primera columna el argumento es hallado, y tomando los números correspondientes a este [argumento] en las [otras] cuatro columnas, siguiendo la columna de las paralajes solares, a saber, la tercera, la cuarta, la quinta y la sexta columna, escribiendo cada una separadamente. Entonces tomamos en ese momento la anomalía corregida (por ej. con respecto al apogeo verdadero del Epiciclo): [si este es menor que 180º,] tomamos la anomalía misma, pero si esta es mayor que 180º, tomamos (360º menos la anomalía); dividimos siempre la cantidad obtenida, y, entrando con ella dentro de la misma [columna del los] argumentos, determinamos el número de minutos correspondientes a esta [cantidad] separadamente en ambas columnas, la séptima y la octava. Tomamos los minutos encontrados en la séptima columna, multiplicándolos por la diferencia encontrada en la cuarta columna, y (siempre) adicionamos [sumamos] el resultado a la paralaje desde la tercer columna. [Asimismo] tomamos los minutos encontrados desde la octava columna, multiplicándolos por la diferencia encontrada en la sexta columna, y nuevamente adicionamos (siempre) el resultado a la paralaje de la quinta columna. Por lo tanto hemos obtenido dos paralajes; tomamos la diferencia entre esas y la escribimos. Seguido tomamos la Elongación Media de la Luna desde el Sol, sino la elongación media de la Luna desde el punto opuesto de la posición media del Sol, la menor [3] de cualquiera de estas dos distancias, y entrando con esta también dentro de los argumentos en la primera columna, tomamos los minutos correspondientes a ella en la novena y en la última columna. Multiplicamos esos [minutos] por la diferencia entre las dos paralajes que escribimos, y (siempre) adicionamos el resultado a la más pequeña (esta es, la única derivada desde la tercera y desde la cuarta columna). Esta suma nos dará la Paralaje de la Luna medida a lo largo del gran círculo a través de la Luna y del cenit.
La paralaje del Sol, en una situación similar (por ej. medida a lo largo de un círculo de Altitud), inmediatamente es determinada, de una manera sencilla, (para los eclipses solares), desde el número en la segunda columna correspondiente al tamaño del arco desde el cenit [hasta el Sol] [4].
Ahora con el fin de determinar, en un instante dado, la Paralaje con respecto a la Eclíptica, tanto en Longitud como en Latitud, entramos nuevamente, con la misma distancia de la Luna [medida] desde el meridiano en horas equinocciales [como lo hicimos antes], dentro de la misma parte de la Tabla de los Ángulos y de los Arcos, y tomamos el número de grados correspondientes a aquella hora, en la tercera columna si la Luna esta al Este del meridiano, o en la cuarta columna si esta al Oeste del Meridiano. Examinamos el resultado, y si este es menor que 90º escribimos el mismo número; pero si este es mayor que 90º, escribimos su suplemento, dado que será la cantidad en grados del menor de los dos ángulos en la intersección [de la eclíptica y del círculo de altitud] en cuestión.
Duplicamos el número escrito, y entramos con este número [duplicado], y también con su [ángulo] suplementario, dentro de la Tabla de las Cuerdas. La proporción [el tamaño] de la cuerda del número duplicado sobre la cuerda del suplemento dará la proporción de la Paralaje Latitudinal sobre la Paralaje Longitudinal (dado que arcos circulares de tal pequeño tamaño no son notablemente diferentes de las líneas rectas). Entonces multiplicamos las cantidades de las cuerdas en cuestión por la paralaje determinada con respecto al círculo de altitud, y dividimos los productos, cada uno separadamente, por 120. Los resultados de la división nos dan los componentes separados de la paralaje. Aplicamos las siguientes reglas generales.
Para la Paralaje Latitudinal, cuando el cenit esta al Norte del punto de la eclíptica entonces culminando, sobre el meridiano, el [efecto de la] paralaje será [ocurrirá] hacia el Sur de ella [de la eclíptica]; pero cuando el cenit esta al Sur del punto del punto de culminación, [el efecto de] la paralaje en latitud será hacia el Norte.
En cuanto a la Paralaje Longitudinal: los ángulos tabulados en la (Tabla II 13) representan el [ángulo] de más al Norte de los dos ángulos cortados hacia la parte trasera de la intersección de la eclíptica [con el círculo de Altitud] [5]. Por lo tanto, cuando la paralaje latitudinal esta al Norte, si el ángulo en cuestión es mayor que un ángulo recto, el efecto de la paralaje longitudinal será [ocurrirá] hacia adelante [por ej. en orden reverso] de los signos, pero si el ángulo es menor que un ángulo recto, el efecto será hacia la partes traseras [por ej. en el orden de los signos]. No obstante, cuando la paralaje latitudinal esta al Sur, el [efecto] reverso será verdadero: si el ángulo en cuestión es mayor que un ángulo recto, la paralaje longitudinal estará hacia la parte de atrás [por ej. del orden] de los signos, aunque si esta es menor que un ángulo recto, la paralaje longitudinal estará hacia adelante [6].
Nuestras previas demostraciones concernientes al Sol desarrolladas sobre la asunción de que este no tiene una paralaje perceptible, a pesar de que somos conscientes que la paralaje, la cual, como subsecuentemente demostramos, también afecta al Sol, hará alguna diferencia en ellas [7]. Sin embargo, no pensamos que el error resultante en [la predicción] del fenómeno será motivo suficiente de preocupación para cambiar necesariamente cualquiera de los teoremas construidos sin tomar un mínimo efecto en consideración. Similarmente, para las paralajes lunares, consideramos suficiente utilizar los arcos y los ángulos formados por el gran círculo a través de los polos del Horizonte [por ej. un círculo de altitud] sobre la eclíptica, en cambio de aquellos en el círculo inclinado de la Luna. Ya que vimos que es imperceptible la diferencia que podría resultar en las Sizigias en las cuales los eclipses ocurren, y establecimos que lo último podría haber sido complicado de demostrar y laborioso en calcular; ya que la distancia de la Luna desde el Nodo no es fija para una posición dada de la Luna sobre la eclíptica, sino que sufre cambios múltiples, ambos en cantidad y en [su] posición relativa.
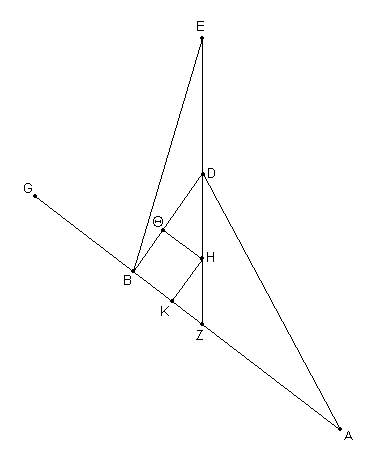
Con el fin de hacer claro lo que queremos decir, sea ABG [Fig. 5.16] un segmento de la eclíptica, AD un segmento del círculo inclinado de la Luna, apuntando al nodo A, y D el centro de la Luna. Dibujar DB en ángulos rectos a la eclíptica. Sea E el polo del horizonte, y dibujar a través de E los arcos EDZ del gran círculo a través del centro de la Luna, y EB a través de B. Sea DH el arco que representa la paralaje de la Luna, y a través del punto H [8] dibujar HΘ a ángulo recto hasta BD y HK a ángulo recto hasta BZ. Por lo tanto AB representa la distancia verdadera [de la Luna] en longitud desde el nodo, y AK la distancia aparente, mientras BD representa la distancia verdadera en latitud desde la eclíptica, y KH la [distancia] aparente. Además un arco igual a ΘH representa el componente longitudinal de la paralaje (con respecto a la eclíptica) derivado desde DH, y un arco igual a DΘ representa el componente latitudinal de la paralaje.
De los teoremas precedentes, [sabemos que] la paralaje DH puede ser hallada si el arco ED es dado, y ambos [componentes de] la paralaje, DΘ y ΘH, si el ^ GZE es dado. Pero lo que determinamos previamente fueron los arcos y ángulos formados en puntos dados de la eclíptica por el círculo de altitud; y B es solamente el punto sobre la eclíptica en la cual esta dado en esta situación. Por lo tanto es claro que estamos utilizando el arco EB en cambio del arco ED, y el ^ GBE en cambio del ^ GZE.
Ahora, Hiparco intenta también corregir este tipo [de imprecisión], aunque es aparente ya que atacó el problema con mucho descuido y de manera irracional [9]. Porque, primeramente, lo hace [justamente] para un único valor de la distancia AD, en cambio de todos los valores [posibles], o por un número de valores, como podría haber sido lo apropiado en una situación donde uno habría elegido ser muy preciso acerca de los pequeños [errores]. Además, sin realizarlo, él ha caído dentro de un número de errores incluso extraños. Habiendo previamente demostrado [como nosotros] también [las cantidades de] los arcos y de los ángulos con respecto a [las intersecciones de los círculos de altitud con] la eclíptica, y demostrado que, si ED esta dado, DH puede ser hallado (lo demuestra en el [Libro I] de su [obra] "Sobre las Paralajes"), con el fin de tomar ED como una cantidad dada, asume que el arco EZ y el ^ EZG son dados (de esa manera, en el [Libro II], calcula ZD y toma ED como remanente [de EZ - ZD]). Sin embargo olvidó por error [propio] notar que el punto dado de la Eclíptica no es Z sino B, y por consiguiente el arco dado no es EZ, sino EB, y el ángulo dado no es EZG sino EBG. Sin embargo son esos [los arcos EZ y el ^ EZG] los que [necesariamente] fueron los puntos de partida incluso para hacer una corrección parcial. Dado que en algunas situaciones existe allí una diferencia bastante notable entre el arco ED y el arco EZ [10], donde la diferencia entre BE (que realmente esta dada) y ED es, a lo sumo, la cantidad del arco BD por alguna distancia dada [de la Luna] desde el nodo.
El procedimiento lógico para realizar la corrección mediante un método [matemáticamente] sólido se puede demostrar de la siguiente manera.
[Primero, ver Fig. 5.17], sea ABG sea la eclíptica, y DBE en ángulos rectos hacia ella. Sea la Luna tanto en D o en E, a una distancia latitudinal desde la eclíptica ABG, la cual es un arco dado, por ej. BD o BE. Entonces los arcos cenitales y los ángulos están dados en el punto B de la eclíptica, y los [arcos y ángulos correspondientes] en [los puntos de la eclíptica] D o E a ser hallados.

Ahora, si la posición de la eclíptica es tal que esta a ángulos rectos hasta el gran círculo dibujado a través del punto Z (que establecimos como polo del horizonte) y apunta hacia B, por ej. ZB, es obvio que este gran círculo coincidirá con el arco DE, y los ángulos en D y E no diferirán de aquel dado en B: dado que [los arcos] dibujados a través de esos puntos [desde el Cenit] están también a ángulos rectos con respecto a la eclíptica.
Y ZD = ZB - BD
ZE = ZB + BE, donde ambos BD y BE son dados.
[Segundo], sea ABG la eclíptica [que] coincide con el gran círculo a través del cenit. Luego [ver Fig. 5.18] si tomamos A como el polo del horizonte y dibujamos AD y AE, estos [dos arcos] diferirán del arco AB, y los ángulos BAD y BAE diferirán desde [el ángulo correspondiente] en el caso previo, cuyo [valor] fue cero [11].

Y AD y AE son dados desde las cantidades AB y BD, BE (hablamos en términos de líneas rectas, dado que es insignificante la diferencia [desde los arcos]),
desde AB² + BD² = AD²
AB² + BE² = AE².
Y los ángulos BAD y BAE pueden por lo tanto ser derivados.
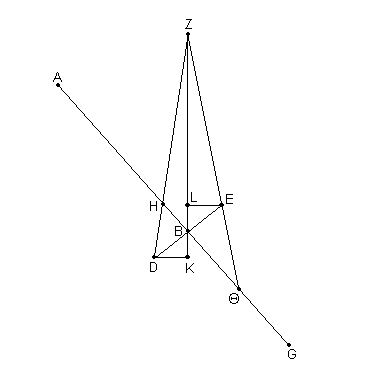
[Tercero,] sea la eclíptica inclinada [al círculo de altitud]. Si [Fig. 5.19] tomamos Z como el polo del Horizonte y dibujamos ZB, ZHD y ZEΘ, el arco ZB y ^ ABZ será dado, y entonces nuevamente, obviamente, lo serán BD y BE. Lo que necesitamos que sean dados son los arcos ZD y ZE, y los ángulos AHZ, AΘZ. Esos también son dados si las perpendiculares DK y EL son dibujadas hasta ZB.
Dado que el ^ ABZ es dado, y el ^ ABE es siempre un ángulo recto, los triángulos rectángulos BKD y BLE son dados, y entonces la proporción es de ZB con los lados conteniendo el ángulo recto, ya que es dada [la proporción de ZB] con las hipotenusas DB y BE. Por lo tanto será dada ZD, la hipotenusa [del triángulo rectángulo ZDK, del cual son dados los lados ZK y KD], y ZE, la hipotenusa [del triángulo rectángulo ZLE, del que son dados los lados ZL y LE], y también los ángulos DZK y EZL, que son las diferencias desde los ángulos requeridos. Dado que
^ AHZ = ^ ABZ + ^ DZB
y ^ AΘZ = ^ ABZ - ^ EZL.
Esta claro que, para la misma distancia latitudinal, la máxima diferencia [con respecto a los arcos y a los ángulos en B] ocurrirá
[1] para los ángulos, cuando el mismo punto B es el cenit. Ya que si el ángulo [formado por el círculo de altitud a través de la Luna] en B es [igual a] cero, los [arcos] a través de D y E desde el cenit forman ángulos rectos con la eclíptica;
[2] para los arcos
- [a] en la misma ubicación [por ej. cuando el punto B esta en el cenit]. Porque cuando el arco [desde el cenit] hasta B es [igual a] cero, los arcos hasta D y E serán iguales en tamaño a la latitud de la Luna; también
- [b]cuando el círculo a través del cenit es perpendicular a la eclíptica. Porque la diferencia entre el arco ZB y ZD o ZE será nuevamente igual a la cantidad total de la latitud [lunar].
- [a] en la misma ubicación [por ej. cuando el punto B esta en el cenit]. Porque cuando el arco [desde el cenit] hasta B es [igual a] cero, los arcos hasta D y E serán iguales en tamaño a la latitud de la Luna; también
Pero en otra situaciones, en las que DE esta inclinada a ZB, las diferencias resultantes entre los arcos y los ángulos serán menores. Por lo tanto, cuando la distancia de la Luna en latitud desde la eclíptica es [igual a] 5º, la máxima diferencia en las paralajes [como calculadas en la eclíptica y en la órbita de la Luna] será alrededor de 10 minutos. Dado que los 5º, representando la mayor diferencia entre los arcos, producen [generan] este número de minutos (cuando uno entra en la Tabla del Libro V Capítulo 18) en la mínima distancia y en la máxima diferencia. Pero cuando la Luna esta en la máxima latitud que puede alcanzar en un eclipse solar, que es alrededor de 1 ½º, la diferencia entre las paralajes será el mismo número, [por ej.] 1 ½, de minutos. Y esto sucede raramente [12].
Un método conveniente para hacer la anterior clase de corrección de los ángulos y los arcos, si alguno quiere hacerlo cuando las [diferencias] involucradas son tan pequeñas, podría ser el siguiente.
Como regla general, duplicamos la cantidad del ángulo [entre el círculo de altitud y la eclíptica], y entrando con ello como un argumento dentro de la Tabla de las Cuerdas tomar la cuerda correspondiente a esta [cantidad], y también la cuerda correspondiente a su suplemento. Multiplicamos ambas por separado por la latitud [de la Luna], en grados, dividimos cada uno de los productos por 120, y registramos los resultados [separadamente]. Como el resultado derivado desde el primer ángulo, lo sustraemos desde el arco relevante desde el cenit [hasta la eclíptica] cuando la Luna esta sobre el mismo lado [de la eclíptica] como el cenit, pero lo adicionamos cuando esta sobre el lado opuesto [de la eclíptica hasta el cenit]. Elevamos al cuadrado el resultado, adicionamos esto [último] al resultado derivado desde el ángulo suplementario, también [elevado] al cuadrado, y tomamos la raíz cuadrada de la suma: esta nos dará el arco correspondiente [ZE o ZD en la Fig. 5.19] que es el requerido.
Seguidamente tomamos el resultado que registramos desde el [segundo,] ángulo suplementario, multiplicándolo por 120, y dividiendo el resultado por el arco encontramos [ZE o ZD]. Con la [cuerda] resultante entramos dentro del [cuerpo de la] Tabla de las Cuerdas, tomamos el arco correspondiente [en la columna del argumento], y lo dividimos. Si el arco corregido [ZE o ZD] es mayor que el original [ZB] adicionamos el resultado a la cantidad del ángulo original, pero si [el arco corregido es] menor [que el original], lo sustraemos: el resultado será el ángulo corregido.

Para dar un ejemplo, en la figura previa [5.20] sea el arco ZB de 45º, ^ ABZ de 30º, y arcos el DB y el arco BE ambos de 5º en latitud.
Ahora la Cuerda (2 * 30)º = Cuerda 60º = 60p,
y Cuerda (180 - 60)º = Cuerda 120º ≈ 104p,
en consecuencia BL / LE = BK / DK [13] = 60 / 104, donde la hipotenusa [BE o BD] = 120p.
Entonces multiplicamos cada numero por 5º de la hipotenusa y los dividimos por 120.
En consecuencia KB = BL = 2;30º
y DK = EL = 4;20º.
Primero supongamos [que] la Luna esta en E:
entonces sustraemos los 2;30º desde los 45º del arco ZB, dado que la distancia a la Luna en latitud esta en la misma dirección como [lo está] el cenit (por ej. ellas están ambas al Sur o al Norte de la eclíptica).
Por lo tanto arco ZL = 42;30º.
Segundo, suponer que la Luna esta en el punto D. Entonces sumamos [2;30º] a los 45º, ya que las posiciones relativas se invierten, y
ZK = 47;30º.
Formamos tanto ZL² + EL² = 42;30² + 4;20²
o ZK² + DK² = 47;30² + 4;20²,
y tomamos tanto ZE ≈ 42;46º
o ZD ≈ 47;44º.
Multiplicamos 4;20 por 120 y lo dividimos por 42;46 y por 47;44 separadamente.
Entonces EL ≈ 12;8p donde la hipotenusa ZE = 120p
y DK ≈ 10 ⅚p donde la hipotenusa ZD = 120p.
El arco correspondiente a la cuerda 12;8p es alrededor de 11 ⅗º
y el arco correspondiente a la cuerda 10 ⅚p es alrededor de 10 ⅓º.
Tomando la mitad de estos [arcos], sustraemos el ^ EZL, [a saber] 5 4/5º, desde el ^ ABZ, por ej. 30º, dado que el arco ZE es menor que el arco ZB.
Por lo tanto ^ AΘZ = 24 ⅕º;
y sumamos el ^ DZK, [a saber] 5 ⅙º, al mismo [^ ABZ, por ej.] de 30º,
dado que el arco ZD es mayor que el arco ZB.
Por lo tanto ^ AHZ = 35 ⅙º.
Tal es el procedimiento que fue requerido [14].
| Capítulo Anterior | Contenidos | Ir al Libro VI - Capítulo 1 |
| Libro V |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 | 11 | 12 |
| 13 | 14 | 15 |
| 16 | 17 | 18 |
| 19 |
Notas de referencia
- ↑ Ver HAMA 114-17, Pedersen 217-19.
- ↑ Literalmente "tanto en in toto, o en la cantidad proporcional para la fracción de una hora".
- ↑ Por ej. (ver HAMA 114) tomamos como argumento η' (que no puede exceder los 90º), derivados desde la elongación media seg. η de acuerdo con las reglas 0 <= seg. η <= 90 / η' = seg. η; 90 <= seg. η <= 180 / η' = 180 - seg. η; 180 <= seg. η <= 270 / η' = seg. η - 180; 270 <= seg. η <= 360 / η' = 360 - seg. η.
- ↑ Para el calculo de una paralaje ver Cálculos, Ejemplo 10.
- ↑ Cf. Libro II Capítulo 10.
- ↑ Ver la última parte de Cálculos, Ejemplo 10.
- ↑ Por ej., en ninguna parte de los Libros III al V las correcciones fueron hechas sobre la posición solar para tomar en cuenta la paralaje, aunque en algunos casos esta podría teóricamente hacer la diferencia (por ej. en observaciones realizadas con el astrolabio con el que ambos el Sol y la Luna fueron observados, Libro V Capítulo 03).
- ↑ Leer H (en el manuscrito Ar, D) en cambio de ' en H449,16. Sugerido por Heiberg y adoptado por Manitius.
- ↑ Ninguno ha dado una explicación satisfactoria del procedimiento de Hiparco, que aquí Ptolomeo alude. Papo de Alejandría dedica una sección de su comentario a él (Rome [1] I 151-5), pero su reconstrucción del método de Hiparco parece enteramente ficticia (ver HAMA 323-5); hay errores en el texto de Rome y se denota ad loc.
- ↑ En situaciones certeras (cf. Tabla Libro II Capítulo 13) el ángulo entre el círculo de altitud y la eclíptica (^ EZA en Fig. 5.16) puede ser cercano a los 180º: entonces el ángulo entre el círculo de altitud y la órbita de la Luna (^ EDA) también será cercano a los 180º, y por lo tanto DZ será un gran arco, y el error de tomar EZ en cambio de ED puede ser considerable, por cuanto el error de tomar EB en cambio de ED no puede exceder el arco BD que (dado que el ^ DBA es un ángulo recto) no puede exceder los 5º, la inclinación de la órbita de la Luna. Después a esto lo eliminé, en H451,12-13, δία , "porque el [ED] anterior esta aún más lejos del siendo dado que del último [EZ]", como una interpolación que es una explicación (muy lamentable) de lo precedente (de hecho esto es una consecuencia, no una causa). La puntuación de Heiberg de este pasaje lo hace ininteligible: elimina el punto después de EZΓ (línea 9) e inserta una coma antes de (línea 10).
- ↑ Literalmente "que no existe". El ángulo en cuestión es el ^ BZD en Fig. 5.17.
- ↑ Para verificar estas cifras, tomar las entradas a intervalos de 5º en la Tabla Libro V Capítulo 18, utilizando las columnas 5° y 6° (que son elegidas porque dan la máxima diferencia). La tasa de cambio es más rápida cerca de cero, por lo tanto: para el argumento 0;0 + 0 = 0; para el argumento 5º, 0;7,30 + 0;2,5 = 0;9,35 ≈ 10'. Ya que los eclipses que ocurren en las conjunciones, tenemos que tomar los valores de la 3° y 4° columnas. Aquí, entre 0º y 1 ½º, encontramos: 0 + 0 = 0,0;1,25 + 0;0,18 = 0;1,43 (que esta más cerca de 1 ¾' que de 1 ½'). La máxima latitud de la Luna en el eclipse solar es alrededor de 1 ½º, la suma del radio aparente de los cuerpos (cada uno cerca de ¼º) y la máxima paralaje en la conjunción (alrededor de 1º; ver Libro VI final del Capítulo 6). No existe la razón de suponer aquí una interpolación, Manitius (p. 447): ha malentendido el pasaje, notablemente mal traducido , H455, 15-16.
- ↑ Cambiar el 'punto y aparte' por una coma después de seg. en H457,7.
- ↑ También uno podría esperar esto, como Neugebauer (en HAMA 116, el cual da un recuento incorrecto del procedimiento de Ptolomeo) establece que este método, que trata los grandes triángulos esféricos ZBD y ZBE como triángulos planos, derivarían a grandes inexactitudes, [pero] esto no es así (como he verificado tomando los peores casos posibles): la razón es que las bases de estos triángulos son pequeñas (BD y BE no pueden exceder los 5º, siendo la máxima latitud Lunar).
