Almagesto: Libro V - Capítulo 17
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
{Sobre las Paralajes individuales del Sol y de la Luna}
Con lo anterior como base, el siguiente problema es demostrar, de nuevo brevemente, cómo uno puede calcular las paralajes individuales del Sol y de la Luna desde las cantidades de sus distancias. Primero [nos ocuparemos con] las paralajes respecto del gran círculo dibujado a través del Cenit y del cuerpo [2].
[Ver Fig. 5.13.] Entonces, en el plano de este gran círculo, sea AB el gran círculo representando la [superficie de la] Tierra nuevamente (como en la Fig. 5.10), GD el gran círculo representando [la posición del] Sol o de la Luna, y EZHΘ el gran círculo con el que la Tierra mantiene la proporción [tamaño] de un punto.
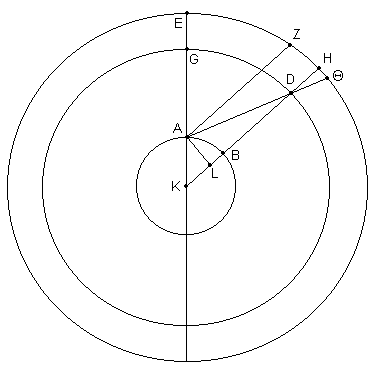
Sea K el centro de todos [esos círculos], y KAGE el diámetro a través del cenit. Cortar el arco GD desde el punto G del cenit; sea éste, por ej. de 30º, y nuevamente dibujar KDH y ADΘ, desde A dibujar AZ [línea] paralela a KH, y eliminar la perpendicular AL hasta KH.
Ahora, ninguna de las luminarias permanecen siempre a la misma distancia. Pero la diferencia resultante en las paralajes del Sol serán muy pequeñas e imperceptibles, dado que la excentricidad de su círculo es pequeña, y su distancia mayor. Sin embargo, ya que para la Luna la diferencia resultante será muy perceptible, tanto porque su movimiento sobre el Epiciclo y el movimiento del epiciclo sobre la Excéntrica, cada uno produce una diferencia bastante grande en la distancia.
Por lo tanto demostraremos las paralajes solares para una única proporción, a saber 1210 / 1, aunque [también] demostraremos las paralajes lunares para las cuatro proporciones que serán las más convenientes para los métodos que desarrollaremos subsecuentemente. Las cuatro distancias que hemos elegido son las siguientes:
Las dos primeras son
[1] cuando el epiciclo esta en el apogeo de la excéntrica,
- [a] la distancia hasta el apogeo del epiciclo, que concluimos desde nuestra demostración previa, ser de 64;10 radios terrestres (ver el Libro V Capítulo 15);
- [b] la distancia hasta el perigeo del epiciclo, que calculamos ser de [59;0 - 5;10 =] 53;50 radios terrestres.
- [a] la distancia hasta el apogeo del epiciclo, que concluimos desde nuestra demostración previa, ser de 64;10 radios terrestres (ver el Libro V Capítulo 15);
Las dos segundas son
[2] cuando el epiciclo esta en el perigeo de la excéntrica,
- [a] la distancia al apogeo del epiciclo, que concluimos desde nuestra demostración previa, ser de [38;43 + 5;10 =] 43;53 radios terrestres (ver al final del Libro V Capítulo 13);
- [b] la distancia al perigeo del epiciclo, que calculamos como de [38;43 - 5;10 =] 33;33 radios terrestres.
- [a] la distancia al apogeo del epiciclo, que concluimos desde nuestra demostración previa, ser de [38;43 + 5;10 =] 43;53 radios terrestres (ver al final del Libro V Capítulo 13);
Entonces, dado que el arco GD = 30º, por hipótesis,
^ GKD = 30º donde 4 ángulos rectos = 360º
^ GKD = 60ºº donde 2 ángulos rectos = 360ºº.
Por lo tanto en el círculo alrededor del triángulo rectángulo AKL
arco AL = 60º,
y arco KL = 120° (suplementario).
Por lo tanto las correspondientes cuerdas
AL = 60p donde el diámetro AK = 120p.
y KL = 103;55p donde el diámetro AK = 120p.
por lo tanto donde AK = 1p, AL = 0;30p y KL = 0;52p.
Y, en las mismas unidades,
| KLD = 1210p | para la distancia del Sol | |
| KLD = 64;10p | para el primer límite de la Luna | [1 a] |
| KLD = 53;50p | para el segundo límite de la Luna | [1 b] |
| KLD = 43;53p | para el tercer límite de la Luna | [2 a] |
| KLD = 33;33p | para el cuarto límite de la Luna | [2 b] |
Y, por sustracción, LD [= KLD - KL], que es el mismo como AD, dado que la diferencia es imperceptible.
| En consecuencia AD = 1209;8p | para la distancia del Sol | |
| en consecuencia AD = 63;18p | para el primer límite de la Luna | [1 a] |
| en consecuencia AD = 52;58 | para el segundo límite de la Luna | [1 b] |
| en consecuencia AD = 43;1p | para el tercer límite de la Luna | [2 a] |
| en consecuencia AD = 32;41p | para el cuarto límite de la Luna | [2 b] |
Por lo tanto, donde la hipotenusa AD = 120p, entonces (asumiendo el mismo orden, para evitar la repetición)
| Sol | Luna | |||
|---|---|---|---|---|
| 1 a | 1 b | 2 a | 2 b | |
| AL = 0;2,59p | 0;56,52p | 1;7,58p | 1;23,41p | 1;50,9p |
Por lo tanto en el círculo alrededor del triángulo rectángulo DLA [3]
| Sol | Luna | |||
|---|---|---|---|---|
| 1 a | 1 b | 2 a | 2 b | |
| AL = 0;2,50º | 0;54,18º | 1;4,54º | alrededor de 1;20º | alrededor de 1;45º |
| Sol | Luna | |||
|---|---|---|---|---|
| 1 a | 1 b | 2 a | 2 b | |
| En consecuencia ^ ADB = ^ ZAΘ = 0;2,50ºº | 0;54,18ºº | 1;4,54ºº | 1;20ºº | 1;45ºº |
| donde 2 ángulos rectos = 360°° | ||||
| Sol | Luna | |||
|---|---|---|---|---|
| 1 a | 1 b | 2 a | 2 b | |
| En consecuencia ^ ADB = ^ ZAΘ = 0;1,25º | 0;27,9º | 0;32,27º | 0;40º [4] | 0;52,30º |
| donde 4 ángulos rectos = 360° | ||||
Entonces, dado que que el punto A es insignificantemente diferente desde el centro K, y el arco ZHΘ es insignificantemente mayor que el arco HΘ (toda la Tierra tiene la proporción [el tamaño] de un punto con [respecto] al círculo EZHΘ), en el círculo EZHΘ, el arco de la paralaje
| arco HΘ = 0;1,25º | para la distancia del Sol |
| arco HΘ= 0;27,9º | para el primer límite de la Luna |
| arco HΘ = 0;32,27º | para el segundo límite de la Luna |
| arco HΘ = 0;40º | para el tercer límite de la Luna |
| arco HΘ = 0;52,30º | para el cuarto límite de la Luna |
Lo que se ha requerido para examinar.
Por el mismo camino calculamos las paralajes de las otras distancias cenitales (a intervalos de 6º hasta los 90º del cuadrante) para cada límite, y construimos una tabla para determinar las paralajes. Nuevamente, la tabla tiene 45 líneas, y 9 columnas. En la primer columna ponemos los 90 grados del cuadrante, tabulándolos, obviamente, a intervalos de dos grados; en la segunda columna ponemos los minutos de la Paralaje Solar correspondiente a cada argumento, en la tercer columna la Paralaje Lunar en el primer límite; en la cuarta columna el incremento en la paralaje [lunar] en el segundo límite sobre el primer límite; en la quinta columna la paralaje [lunar] en el tercer límite; y en la sexta el incremento en la paralaje [lunar] en el cuarto límite sobre el tercer límite. Por lo tanto, por ejemplo, para un argumento de 30º ponemos 0;1,25º para el Sol, luego 0;27,9º para el primer límite de la Luna; seguido de 0;5,18º, que es el incremento del segundo límite sobre el primero; luego 0;40º, para el tercer límite, y seguido 0;12,30º, que es el incremento del cuarto límite sobre el tercero.
Necesitamos brindar un método conveniente para calcular la paralaje (correspondiente al argumento apropiado) para las distancias [de la Luna] en las posiciones intermedias entre el apogeo y el perigeo [de la excéntrica y del epiciclo], desde las paralajes tabuladas en los cuatro límites de arriba, utilizando minutos [de interpolación]. Para ello hemos añadido tres columnas restantes, para tomar en cuenta aquellas diferencias. Calculamos [los valores de] esas columnas de la siguiente manera.
Sea ABGD [Fig. 5.14] el epiciclo de la Luna con centro en E, y sea Z el centro de la Eclíptica y de la Tierra. Unir [ZE con una línea] AEDZ, dibujar ZGB, unir BE, GE, y eliminar las perpendiculares hasta AD, BH desde B, y GΘ desde G. Supongamos, primero, que el arco AB, la distancia de la Luna desde A, el apogeo verdadero [del epiciclo] tomado con respecto al centro Z, es de por ej. 60º.
En consecuencia ^ BEH = 60º donde 4 ángulos rectos = 360º
en consecuencia ^ BEH = 120ºº donde 2 ángulos rectos = 360ºº.

Por lo tanto en el círculo alrededor del triángulo rectángulo BEH
arco BH = 120º
y arco EH = 60º (suplementario).
Por lo tanto las cuerdas correspondientes
BH = 103;55p donde el diámetro EB = 120p.
y EH = 60p donde el diámetro EB = 120p.
Pero cuando centro E del epiciclo esta en el apogeo de la excéntrica,
ZE / EB = 60 / 5;15.
Por lo tanto, donde EB = 5;15p,
BH = 4;33p
EH = 2;38p
y, por adición [de EH a EZ], HEZ = 62;38p.
Y ZB² = ZH² + HB².
En consecuencia ZB = 62;48p, donde
la distancia al primer límite, ZA = 65;15p
la distancia al segundo límite, ZD = 54;45p
y la diferencia entre los dos límites, AD = 10;30p.
Por lo tanto la diferencia en B con respecto al primer límite es de [65;15 - 62;48 =] 2;27p donde la diferencia total es de 10;30p. En consecuencia donde la diferencia total es de 60p, la diferencia en B será de 14;0p. Entonces, estas [14;0p] es la cantidad que entraremos en la séptima columna sobre la línea [correspondiente al argumento] de la mitad del número 60, a saber 30. La razón de esto es que los 90 grados comprendidos en la primer columna de la tabla contiene la mitad de los 180 grados desde A a D [5].
Por el mismo razonamiento, si suponemos que el arco GD sea del mismo tamaño [como el arco AB de arriba], de 60º, será demostrado que
GΘ = 4;33p donde el radio EG = 5;15p.
y EΘ = 2;38p donde el radio EG = 5;15p.
Por lo tanto, por sustracción [de EΘ desde ZE], ZΘ = 57;22p. Por el mismo razonamiento [como el de arriba], la hipotenusa ZG = [(57;22² + 4;33²) ^ 0,5 =] 57;33p.
Nuevamente sustraemos esto [los 57;33p] desde las 65;15p del primer límite, y encontramos que el resultado, [es de] 7;42p, es 44;0 sexagésimas [partes] de la diferencia total. Esta será lo que entraremos en la misma [séptima] columna opuesta al argumento 60, dado que el arco ABG = 120º.
Con esos mismos arcos [AB y GD] como base, supongamos que el centro E esta en el perigeo de la excéntrica, que es la posición definiendo el tercer y cuarto límite. En esta posición
ZE / EB = 60;8 [6].
Por lo tanto donde BE = 8p, y asumiendo el arco AB y el arco GD como de 60º,
BH = GΘ = 6;56p donde ZE = 60p.
y EH = EΘ = 4;0p donde ZE = 60p.
En consecuencia ZH = [ZE + EH =] 64p
y ZΘ = [ZE - EH =] 56p,
entonces, por el mismo razonamiento [como el de arriba]
la hipotenusa ZB = [(ZH² + BH²) ^ 0,5 = ] 64;23p
y hipotenusa ZG = [(ZΘ² + GΘ²) ^ 0,5 = ] 56;26p,
donde [la distancia del] tercer límite, ZA = 68p,
y la diferencia entre el tercer y cuarto límite, [es de] AD = 16p.
Y 68p - 64;23p = 3;37p, que es la 13;33 sexagésima [parte] de la diferencia total, [igual a] 16p.
Entramos esta cantidad [de 13;33] en la octava columna opuesta al argumento 30, del mismo modo como antes.
También, 68p - 56;26p = 11;34p, que es la 43;24 sexagésima [parte] de la diferencia total, [de] 16p. Esta cantidad que entramos, similarmente en la octava columna opuesta al argumento 60.
Entonces, este es el camino por el que estableceremos las correcciones calculadas para el movimiento de la Luna sobre el epiciclo. Las correcciones para el movimiento del epiciclo sobre la excéntrica serán derivadas del siguiente modo.
Sea ABGD [Fig. 5.15] la excéntrica de la Luna con centro en E y el diámetro AEG, sobre el cuál Z es tomado como centro de la eclíptica. Dibujar BZD, y sean los ángulos AZB y GZD ambos, nuevamente, tomados [como] de 60º. Estas situaciones ocurren en elongaciones de 30º (cuando el centro del epiciclo esta en B), y 120º (cuando el centro del epiciclo esta en D). Unir BE, ED, y eliminar la perpendicular EH desde E hasta BZD.

Entonces, dado que el ^ BZA = 120ºº donde 2 ángulos rectos = 360ºº,
en el círculo alrededor el triángulo rectángulo EZH,
arco EH = 120º
y arco ZH = 60º (suplementario).
Por lo tanto las cuerdas correspondientes
EH = 103;55p donde la hipotenusa EZ = 120p.
y HZ = 60p donde la hipotenusa EZ = 120p.
Por lo tanto donde la distancia entre los centros, EZ = 10;19p
y el radio de la excéntrica es de 49;41p,
EH = 8;56p
y ZH = 5;10p.
Y dado que BH² = BE² - EH²,
BH = DH = 48;53p en las mismas unidades.
Por lo tanto, por adición [de ZH a BH], ZB = 54;3p,
y, por sustracción [de ZH desde DH], ZD = 43;43p.
donde [la distancia para] el primero [de los dos] límites, ZA = 60p
[la distancia para] el último [de los dos] límites, ZG = 39;22p
y la diferencia entre ellas = 20;38p.
Ahora 60p - 54;3p = 5;57p, que es la 17;18 sexagésima [parte] de la diferencia total de 20;38p;
y 60p - 43;43p = 16;17p, que es la 47;21 sexagésima [parte] de la diferencia total de 20;38p.
Por lo tanto, obviamente, entraremos las 17,18 [partes] en la novena columna opuesta al argumento de 30º de elongación, y las 47,21 opuestas [al argumento de] 120º, por ej. nuevamente opuesta a los 60º; dado que el perigeo [de la excéntrica] se ubica en los 90º [de elongación], una elongación de 60º es equivalente en distancia a una elongación de 120º.
Por el mismo camino calculamos los minutos [del coeficiente de interpolación] para las diferencias sobre los tres intervalos en cuestión para los otros arcos. Realizamos los cálculos a intervalos de 12º, que corresponden a 6º en los argumentos de la tabla, dado que los 180º desde el apogeo [del epiciclo o de la excéntrica] hasta el perigeo corresponden a los 90º [del argumento de la columna] en la tabla. Entramos esos minutos, calculados geométricamente, opuestos al argumento apropiado. Derivamos las entradas para los argumentos intermedios por interpolación lineal [7] sobre los intervalos de seis grados: la diferencia entre los resultados así derivados y los cálculos geométricos [precisos] son insignificantes sobre un intervalo pequeño, ambos para los minutos y para las presentes paralajes.
La tabla es la siguiente.
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Libro V |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 | 11 | 12 |
| 13 | 14 | 15 |
| 16 | 17 | 18 |
| 19 |
Notas de referencia
- ↑ Ver HAMA 112-15, Pedersen 213-17.
- ↑ En contraste a los componentes longitudinales y latitudinales de esta paralaje "total": éstas se tratan en el Libro V Capítulo 19.
- ↑ A partir de aquí Ptolomeo redondea drásticamente sus cálculos sobre el tercer y cuarto límite de la Luna. Su fundamento, sin lugar a dudas, es que en el cálculo de los eclipses solares (para lo cual la Tabla de la Paralaje esta principalmente diseñada) la Luna esta por definición cerca del apogeo de la excéntrica, y por lo tanto no hay ningún uso para el tercer y cuarto límite. Cf. Libro V Capítulo 18 nota de referencia nro. 1.
- ↑ Leer ο seg. μ (en el manuscrito D y en el Ar) en cambio de ο seg. μ ο (0;40,0) en H431,4 y en H431,13.
- ↑ La parte principal de la Tabla del Libro V Capítulo 18 (desde la 2° columna a la 6°) es una función de la Distancia Cenital, que varía entre 0º y 90º. No obstante, las columnas interpoladas 7 y 8 son una función de la anomalía α, que varía entre 0º y 180º. En orden de utilizar la misma columna como argumento para ambos [distancia cenital y anomalía], Ptolomeo tabula las columnas 7 y 8 como una función de ½ * α.
- ↑ Cf. Libro V Capítulo 7.
- ↑

Método de Interpolación por Lagrange. Click en la imagen para ampliar
Fórmula de interpolación solamente entre 2 pares de valores o puntos (X;Y), (i = 0 y 1 en Fórmula Polinómica de Lagrange).
α es el argumento a "entrar" en la columna de las X y el "Valor Interpolado" resulta de la columna de las Y.
Para una interpolación con más de 2 pares de valores (X;Y) verː Método de Interpolación por Lagrange, aunque para los valores que interpola Ptolomeo, con esta fórmula sencilla y reemplazándola con los 4 valores de una tabla, da el mismo resultado que el del astrónomo.
Nota del traductor al español.

